Double inclined cracks overlapping effect on mixed stress intensity factors using XFEM object-oriented implementation

Authors

DOI:

https://doi.org/10.15587/2706-5448.2024.298883

Keywords:

extended finite element method (XFEM), ), mixed mode stress intensity factor (MMSIF), inclined center crack, overlapping effect, C object-oriented programming

Abstract

The object of research is the Mixed Mode Stress Intensity Factor (MMSIF) of a two-dimensional (2D) plate.

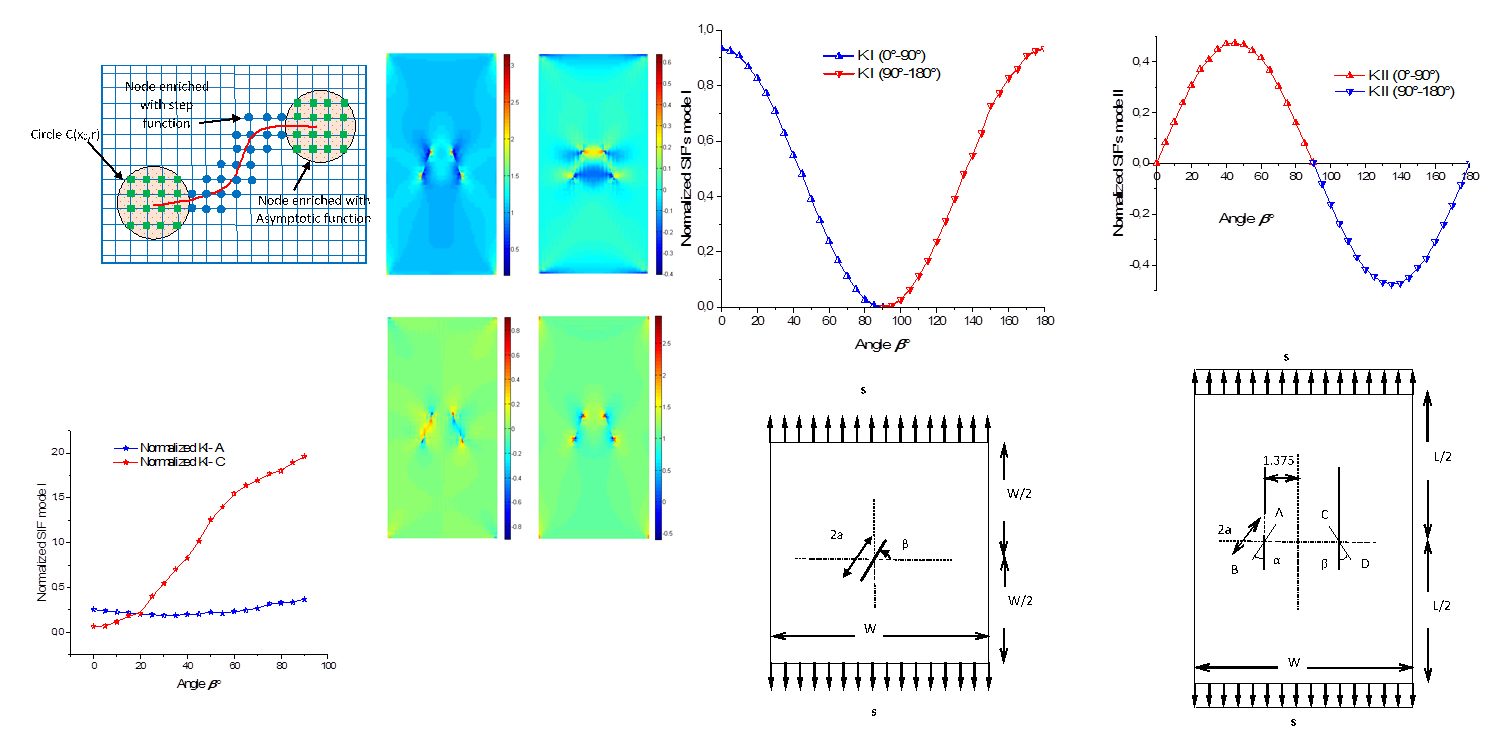
With the emergence of modern technologies and advanced innovations which contribute to the development and improvement of the design, implementation and management of construction projects, it has become easier. However, it is very difficult to manufacture components free from unavoidable defects, such as cracks, which lead to material deterioration and ultimately shorten its service life. Based on the process of local enrichment region using partition of unity concept, the extended finite element method (XFEM) has overcome the limitations of the standard FEM method in terms of modeling and numerical simulation of discontinuities (cracks) while gaining its general advantages. This makes XFEM a powerful and widely used digital tool in recent years. One of the most frequently raised problems in the discontinuities field (cracks) is the phenomenon of juxtaposition of multiple cracks in a cracked isotropic plate, which must be studied to determine the extent of its effect on the crack stress intensity factor in order to obtain higher safety reliability. On this basis, an improved object-oriented programming (OOP) with extended finite elements was used because of its great importance and well-known benefits.

In this paper, the MMSIF of a 2D plate is determined to show the effect of the out-of-phase orientation of the angle, as well as the effect of the juxtaposition of two inclined cracks. As a result of the research, it is shown that, the convergence between the results obtained in this study with those reported in the literature, and to theoretical values is remarkable, and their close agreement was noted. In the future, based on the object-oriented approach characteristics represented by flexibility, scalability, and modularity, which were explained in this research, this proposed approach can be enriched to include heterogeneous materials modeling, whether linear or nonlinear, crack propagation in dynamics, in addition to Complex 3D industrial problems.

Author Biographies

Rebadj Chabane, Laarbi Tébessi University

Postgraduate Student

Department of Civil Engineering

Mines Laboratory

Sabah Moussaoui, Sétif 1 University

Associate Professor

Department of Civil Engineering

Civil Engineering Research Laboratory

 

Mourad Belgasmia, Sétif 1 University

Professor

Department of Civil Engineering

Civil Engineering Research Laboratory

References

  1. Belytschko, T., Mos, N., Usui, S., Parimi, C. (2001). Arbitrary discontinuities in finite elements. International Journal for Numerical Methods in Engineering, 50 (4), 993–1013. doi: https://doi.org/10.1002/1097-0207(20010210)50:4<993::aid-nme164>3.0.co;2-m
  2. Belytschko, T., Gracie, R., Ventura, G. (2009). A review of extended/generalized finite element methods for material modeling. Modelling and Simulation in Materials Science and Engineering, 17 (4), 043001. doi: https://doi.org/10.1088/0965-0393/17/4/043001
  3. Belytschko, T., Gracie, R. (2007). On XFEM applications to dislocations and interfaces. International Journal of Plasticity, 23 (10-11), 1721–1738. doi: https://doi.org/10.1016/j.ijplas.2007.03.003
  4. Belytschko, T., Black, T. (1999). Elastic crack growth in finite elements with minimal remeshing. International Journal for Numerical Methods in Engineering, 45 (5), 601–620. doi: https://doi.org/10.1002/(sici)1097-0207(19990620)45:5<601::aid-nme598>3.0.co;2-s
  5. Mos, N., Dolbow, J., Belytschko, T. (1999). A finite element method for crack growth without remeshing. International Journal for Numerical Methods in Engineering, 46 (1), 131–150. doi: https://doi.org/10.1002/(sici)1097-0207(19990910)46:1<131::aid-nme726>3.0.co;2-j
  6. Moës, N., Belytschko, T. (2002). Extended finite element method for cohesive crack growth. Engineering Fracture Mechanics, 69 (7), 813–833. doi: https://doi.org/10.1016/s0013-7944(01)00128-x
  7. Parks, D. M. (1974). A stiffness derivative finite element technique for determination of crack tip stress intensity factors. International Journal of Fracture, 10 (4), 487–502. doi: https://doi.org/10.1007/bf00155252
  8. Hellen, T. K. (1975). On the method of virtual crack extensions. International Journal for Numerical Methods in Engineering, 9 (1), 187–207. doi: https://doi.org/10.1002/nme.1620090114
  9. Rybicki, E. F., Kanninen, M. F. (1977). A finite element calculation of stress intensity factors by a modified crack closure integral. Engineering Fracture Mechanics, 9 (4), 931–938. doi: https://doi.org/10.1016/0013-7944(77)90013-3
  10. Rice, J. R. (1968). A Path Independent Integral and the Approximate Analysis of Strain Concentration by Notches and Cracks. Journal of Applied Mechanics, 35 (2), 379–386. doi: https://doi.org/10.1115/1.3601206
  11. Rice, J. R., Rosengren, G. F. (1968). Plane strain deformation near a crack tip in a power-law hardening material. Journal of the Mechanics and Physics of Solids, 16 (1), 1–12. doi: https://doi.org/10.1016/0022-5096(68)90013-6
  12. Fracture mechanics. 19: San Antonio (1988). ASTM, Philadelphia, 939.
  13. Stern, M., Becker, E. B., Dunham, R. S. (1976). A contour integral computation of mixed-mode stress intensity factors. International Journal of Fracture, 12 (3), 359–368. doi: https://doi.org/10.1007/bf00032831
  14. Hedayati, E., Vahedi, M. (2014). Using Extended Finite Element Method for Computation of the Stress Intensity Factor, Crack Growth Simulation and Predicting Fatigue Crack Growth in a Slant-Cracked Plate of 6061-T651 Aluminum. World Journal of Mechanics, 4 (1), 24–30. doi: https://doi.org/10.4236/wjm.2014.41003
  15. Aliha, M. R. M., Bahmani, A., Akhondi, Sh. (2016). Mixed mode fracture toughness testing of PMMA with different three-point bend type specimens. European Journal of Mechanics – A/Solids, 58, 148–162. doi: https://doi.org/10.1016/j.euromechsol.2016.01.012
  16. Wang, Z., Yu, T., Bui, T. Q., Tanaka, S., Zhang, C., Hirose, S., Curiel-Sosa, J. L. (2017). 3-D local mesh refinement XFEM with variable-node hexahedron elements for extraction of stress intensity factors of straight and curved planar cracks. Computer Methods in Applied Mechanics and Engineering, 313, 375–405. doi: https://doi.org/10.1016/j.cma.2016.10.011
  17. Dimitri, R., Fantuzzi, N., Li, Y., Tornabene, F. (2017). Numerical computation of the crack development and SIF in composite materials with XFEM and SFEM. Composite Structures, 160, 468–490. doi: https://doi.org/10.1016/j.compstruct.2016.10.067
  18. Liao, Y., Zhang, X., Wang, B., He, M. (2023). Calculations of crack stress intensity factors based on FEM and XFEM models. Australian Journal of Mechanical Engineering, 1–11. doi: https://doi.org/10.1080/14484846.2023.2207243
  19. OpenXfem++. Available at: https://sourceforge.net/projects/openxfem/
  20. Khoei, A. R. (2015). Extended finite element method: theory and applications. Chichester: John Wiley & Sons, Inc, 584. doi: https://doi.org/10.1002/9781118869673
  21. Mohammadi, S. (2012). XFEM Fracture Analysis of Composites. Wiley. doi: https://doi.org/10.1002/9781118443378
  22. Khatri, K., Lal, A. (2019). Mixed mode stress intensity factors of slanted edge cracked plate with hole subjected to various in-plane loadings using XFEM. International Journal of Materials and Structural Integrity, 13 (1/2/3), 110. doi: https://doi.org/10.1504/ijmsi.2019.100388
  23. Laborde, P., Pommier, J., Renard, Y., Salaün, M. (2005). High-order extended finite element method for cracked domains. International Journal for Numerical Methods in Engineering, 64 (3), 354–381. doi: https://doi.org/10.1002/nme.1370
  24. Bordas, S., Nguyen, P. V., Dunant, C., Guidoum, A., Nguyen‐Dang, H. (2007). An extended finite element library. International Journal for Numerical Methods in Engineering, 71 (6), 703–732. doi: https://doi.org/10.1002/nme.1966
  25. Dubois-Pe`lerin, Y., Zimmermann, T. (1993). Object-oriented finite element programming: III. An efficient implementation in C++. Computer Methods in Applied Mechanics and Engineering, 108 (1-2), 165–183. doi: https://doi.org/10.1016/0045-7825(93)90159-u
  26. Sih, G. C., Paris, P. C., Erdogan, F. (1962). Crack-Tip, Stress-Intensity Factors for Plane Extension and Plate Bending Problems. Journal of Applied Mechanics, 29 (2), 306–312. doi: https://doi.org/10.1115/1.3640546
  27. Chen, W. H., Chen, T. C. (1995). An efficient dual boundary element technique for a two‐dimensional fracture problem with multiple cracks. International Journal for Numerical Methods in Engineering, 38 (10), 1739–1756. doi: https://doi.org/10.1002/nme.1620381009
Double inclined cracks overlapping effect on mixed stress intensity factors using XFEM object-oriented implementation12

Downloads

Published

2024-02-24

How to Cite

Chabane, R., Moussaoui, S., & Belgasmia, M. (2024). Double inclined cracks overlapping effect on mixed stress intensity factors using XFEM object-oriented implementation. Technology Audit and Production Reserves, 1(1(75), 12–18. https://doi.org/10.15587/2706-5448.2024.298883

Issue

Vol. 1 No. 1(75) (2024): Industrial and technology systems

Section

Mechanics

License

Copyright (c) 2024 Rebadj Chabane, Sabah Moussaoui, Mourad Belgasmia

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.