Development of high-speed algorithm for binomial arithmetic addition
DOI:
https://doi.org/10.15587/2706-5448.2024.301309Keywords:
binary binomial numbers, arithmetic addition, binomial arithmetic addition algorithms, dynamic arrayAbstract
The object of research is the method and algorithm of arithmetic addition of binomial numbers generated by binary binomial counting systems. The lack of binomial arithmetic, in particular the operation of adding binary binomial numbers, in a certain way prevents their introduction into information systems and the construction of information and communication technologies based on them for combinatorial optimization, generation of combinatorial objects, data compression and encryption.
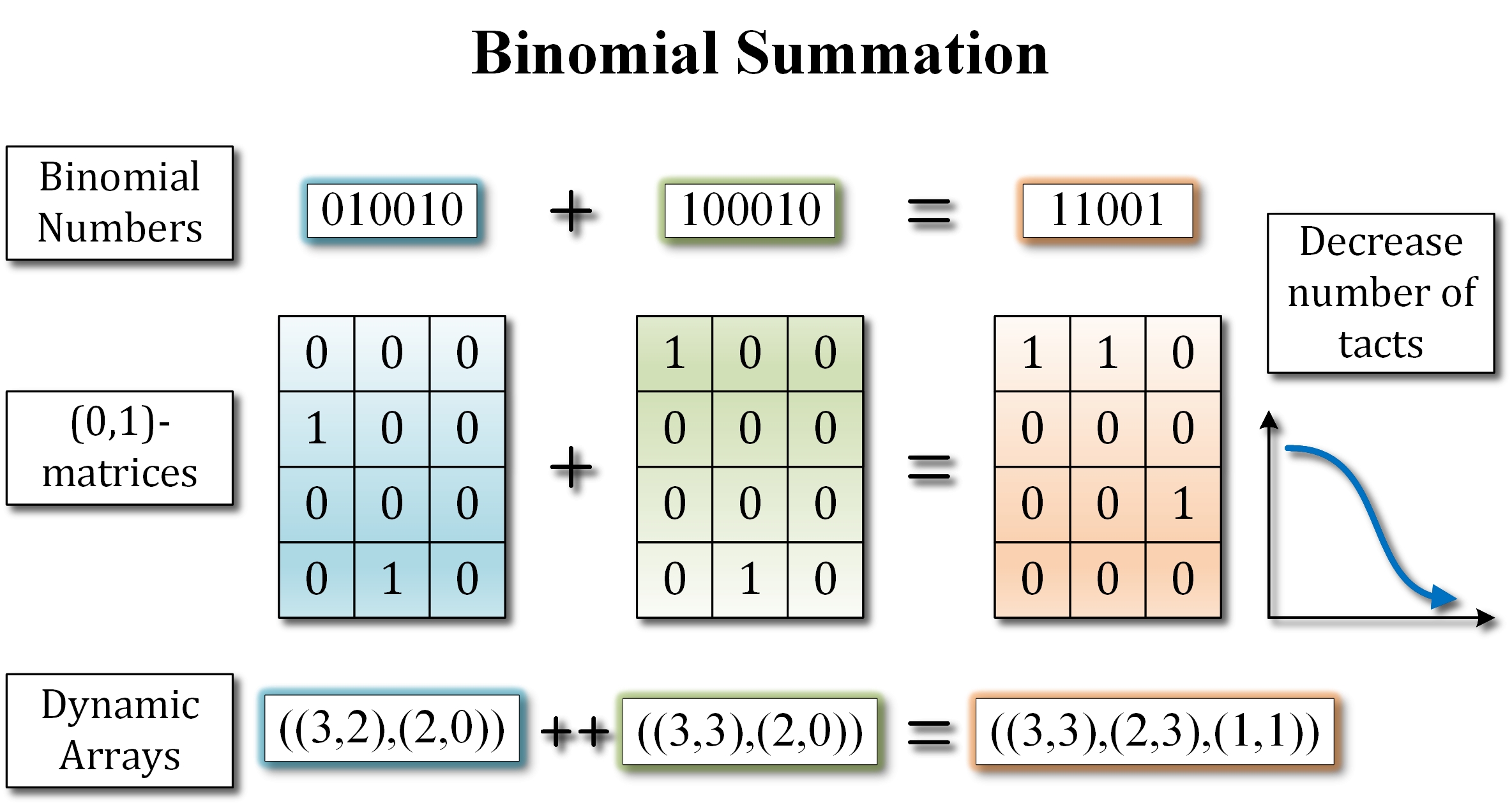
In the framework of the proposed approach, instead of operating with binomial coefficients, only operations with their upper and lower parameters are carried out. At the same time, the weighting coefficients of binary binomial numbers, which are added to each other, are represented in the form of two-component tuples. Taking this into account, this paper presents an algorithm for binomial arithmetic addition using dynamic arrays.
The main idea, which is included in the structure of the algorithm of binomial arithmetic addition based on dynamic arrays, is that the transition from a two-dimensional model of summation to a one-dimensional one is carried out. At the same time, only available, existing binomial coefficients are placed in the dynamic array. Accordingly, the search for binomial coefficients equal to or greater than the quantitative equivalent takes place in much smaller areas. In comparison with the algorithm based on matrix models, this quite significantly reduces the amount of time spent when performing the summation operation, and also reduces the requirements for the amount of memory required for placing two-component tuples of the assembly array.
In the course of the research, a several-fold decrease in the number of machine cycles required to search for the necessary elements in the dynamic array was practically confirmed. This leads to an increase in the performance of the presented algorithm of binomial arithmetic addition based on dynamic arrays. In turn, this leads to the acceleration of solving information tasks of combinatorial optimization, generation of combinatorial objects, data compression and encryption, for the solution of which the operation of adding binary binomial numbers is used.
References
- Stakhov, A. P. (2014). A History, the Main Mathematical Results and Applications for the Mathematics of Harmony. Applied Mathematics, 5 (3), 363–386. doi: https://doi.org/10.4236/am.2014.53039
- Borysenko, O. A. (2007). Chyslo i systemy chyslennia v elektronnykh tsyfrovykh systemakh. Visnyk SumDU, 4, 71–76.
- Butler, T. J., Tsutomu, S. (1997). Redundant Multiple-Valued Number Systems: Report. Defense Technical Information center. Naval Postgraduate School Monterey CA Dept of Electrical and Computer engineering, 10. Available at: https://apps.dtic.mil/sti/pdfs/ADA599946.pdf Last accessed: 10.02.2024
- Borisenko, A. A. (2004). Binomialnyi schet. Teoriia i praktika. Sumy: ITD «Universitetskaia kniga», 170.
- Mezmaz, M., Leroy, R., Melab, N., Tuyttens, D. (2014). A Multi-core Parallel Branch-and-Bound Algorithm Using Factorial Number System. 2014 IEEE 28th International Parallel and Distributed Processing Symposium. Phoenix, 1203–1212. doi: https://doi.org/10.1109/ipdps.2014.124
- Cui, X., Cui, X., Ni, Y., Miao, M., Yufeng, J. (2017). An Enhancement of Crosstalk Avoidance Code Based on Fibonacci Numeral System for Through Silicon Vias. IEEE Transactions on Very Large Scale Integration (VLSI) Systems, 25 (5), 1601–1610. doi: https://doi.org/10.1109/tvlsi.2017.2651141
- Borysenko, O., Matsenko, S., Bobrovs, V. (2021). Binomial Number System. Applied Sciences, 11 (23), 11110. doi: https://doi.org/10.3390/app112311110
- Kulik, І. A., Shevchenko, M. S., Grinenko, V. V. (2022). Algoritm skladannia dvіikovikh bіnomіalnikh chisel. Sistemi obrobki іnformatcіi, 2 (169), 49–57.
- Kulyk, I. A., Shevchenko, M. S. (2021). Matrychna model skladannia dviikovykh binomialnykh chysel. Systemy obrobky informatsii, 1 (164), 45–54.
- Anderson, Ja. A. (2001). Discrete mathematics with combinatorics. Prentice-Hall, Inc., 960.
Downloads
Published
How to Cite
Issue
Section
License
Copyright (c) 2024 Igor Kulyk, Maryna Shevchenko, Anatolii Melnyk, Tetyana Protasova

This work is licensed under a Creative Commons Attribution 4.0 International License.
The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.







