Внесок у мікромеханічне моделювання поширення зсувної хвилі в піщаному відкладенні
DOI:
https://doi.org/10.15587/2706-5448.2024.301709Ключові слова:
мікромеханічна модель, піщаний поклад, метод дискретних елементів, поширення зсувних хвильАнотація
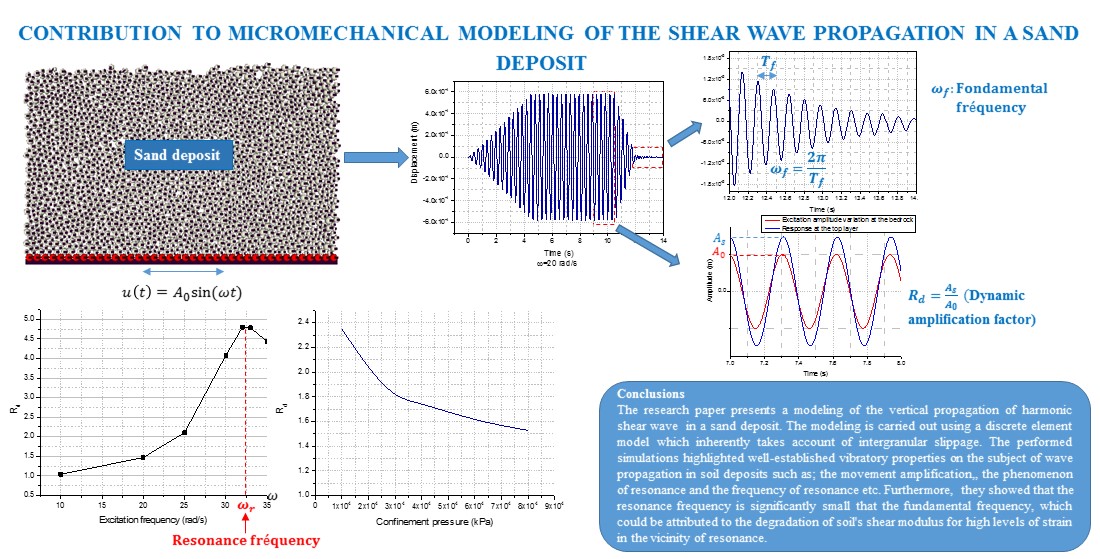
Об’єктом дослідження є поширення вертикальних хвиль у піщаному покладі. Ця стаття направлена на аналіз поширення вертикальних хвиль у піщаному покладі за допомогою мікромеханічного моделювання, яке враховує міжзернове ковзання під час деформації. Така задача, яка є частиною загальної теорії поширення хвиль у ґрунті, вже давно аналізується з використанням континуальних моделей, що базуються на наближених законах поведінки. Для цього розроблено 2D модель методу дискретних елементів (МДЕ). Модель МДЕ базується на молекулярній динаміці з використанням елементів круглої форми. Міжзеренні нормальні сили на контактах розраховуються за лінійним законом в'язкопружності, а дотичні сили – за ідеально пластичною в'язкопружною моделлю. Для врахування демпфування руху кочення зерен використовується модель тертя кочення. Реалізовано різні граничні умови профілю: корінна порода в основі, вільна поверхня вгорі та періодичні границі в горизонтальному напрямку. Піщаний поклад піддається гармонічному збудженню біля основи. Використовуючи цю модель, спочатку визначають основну та резонансну частоти покладу. Першу визначено з низькоамплітудних вільних коливань, а другу – шляхом проведення тесту зі змінною частотою збудження. Відзначено, що між цими двома частотами існує значний розрив, який можна пояснити деградацією модуля зсуву ґрунту поблизу резонансу. Така деградація добре доведена в класичній динаміці ґрунтів. Далі досліджено вплив висоти покладу та його залягання на резонансну частоту та коефіцієнт динамічного підсилення вільної поверхні. Отримані результати показали, що резонансна частота обернено пропорційна товщині покладу, тоді як коефіцієнт динамічного підсилення Rd зростає зі збільшенням товщини покладу. З іншого боку, зі збільшенням концентрації осад стає жорсткішим, що призводить до зменшення коефіцієнта підсилення. Такий результат узгоджується з теоретичними уявленнями про те, що найжорсткіші профілі, такі як гірські породи, не підсилюють сейсмічні рухи.
Посилання
- Jiang, M., Kamura, A., Kazama, M. (2022). Numerical study on liquefaction characteristics of granular materials under Rayleigh-wave strain conditions using 3D DEM. Soils and Foundations, 62 (4), 101176. doi: https://doi.org/10.1016/j.sandf.2022.101176
- Cui, J., Men, F., Wan, X. (2004). Soil liquefaction induced by Rayleigh wave. 13th World Conference on Earthquake Engineering.
- Nakase, H., Takeda, T., Oda, M. (1999). A simulation study on liquefaction using DEM. Proceedings of the 2nd International Conference on Earthquake Geotechnical Engineering, 637–642.
- Guo, Y., Zhao, C., Markine, V., Jing, G., Zhai, W. (2020). Calibration for discrete element modelling of railway ballast: A review. Transportation Geotechnics, 23. doi: https://doi.org/10.1016/j.trgeo.2020.100341
- Kumar, N., Suhr, B., Marschnig, S., Dietmaier, P., Marte, C., Six, K. (2019). Micromechanical investigation of railway ballast behavior under cyclic loading in a box test using DEM: Effects of elastic layers and ballast types. Granular Matter, 21, 106. doi: https://doi.org/10.1007/s10035-019-0956-9
- Zamani, N., El Shamy, U. (2011). Analysis of wave propagation in dry granular soils using DEM simulations. Acta Geotechnica, 6 (3), 167–182. doi: https://doi.org/10.1007/s11440-011-0142-7
- Sadd, M. H., Adhikari, G., Cardoso, F. (2000). DEM simulation of wave propagation in granular materials. Powder Technology, 109 Ž2000, 222–233. doi: https://doi.org/10.1016/s0032-5910(99)00238-7
- Sakamura, Y., Komaki, H. (2011). Numerical simulations of shock-induced load transfer processes in granular media using the discrete element method. Shock Waves, 22 (1), 57–68. doi: https://doi.org/10.1007/s00193-011-0347-6
- Ning, Z., Khoubani, A., Evans, T. M. (2015). Shear wave propagation in granular assemblies. Computers and Geotechnics, 69, 615–626. doi: https://doi.org/10.1016/j.compgeo.2015.07.004
- Tang, X., Yang, J. (2021). Wave propagation in granular material: What is the role of particle shape? Journal of the Mechanics and Physics of Solids, 157, 104605. doi: https://doi.org/10.1016/j.jmps.2021.104605
- Peters, J. F., Muthuswamy, M., Wibowo, J., Tordesillas, A. (2005). Characterization of force chains in granular material. Physical Review E, 72 (4). doi: https://doi.org/10.1103/physreve.72.041307
- Fu, L., Zhou, S., Guo, P., Wang, S., Luo, Z. (2019). Induced force chain anisotropy of cohesionless granular materials during biaxial compression. Granular Matter, 21 (3). doi: https://doi.org/10.1007/s10035-019-0899-1
- Fu, L., Zhou, S., Zheng, Y., Zhuang, L. (2023). Characterizing dynamic load propagation in cohesionless granular packing using force chain. Particuology, 81, 135–148. doi: https://doi.org/10.1016/j.partic.2023.01.007
- Campbell, C. S. (2003). A problem related to the stability of force chains. Granular Matter, 5 (3), 129–134. doi: https://doi.org/10.1007/s10035-003-0138-6
- Pöschel, T., Schwager, T. (2005). Computational Granular Dynamics – Models and Algorithms. Berlin, Heidelberg: Springer-Vrlag.
- Mansouri, M., El Youssoufi, M. S., Nicot, F. (2016). Numerical simulation of the quicksand phenomenon by a 3D coupled Discrete Element – Lattice Boltzmann hydromechanical model. International Journal for Numerical and Analytical Methods in Geomechanics, 41 (3), 338–358. doi: https://doi.org/10.1002/nag.2556
- Richefeu, V. (2005). Approche par éléments discrets 3D du comportement de matériaux granulaires cohésifs faiblement contraints. Thèse Université Montpellier II – Sciences et Techniques du Languedoc.
- Cundall, P. A., Strack, O. D. L. (1979) A discrete numerical model for granular assemblies. Géotechnique, 29 (1), 47–65. doi: https://doi.org/10.1680/geot.1979.29.1.47
- Delenne, J., El Youssoufi, M. S., Cherblanc, F., Bénet, J. (2004). Mechanical behaviour and failure of cohesive granular materials. International Journal for Numerical and Analytical Methods in Geomechanics, 28 (15), 1577–1594. doi: https://doi.org/10.1002/nag.401
- Semblat, J. F., Luong, M. P. (1998). Wave propagation through soils in centrifuge testing. Journal of Earthquake Engineering, 2 (10), 147–171. doi: https://doi.org/10.1080/13632469809350317
- Verruijt, A. (2009). An introduction to soil dynamics (Vol. 24). Springer Science & Business Media. doi: https://doi.org/10.1007/978-90-481-3441-0
- Acton, J. R., Squire, P. T. (1985) Solving Equations with Physical Understanding. Bristol: Adam Hilger Ltd., 219.
##submission.downloads##
Опубліковано
Як цитувати
Номер
Розділ
Ліцензія
Авторське право (c) 2024 Said Derbane, Mouloud Mansouri, Salah Messast

Ця робота ліцензується відповідно до Creative Commons Attribution 4.0 International License.
Закріплення та умови передачі авторських прав (ідентифікація авторства) здійснюється у Ліцензійному договорі. Зокрема, автори залишають за собою право на авторство свого рукопису та передають журналу право першої публікації цієї роботи на умовах ліцензії Creative Commons CC BY. При цьому вони мають право укладати самостійно додаткові угоди, що стосуються неексклюзивного поширення роботи у тому вигляді, в якому вона була опублікована цим журналом, але за умови збереження посилання на першу публікацію статті в цьому журналі.








