Reliability prediction of composite materials with random elastic inclusions

Authors

DOI:

https://doi.org/10.15587/2706-5448.2022.266411

Keywords:

elastic inclusions, composite materials failure, distribution function, statistical characteristics of strength, stochasticity of the structure

Abstract

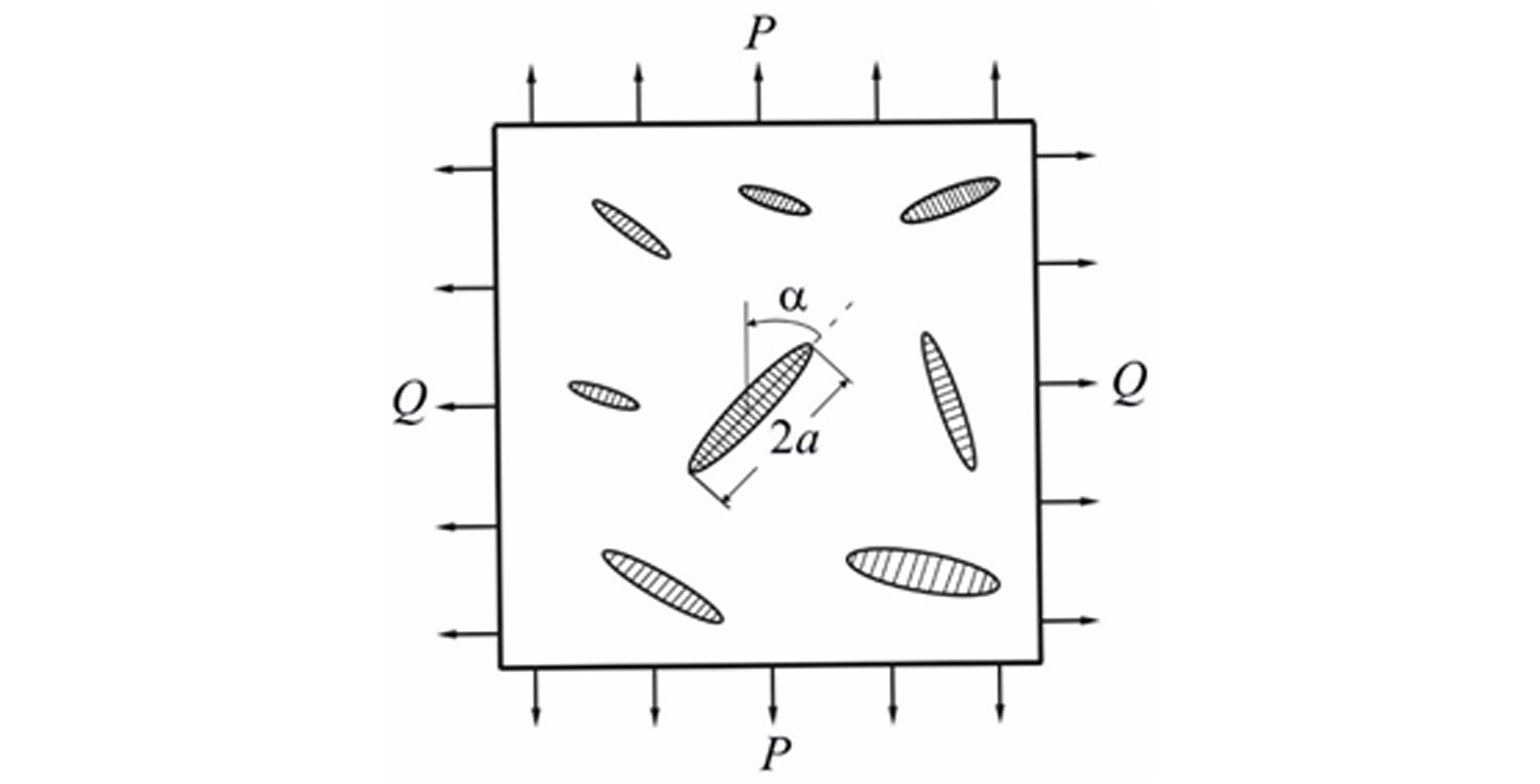
The object of the research is the construction of an algorithm that allows finding a number of strength (failure loading) statistical characteristics of a composite material plate under the conditions of a complex stress state. The relationships that determine the most probable value, mean value, dispersion and coefficient of variation of strength for an elastic homogeneous plate in which elliptical inclusions of another elastic material are uniformly distributed are written. Inclusions do not interact with each other and their geometric parameters are statistically independent random variables whose distribution laws are written for certain physical reasons.

The combination of the known deterministic solution of the composite materials failure theory and probabilistic statistical methods that take into account the randomness of the material structure makes it possible to study the failure of composite materials taking into account the stochasticity of their structure.

The main content of this article is the construction and analysis of the strength statistical characteristics algorithm of two-component lamellar composite materials. The mechanism of composite plate’s failure initiation in the inclusion is considered. The recorded relationships make it possible to calculate the most probable value, mean value, dispersion and coefficient of variation of strength and to investigate their dependence on the type of applied loading, structural heterogeneity of the composite and its dimensions (number of inclusions).

The obtained results allow effective assessment of the reliability of stochastically defective two-component composite structural materials under complex stress conditions. This is due to the fact that the combined consideration of defectiveness and randomness in the composite material structure as interconnected, inseparable phenomena open new opportunities for researching of the strength problem and failure of composite materials under various types of applied loading.

Author Biography

Roman Kvit, Lviv Polytechnic National University

PhD, Associate Professor

Department of Mathematics

References

  1. Chen, N.-Z., Guedes Soares, C. (2011). Ultimate strength and reliability of composite material structures. Marine Technology and Engineering. London: Taylor & Francis Group, 817–840.
  2. Kolios, A. J., Proia, S. (2012). Evaluation of the Reliability Performance of Failure Criteria for Composite Structures. World Journal of Mechanics, 02 (03), 162–170. doi: https://doi.org/10.4236/wjm.2012.23019
  3. Rypl, R., Chudoba, R., Scholzen, A., Vořechovský, M. (2013). Brittle matrix composites with heterogeneous reinforcement: Multi-scale model of a crack bridge with rigid matrix. Composites Science and Technology, 89, 98–109. doi: https://doi.org/10.1016/j.compscitech.2013.09.014
  4. Wang, F., Ding, J., Chen, Z. (2014). Statistical Analysis of the Progressive Failure Behavior for Fiber-Reinforced Polymer Composites under Tensile Loading. Polymers, 6 (1), 145–159. doi: https://doi.org/10.3390/polym6010145
  5. Liang, H., Li, S., Lu, Y., Yang, T. (2018). Reliability Study on FRP Composites Exposed to Wet-Dry Cycles. Applied Sciences, 8 (6), 892. doi: https://doi.org/10.3390/app8060892
  6. Naresh, K., Shankar, K., Velmurugan, R. (2018). Reliability analysis of tensile strengths using Weibull distribution in glass/epoxy and carbon/epoxy composites. Composites Part B: Engineering, 133, 129–144. doi: https://doi.org/10.1016/j.compositesb.2017.09.002
  7. Zhi, J., Tay, T.-E. (2020). Interrogating failure mechanisms of notched composites through a discrete crack modeling approach. Composites Science and Technology, 196, 108203. doi: https://doi.org/10.1016/j.compscitech.2020.108203
  8. Leong, K. H., Zhi, J., Lee, H. P., Tan, V. B. C., Tay, T. E. (2022). Adaptive multi-fidelity (AMF) modelling of progressive damage in notched composite laminates. Composites Part A: Applied Science and Manufacturing, 154, 106790. doi: https://doi.org/10.1016/j.compositesa.2021.106790
  9. Rakesh, P., More, A., Kumar, M., Muthu, N. (2022). Probabilistic failure prediction in a double composite cantilever beam with single and double source uncertainty. Composite Structures, 279, 114870. doi: https://doi.org/10.1016/j.compstruct.2021.114870
  10. Tan, W., Martínez-Pañeda, E. (2022). Phase field fracture predictions of microscopic bridging behaviour of composite materials. Composite Structures, 286, 115242. doi: https://doi.org/10.1016/j.compstruct.2022.115242
  11. Hardiman, N. J. (1954). Elliptic elastic inclusion in an infinite elastic plate. The Quarterly Journal of Mechanics and Applied Mathematics, 7 (2), 226–230. doi: https://doi.org/10.1093/qjmam/7.2.226
  12. Kvit, R. I. (2008). Statystychni kharakterystyky mitsnosti kompozytnykh materialiv za skladnoho napruzhenoho stanu. Visnyk Natsionalʹnoho universytetu «Lʹvivsʹka politekhnika». Fizyko-matematychni nauky, 625, 59–64.
  13. Baitsar, R., Kvit, R., Malyar, A. (2019). Statistical prediction of the reliability of composite materials with dispersive inclusions. ScienceRise, 2–3, 49–55. doi: https://doi.org/10.15587/2313-8416.2019.160880
  14. Cherepanov, G. P. (1983). Mekhanika razrusheniya kompozitsionnykh materialov. Nauka, 296.
  15. Vitvitskiy, P. M., Popina, S. Yu. (1980). Prochnost' i kriterii khrupkogo razrusheniya stokhasticheski defektnykh tel. Kyiv: Naukova dumka, 186.
  16. Pisarenko, G. S., Yakovlev, A. P., Matveyev, V. V.; Pisarenko, G. S. (Ed.) (1988). Spravochnik po soprotivleniyu materialov. Ed. 2. Kyiv: Naukova dumka, 736.
  17. Kvit, R. (2018). Strength statistical characteristics of the isotropic materials with disc-shaped defects. Journal of Applied Mathematics and Computational Mechanics, 17 (4), 25–34. doi: https://doi.org/10.17512/jamcm.2018.4.04
  18. Kvit, R. (2022). Development of the strength statistical characteristics of materials, which takes into account the features of their brittle fracture. Technology Audit and Production Reserves, 2 (1 (64)), 17–23. doi: https://doi.org/10.15587/2706-5448.2022.256569
  19. Gromov, G. V. (1975). Masshtabnyy effekt i statisticheskaya prochnost' materialov pri odnoosnom nagruzhenii. Voprosy nadezhnosti, dolgovechnosti i vosstanovleniya aviatsionnoy tekhniki, 2, 78–85.
  20. Freydental', A. M. (1975). Statisticheskiy podkhod k khrupkomu razrusheniyu. Razrusheniye, 2, 616–645.
Reliability prediction of composite materials with random elastic inclusions

Downloads

Published

2022-10-31

How to Cite

Kvit, R. (2022). Reliability prediction of composite materials with random elastic inclusions. Technology Audit and Production Reserves, 5(1(67), 11–17. https://doi.org/10.15587/2706-5448.2022.266411

Issue

Vol. 5 No. 1(67) (2022): Industrial and technology systems

Section

Materials Science: Reports on Research Projects

License

Copyright (c) 2022 Roman Kvit

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.