Прогнозування надійності композитних матеріалів з випадковими пружними включеннями
DOI:
https://doi.org/10.15587/2706-5448.2022.266411Ключові слова:
пружні включення, руйнування композитних матеріалів, функція розподілу, статистичні характеристики міцності, стохастичність структуриАнотація
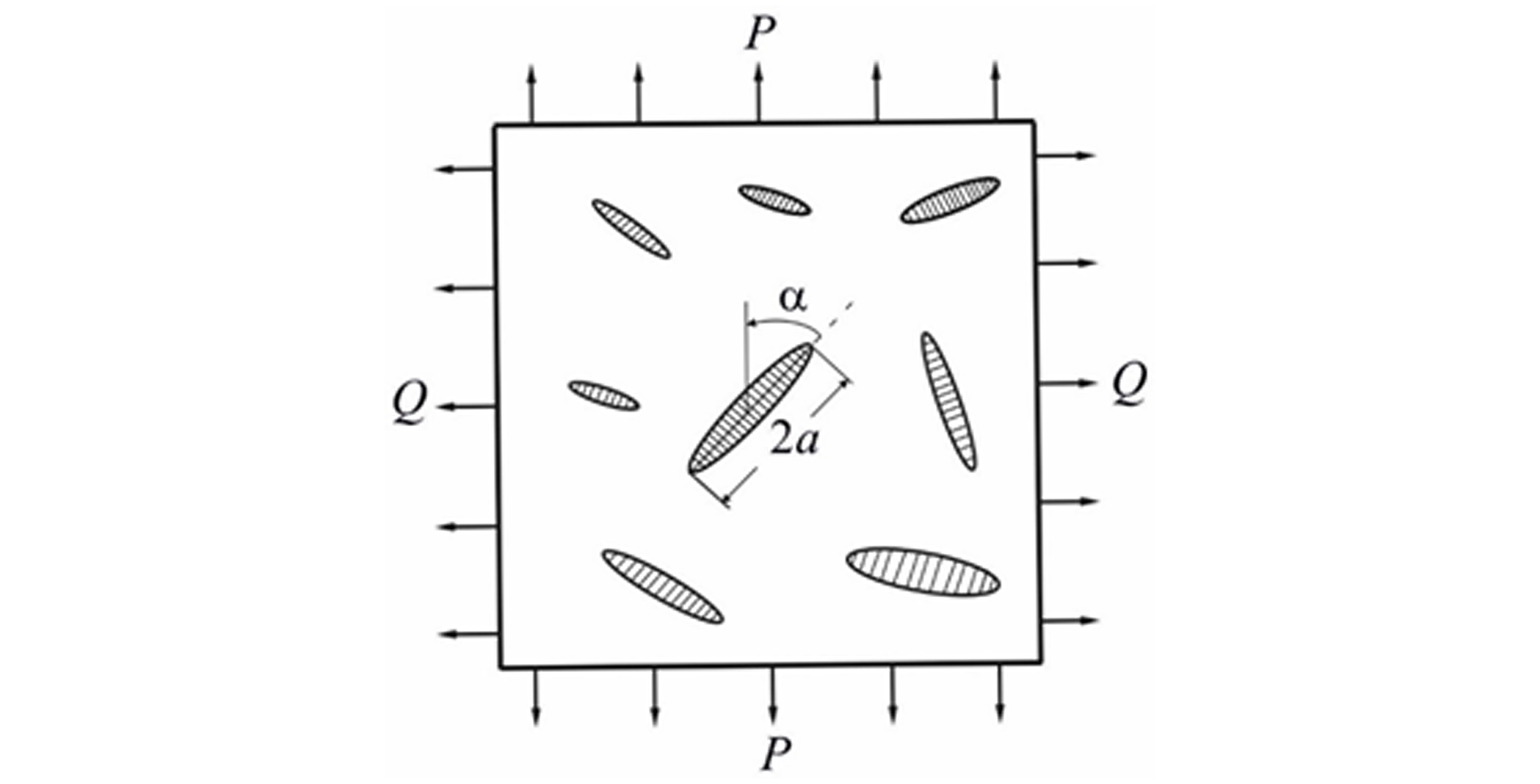
Об’єктом дослідження є побудова алгоритму, який дозволяє знаходити ряд статистичних характеристик міцності (руйнівного навантаження) пластини з композитного матеріалу за умов складного напруженого стану. Записано співвідношення, які визначають найімовірніше, середнє значення, дисперсію та коефіцієнт варіації міцності для пружної однорідної пластини, в якій рівномірно розподілені еліптичні включення з іншого пружного матеріалу. Включення не взаємодіють між собою та їх геометричні параметри є статистично незалежними випадковими величинами, закони розподілу яких записано з певних фізичних міркувань.
Поєднання відомого детерміністичного розв’язку теорії руйнування композитних матеріалів та ймовірнісно-статистичних методів, які враховують випадковість структури матеріалу, дає змогу провести дослідження руйнування композитних матеріалів із врахуванням стохастичності їх структури.
Основним змістом даної роботи є побудова та аналіз алгоритму статистичних характеристик міцності двокомпонентних пластинчатих композитних матеріалів. Розглянуто механізм початку руйнування композитних пластин у включенні. Записані співвідношення дають змогу обчислити найімовірніше, середнє значення та коефіцієнт варіації міцності та дослідити їх залежність від виду прикладеного навантаження, структурної неоднорідності композита та його розмірів (кількості включень).
Отримані результати дозволяють здійснити ефективну оцінку надійності стохастисно дефектних двокомпонентних композитних конструкційних матеріалів за умов складного напруженого стану. Це пов’язано з тим, що сумісне врахування дефектності та випадковості в структурі композитного матеріалу як взаємозв’язаних, невід’ємних явищ відкриває нові можливості для дослідження проблеми міцності та руйнування композитних матеріалів за різних видів прикладеного навантаження.
Посилання
- Chen, N.-Z., Guedes Soares, C. (2011). Ultimate strength and reliability of composite material structures. Marine Technology and Engineering. London: Taylor & Francis Group, 817–840.
- Kolios, A. J., Proia, S. (2012). Evaluation of the Reliability Performance of Failure Criteria for Composite Structures. World Journal of Mechanics, 02 (03), 162–170. doi: https://doi.org/10.4236/wjm.2012.23019
- Rypl, R., Chudoba, R., Scholzen, A., Vořechovský, M. (2013). Brittle matrix composites with heterogeneous reinforcement: Multi-scale model of a crack bridge with rigid matrix. Composites Science and Technology, 89, 98–109. doi: https://doi.org/10.1016/j.compscitech.2013.09.014
- Wang, F., Ding, J., Chen, Z. (2014). Statistical Analysis of the Progressive Failure Behavior for Fiber-Reinforced Polymer Composites under Tensile Loading. Polymers, 6 (1), 145–159. doi: https://doi.org/10.3390/polym6010145
- Liang, H., Li, S., Lu, Y., Yang, T. (2018). Reliability Study on FRP Composites Exposed to Wet-Dry Cycles. Applied Sciences, 8 (6), 892. doi: https://doi.org/10.3390/app8060892
- Naresh, K., Shankar, K., Velmurugan, R. (2018). Reliability analysis of tensile strengths using Weibull distribution in glass/epoxy and carbon/epoxy composites. Composites Part B: Engineering, 133, 129–144. doi: https://doi.org/10.1016/j.compositesb.2017.09.002
- Zhi, J., Tay, T.-E. (2020). Interrogating failure mechanisms of notched composites through a discrete crack modeling approach. Composites Science and Technology, 196, 108203. doi: https://doi.org/10.1016/j.compscitech.2020.108203
- Leong, K. H., Zhi, J., Lee, H. P., Tan, V. B. C., Tay, T. E. (2022). Adaptive multi-fidelity (AMF) modelling of progressive damage in notched composite laminates. Composites Part A: Applied Science and Manufacturing, 154, 106790. doi: https://doi.org/10.1016/j.compositesa.2021.106790
- Rakesh, P., More, A., Kumar, M., Muthu, N. (2022). Probabilistic failure prediction in a double composite cantilever beam with single and double source uncertainty. Composite Structures, 279, 114870. doi: https://doi.org/10.1016/j.compstruct.2021.114870
- Tan, W., Martínez-Pañeda, E. (2022). Phase field fracture predictions of microscopic bridging behaviour of composite materials. Composite Structures, 286, 115242. doi: https://doi.org/10.1016/j.compstruct.2022.115242
- Hardiman, N. J. (1954). Elliptic elastic inclusion in an infinite elastic plate. The Quarterly Journal of Mechanics and Applied Mathematics, 7 (2), 226–230. doi: https://doi.org/10.1093/qjmam/7.2.226
- Kvit, R. I. (2008). Statystychni kharakterystyky mitsnosti kompozytnykh materialiv za skladnoho napruzhenoho stanu. Visnyk Natsionalʹnoho universytetu «Lʹvivsʹka politekhnika». Fizyko-matematychni nauky, 625, 59–64.
- Baitsar, R., Kvit, R., Malyar, A. (2019). Statistical prediction of the reliability of composite materials with dispersive inclusions. ScienceRise, 2–3, 49–55. doi: https://doi.org/10.15587/2313-8416.2019.160880
- Cherepanov, G. P. (1983). Mekhanika razrusheniya kompozitsionnykh materialov. Nauka, 296.
- Vitvitskiy, P. M., Popina, S. Yu. (1980). Prochnost' i kriterii khrupkogo razrusheniya stokhasticheski defektnykh tel. Kyiv: Naukova dumka, 186.
- Pisarenko, G. S., Yakovlev, A. P., Matveyev, V. V.; Pisarenko, G. S. (Ed.) (1988). Spravochnik po soprotivleniyu materialov. Ed. 2. Kyiv: Naukova dumka, 736.
- Kvit, R. (2018). Strength statistical characteristics of the isotropic materials with disc-shaped defects. Journal of Applied Mathematics and Computational Mechanics, 17 (4), 25–34. doi: https://doi.org/10.17512/jamcm.2018.4.04
- Kvit, R. (2022). Development of the strength statistical characteristics of materials, which takes into account the features of their brittle fracture. Technology Audit and Production Reserves, 2 (1 (64)), 17–23. doi: https://doi.org/10.15587/2706-5448.2022.256569
- Gromov, G. V. (1975). Masshtabnyy effekt i statisticheskaya prochnost' materialov pri odnoosnom nagruzhenii. Voprosy nadezhnosti, dolgovechnosti i vosstanovleniya aviatsionnoy tekhniki, 2, 78–85.
- Freydental', A. M. (1975). Statisticheskiy podkhod k khrupkomu razrusheniyu. Razrusheniye, 2, 616–645.
##submission.downloads##
Опубліковано
Як цитувати
Номер
Розділ
Ліцензія
Авторське право (c) 2022 Roman Kvit

Ця робота ліцензується відповідно до Creative Commons Attribution 4.0 International License.
Закріплення та умови передачі авторських прав (ідентифікація авторства) здійснюється у Ліцензійному договорі. Зокрема, автори залишають за собою право на авторство свого рукопису та передають журналу право першої публікації цієї роботи на умовах ліцензії Creative Commons CC BY. При цьому вони мають право укладати самостійно додаткові угоди, що стосуються неексклюзивного поширення роботи у тому вигляді, в якому вона була опублікована цим журналом, але за умови збереження посилання на першу публікацію статті в цьому журналі.








