A study of mesh influence on extended finite element cracked plate and finite element plate bending

Authors

DOI:

https://doi.org/10.15587/2706-5448.2023.274348

Keywords:

extended finite element method (XFEM), finite element method (FEM), crack, transient analysis, plate

Abstract

The object of this study is a refining mesh effect on discontinuous structures response.

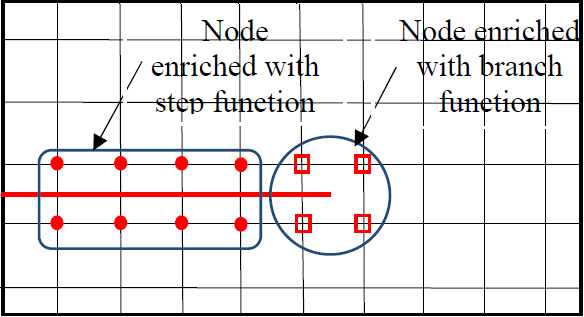
This paper presents a study of mesh influence between cracked and non-cracked plates using extended finite element and standard finite element method, respectively. For the first case, the plate is stressed on one side, in which cracked zone displacements are given for different mesh refinements. The second case study is bending orthotropic and isotropic plates under uniform rectangular impulsive load, in which mesh influence on the structural response is presented. The numerical modelization is done using an isoperimetric quadrilateral element. On one hand, the stiffness linear matrix of a cracked plate is evaluated numerically by adding an enriched shape function to the standard shape function to be able to model discontinuity numerically. On the other hand, for the case of the non-cracked plate, the use of the finite element method with standard shape function is well suited to the numerical design of stiffness and mass matrix.

The essence of this study is to show the mesh effect on cracked and non-craked plate response, which is a first step that allows to go even further on monoitoring of our crack evolution.It is a very useful field as any structure in our daily life is subject to a discontinuity (crack) which we must be able to control in order to evoid a future structure collapse.

Supporting Agency

  • Presentation of research in the form of publication through financial support in the form of a grant from SUES (Support to Ukrainian Editorial Staff).

Author Biographies

Sabah Moussaoui, Sétif 1 University

PhD

Department of Civil Engineering

Chabane Rebadj, Laarbi Tébessi University

Postgraduate Student

Department of Civil Engineering

Mourad Belgasmia, Sétif 1 University

Professor

Department of Civil Engineering

Kong Fah Tee, INTI International University

Professor

Faculty of Engineering and Quantity Surveying

 

References

  1. Belytschko, T., Black, T. (1999). Elastic crack growth in finite elements with minimal remeshing. International Journal for Numerical Methods in Engineering, 45 (5), 601–620. doi: https://doi.org/10.1002/(sici)1097-0207(19990620)45:5<601::aid-nme598>3.0.co;2-s
  2. Zi, G., Belytschko, T. (2003). New crack-tip elements for XFEM and applications to cohesive cracks. International Journal for Numerical Methods in Engineering, 57 (15), 2221–2240. doi: https://doi.org/10.1002/nme.849
  3. Moes, N., Dolbow, J., Belytschko, T. (1999). A finite element method for crack growth without remeshing. International Journal for Numerical Methods in Engineering, 46 (1), 131–150. doi: https://doi.org/10.1002/(sici)1097-0207(19990910)46:1<131::aid-nme726>3.0.co;2-j
  4. Khoei, A. R. (2015). Extended finite element method: theory and applications. Chichester: John Wiley & Sons, Inc, 584.
  5. Sukumar, N., Prévost, J.-H. (2003). Modeling quasi-static crack growth with the extended finite element method Part I: Computer implementation. International Journal of Solids and Structures, 40 (26), 7513–7537. doi: https://doi.org/10.1016/j.ijsolstr.2003.08.002
  6. Nagashima, T., Wang, C. (2021). XFEM Analyses Using Two-Dimensional Quadrilateral Elements Enriched with Only the Heaviside Step Function. International Journal of Computational Methods, 19 (2). doi: https://doi.org/10.1142/s0219876221500638
  7. Bansal, M., Singh, I. V., Mishra, B. K., Bordas, S. P. A. (2019). A parallel and efficient multi-split XFEM for 3-D analysis of heterogeneous materials. Computer Methods in Applied Mechanics and Engineering, 347, 365–401. doi: https://doi.org/10.1016/j.cma.2018.12.023
  8. Agathos, K., Chatzi, E., Bordas, S. P. A. (2018). Multiple crack detection in 3D using a stable XFEM and global optimization. Computational Mechanics, 62 (4), 835–852. doi: https://doi.org/10.1007/s00466-017-1532-y
  9. Ding, J., Yu, T., Bui, T. Q. (2020). Modeling strong/weak discontinuities by local mesh refinement variable-node XFEM with object-oriented implementation. Theoretical and Applied Fracture Mechanics, 106, 102434. doi: https://doi.org/10.1016/j.tafmec.2019.102434
  10. Moës, N., Belytschko, T. (2002). Extended finite element method for cohesive crack growth. Engineering Fracture Mechanics, 69 (7), 813–833. doi: https://doi.org/10.1016/s0013-7944(01)00128-x
  11. Dunant, C., Vinh, P. N., Belgasmia, M., Bordas, S., Guidoum, A. (2007). Architecture tradeoffs of integrating a mesh generator to partition of unity enriched object-oriented finite element software. European Journal of Computational Mechanics, 16 (2), 237–258. doi: https://doi.org/10.3166/remn.16.237-258
  12. Rustum Mohsin, N., Shekher Jabur, L. (2019). Stress intensity factor for double edge cracked finite plate subjected to tensile stress. University of Thi-Qar Journal for Engineering Sciences, 7 (1), 101–115.
  13. Sharma, K. (2014). Crack Interaction Studies Using XFEM Technique. Journal of Solid Mechanics, 6 (4), 410–421.
  14. Jabur, L. S. (2015). Theorical and numerical analysis of central crack plate with different orientation under tensile load. International Journal for Industrial Engineering and technology, 2278–9456.
  15. Dolbow, J., Moës, N., Belytschko, T. (2000). Modeling fracture in Mindlin–Reissner plates with the extended finite element method. International Journal of Solids and Structures, 37 (48-50), 7161–7183. doi: https://doi.org/10.1016/s0020-7683(00)00194-3
  16. Hughes, T. J. R. (2000). The finite element method: linear static and dynamic finite element analysis. Mineola: Dover Publications, 704.
  17. Clough, R. W., Penzien, J., Claudon, J.-L. (1980). Dynamique des structures. Paris: Éditions Pluralis, 752.
  18. Belgasmia, M. (2021). Structural dynamics and static nonlinear analysis from theory to application. Engineering Science Reference, an imprint of IGI Global. Hershey, 347.
  19. Smith, I. M., Griffiths, D. V., Margetts, L. (2014). Programming the finite element method. Chichester, John Wiley & Sons Inc, 684.
  20. Bhatt, P. (2002). Programming the Dynamic Analysis of Structures. CRC Press, 464.
A study of mesh influence on extended finite element cracked plate and finite element plate bending

Downloads

Published

2023-02-24

How to Cite

Moussaoui, S., Rebadj, C., Belgasmia, M., & Tee, K. F. (2023). A study of mesh influence on extended finite element cracked plate and finite element plate bending. Technology Audit and Production Reserves, 1(1(69), 6–12. https://doi.org/10.15587/2706-5448.2023.274348

Issue

Vol. 1 No. 1(69) (2023): Industrial and technology systems

Section

Mechanics

License

Copyright (c) 2023 Sabah Moussaoui, Chabane Rebadj, Mourad Belgasmia, Kong Fah Tee

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.