Дослідження впливу сітки на розтягнуту пластину з тріщинами та вигин кінцево-елементної пластини

Автор(и)

DOI:

https://doi.org/10.15587/2706-5448.2023.274348

Ключові слова:

розширений метод скінченних елементів (РМСЕ), метод скінченних елементів (МСЕ), тріщина, перехідний аналіз, пластина

Анотація

Об’єктом цього дослідження є вплив роздрібнюючої сітки на реакцію розривних структур.

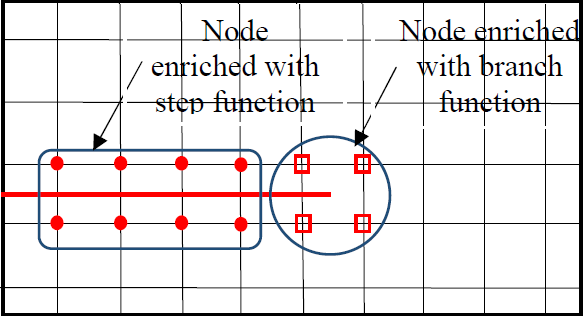
У цій роботі представлено дослідження впливу сітки між пластинами з тріщинами та без тріщин за допомогою розширеного методу кінцевих елементів та стандартного методу кінцевих елементів відповідно. У першому випадку пластина напружена з одного боку, в якому задані переміщення зони тріщин для різних розмірів сітки. Другий приклад – вигин ортотропних та ізотропних пластин під однорідним прямокутним імпульсним навантаженням, у якому представлено вплив сітки на структурну реакцію. Чисельне моделювання виконано з використанням ізопериметричного чотирикутного елемента. З одного боку, лінійна матриця жорсткості пластини з тріщинами оцінюється чисельно шляхом додавання збагаченої функції форми до стандартної функції форми, щоб мати можливість чисельно моделювати розрив. З іншого боку, для випадку пластини без тріщин використання методу кінцевих елементів зі стандартною функцією форми добре підходить для чисельного проєктування матриці жорсткості та маси.

Суть цього дослідження полягає в тому, щоб показати вплив сітки на реакцію пластини з тріщинами та без тріщин, що є першим кроком, який дозволяє нам піти ще далі в моніторингу розвитку нашої тріщини.

Це дужий корисний напрямок, оскільки будь-яка структура в нашому повсякденному житті піддається розриву (тріщині), який ми повинні мати можливість контролювати, щоб уникнути майбутнього колапсу структури.

Спонсор дослідження

  • Presentation of research in the form of publication through financial support in the form of a grant from SUES (Support to Ukrainian Editorial Staff).

Біографії авторів

Sabah Moussaoui, Sétif 1 University

PhD

Department of Civil Engineering

Chabane Rebadj, Laarbi Tébessi University

Postgraduate Student

Department of Civil Engineering

Mourad Belgasmia, Sétif 1 University

Professor

Department of Civil Engineering

Kong Fah Tee, INTI International University

Professor

Faculty of Engineering and Quantity Surveying

 

Посилання

  1. Belytschko, T., Black, T. (1999). Elastic crack growth in finite elements with minimal remeshing. International Journal for Numerical Methods in Engineering, 45 (5), 601–620. doi: https://doi.org/10.1002/(sici)1097-0207(19990620)45:5<601::aid-nme598>3.0.co;2-s
  2. Zi, G., Belytschko, T. (2003). New crack-tip elements for XFEM and applications to cohesive cracks. International Journal for Numerical Methods in Engineering, 57 (15), 2221–2240. doi: https://doi.org/10.1002/nme.849
  3. Moes, N., Dolbow, J., Belytschko, T. (1999). A finite element method for crack growth without remeshing. International Journal for Numerical Methods in Engineering, 46 (1), 131–150. doi: https://doi.org/10.1002/(sici)1097-0207(19990910)46:1<131::aid-nme726>3.0.co;2-j
  4. Khoei, A. R. (2015). Extended finite element method: theory and applications. Chichester: John Wiley & Sons, Inc, 584.
  5. Sukumar, N., Prévost, J.-H. (2003). Modeling quasi-static crack growth with the extended finite element method Part I: Computer implementation. International Journal of Solids and Structures, 40 (26), 7513–7537. doi: https://doi.org/10.1016/j.ijsolstr.2003.08.002
  6. Nagashima, T., Wang, C. (2021). XFEM Analyses Using Two-Dimensional Quadrilateral Elements Enriched with Only the Heaviside Step Function. International Journal of Computational Methods, 19 (2). doi: https://doi.org/10.1142/s0219876221500638
  7. Bansal, M., Singh, I. V., Mishra, B. K., Bordas, S. P. A. (2019). A parallel and efficient multi-split XFEM for 3-D analysis of heterogeneous materials. Computer Methods in Applied Mechanics and Engineering, 347, 365–401. doi: https://doi.org/10.1016/j.cma.2018.12.023
  8. Agathos, K., Chatzi, E., Bordas, S. P. A. (2018). Multiple crack detection in 3D using a stable XFEM and global optimization. Computational Mechanics, 62 (4), 835–852. doi: https://doi.org/10.1007/s00466-017-1532-y
  9. Ding, J., Yu, T., Bui, T. Q. (2020). Modeling strong/weak discontinuities by local mesh refinement variable-node XFEM with object-oriented implementation. Theoretical and Applied Fracture Mechanics, 106, 102434. doi: https://doi.org/10.1016/j.tafmec.2019.102434
  10. Moës, N., Belytschko, T. (2002). Extended finite element method for cohesive crack growth. Engineering Fracture Mechanics, 69 (7), 813–833. doi: https://doi.org/10.1016/s0013-7944(01)00128-x
  11. Dunant, C., Vinh, P. N., Belgasmia, M., Bordas, S., Guidoum, A. (2007). Architecture tradeoffs of integrating a mesh generator to partition of unity enriched object-oriented finite element software. European Journal of Computational Mechanics, 16 (2), 237–258. doi: https://doi.org/10.3166/remn.16.237-258
  12. Rustum Mohsin, N., Shekher Jabur, L. (2019). Stress intensity factor for double edge cracked finite plate subjected to tensile stress. University of Thi-Qar Journal for Engineering Sciences, 7 (1), 101–115.
  13. Sharma, K. (2014). Crack Interaction Studies Using XFEM Technique. Journal of Solid Mechanics, 6 (4), 410–421.
  14. Jabur, L. S. (2015). Theorical and numerical analysis of central crack plate with different orientation under tensile load. International Journal for Industrial Engineering and technology, 2278–9456.
  15. Dolbow, J., Moës, N., Belytschko, T. (2000). Modeling fracture in Mindlin–Reissner plates with the extended finite element method. International Journal of Solids and Structures, 37 (48-50), 7161–7183. doi: https://doi.org/10.1016/s0020-7683(00)00194-3
  16. Hughes, T. J. R. (2000). The finite element method: linear static and dynamic finite element analysis. Mineola: Dover Publications, 704.
  17. Clough, R. W., Penzien, J., Claudon, J.-L. (1980). Dynamique des structures. Paris: Éditions Pluralis, 752.
  18. Belgasmia, M. (2021). Structural dynamics and static nonlinear analysis from theory to application. Engineering Science Reference, an imprint of IGI Global. Hershey, 347.
  19. Smith, I. M., Griffiths, D. V., Margetts, L. (2014). Programming the finite element method. Chichester, John Wiley & Sons Inc, 684.
  20. Bhatt, P. (2002). Programming the Dynamic Analysis of Structures. CRC Press, 464.
A study of mesh influence on extended finite element cracked plate and finite element plate bending

##submission.downloads##

Опубліковано

2023-02-24

Як цитувати

Moussaoui, S., Rebadj, C., Belgasmia, M., & Tee, K. F. (2023). Дослідження впливу сітки на розтягнуту пластину з тріщинами та вигин кінцево-елементної пластини. Technology Audit and Production Reserves, 1(1(69), 6–12. https://doi.org/10.15587/2706-5448.2023.274348

Номер

Том 1 № 1(69) (2023): Виробничо-технологічні системи

Розділ

Механіка

Ліцензія

Авторське право (c) 2023 Sabah Moussaoui, Chabane Rebadj, Mourad Belgasmia, Kong Fah Tee

Creative Commons License

Ця робота ліцензується відповідно до Creative Commons Attribution 4.0 International License.

Закріплення та умови передачі авторських прав (ідентифікація авторства) здійснюється у Ліцензійному договорі. Зокрема, автори залишають за собою право на авторство свого рукопису та передають журналу право першої публікації цієї роботи на умовах ліцензії Creative Commons CC BY. При цьому вони мають право укладати самостійно додаткові угоди, що стосуються неексклюзивного поширення роботи у тому вигляді, в якому вона була опублікована цим журналом, але за умови збереження посилання на першу публікацію статті в цьому журналі.