Higher order dispersions effect on high-order soliton interactions

Authors

DOI:

https://doi.org/10.15587/2706-5448.2023.277346

Keywords:

higher order solitons, soliton fission, dispersions, nonlinearity, optical fiber, supercontinuum

Abstract

The object of the research is deleting the interaction of the higher order soliton interaction by introducing the third and fourth order dispersions inside an optical fiber. The results are obtained by the simulation of the nonlinear Schrödinger equation, which models the propagation of solitons in the optical fiber using the method of Fast Fourier Transform.

The interaction of two higher order solitons due to the attraction of their electric field can lead to losing the solitons' properties. Hence, this can prevent the use of solitons in high-bit-rate optical fiber communication systems because it increases the bit error rate, significantly limiting the potential of the communication system. To resolve this problem, we should diminish the bit rate error by avoiding the interaction of the co-propagative solitons when they are too close.

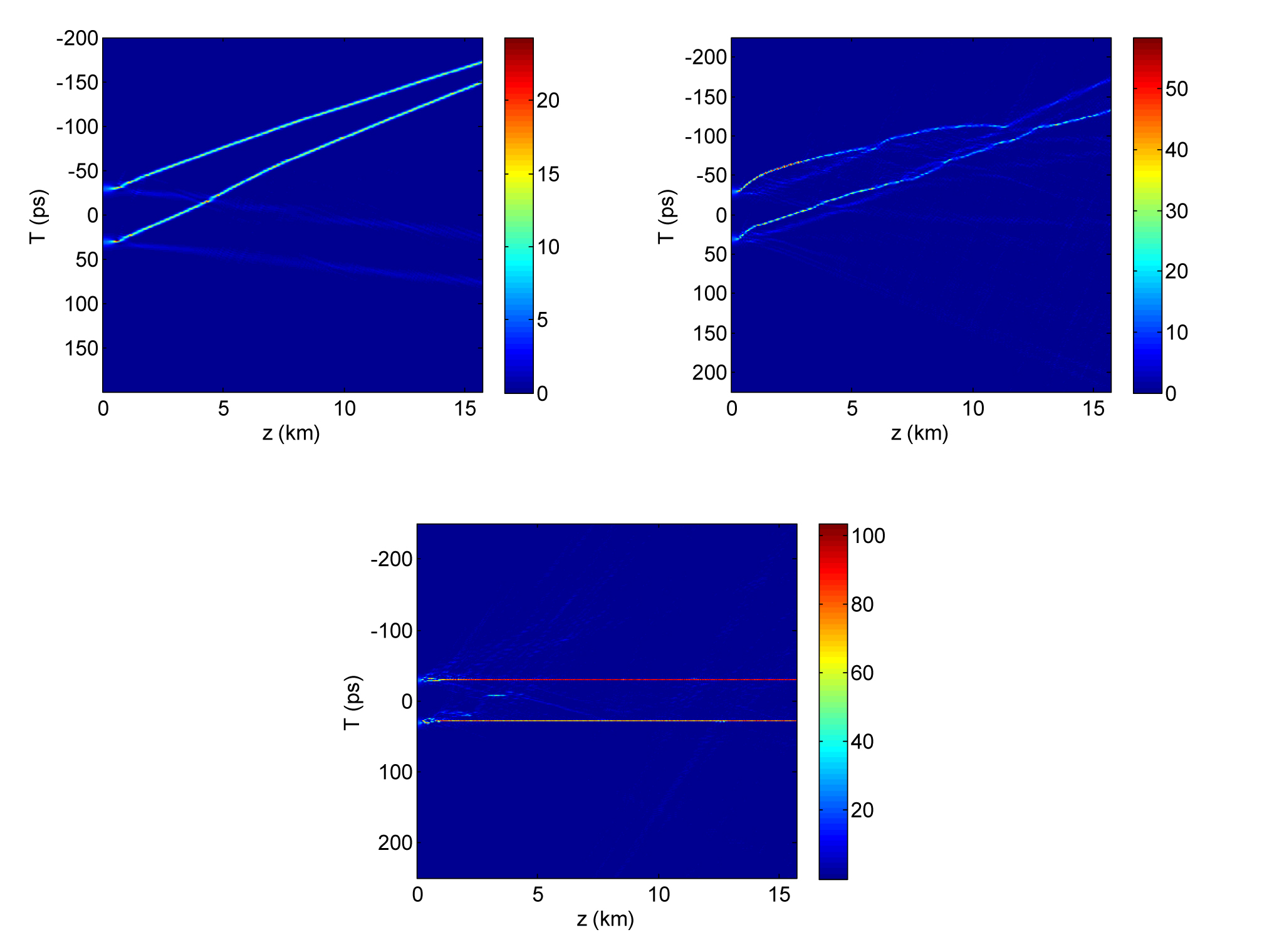
It is well known that, during higher order soliton propagation in the presence of the third order dispersion, the irregular shape of the higher order soliton disappears, and a splitting towards its fundamental constituents occurs after a considerable propagation. As for the fourth order, dispersion gives rise to two dispersive wave sidebands on the red or blue side. Our results reveal that bringing two higher order solitons together in the presence of the fourth order dispersion, a series of interactions between the components generated after their fission is obtained. In the third-order distribution, besides the fourth-order diffusion, the rare form and the supercontinuum generated by the fission of the higher-order solitons disappear, and we get two fundamental solitons propagating in parallel with a temporal shift and some inconsiderable dispersive waves. The most important aspect is that both higher-order dispersions are able to suppress the interactions of higher-order solitons thanks to the time shift induced by the third-order distribution and the intermittent compression caused by the fourth-order scattering. These results can be obtained in practice inside the dispersion-engineered photonic crystal waveguide (PhC-wg), which allows for manipulating the high order dispersion.

Author Biographies

Khadidja Khelil, Badji Mokhtar University

PhD

Department of Physics

Azzeddine Dekhane, Ecole Nationale Supérieure de Technologie et d’Ingénierie

Lecturer

LTSE Laboratory

Aissa Benselhoub, Environmental Research Center (C.R.E)

PhD, Associate Researcher

 

Stefano Bellucci, INFN Frascati National Laboratories

Senior Researcher

References

  1. Khan, K. R., Mahmood, M. F., Biswas, A. (2014). Coherent Super Continuum Generation in Photonic Crystal Fibers at Visible and Near Infrared Wavelengths. IEEE Journal of Selected Topics in Quantum Electronics, 20 (5), 573–581. doi: https://doi.org/10.1109/jstqe.2014.2302353
  2. Hernandez-Garcia, J. C., Estudillo-Ayala, J. M., Mata-Chavez, R. I., Pottiez, O., Rojas-Laguna, R., Alvarado-Mendez, E. (2013). Experimental study on a broad and flat supercontinuum spectrum generated through a system of two PCFs. Laser Physics Letters, 10 (7), 075101. doi: https://doi.org/10.1088/1612-2011/10/7/075101
  3. Dudley, J. M., Genty, G., Coen, S. (2006). Supercontinuum generation in photonic crystal fiber. Reviews of Modern Physics, 78 (4), 1135–1184. doi: https://doi.org/10.1103/revmodphys.78.1135
  4. Smirnov, S. V., Ania-Castanon, J. D., Ellingham, T. J., Kobtsev, S. M., Kukarin, S., Turitsyn, S. K. (2006). Optical spectral broadening and supercontinuum generation in telecom applications. Optical Fiber Technology, 12 (2), 122–147. doi: https://doi.org/10.1016/j.yofte.2005.07.004
  5. Lü, X., Zhu, H.-W., Meng, X.-H., Yang, Z.-C., Tian, B. (2007). Soliton solutions and a Bäcklund transformation for a generalized nonlinear Schrödinger equation with variable coefficients from optical fiber communications. Journal of Mathematical Analysis and Applications, 336 (2), 1305–1315. doi: https://doi.org/10.1016/j.jmaa.2007.03.017
  6. Meng, X.-H., Zhang, C.-Y., Li, J., Xu, T., Zhu, H.-W., Tian, B. (2007). Analytic Multi-Solitonic Solutions of Variable-Coefficient Higher-Order Nonlinear Schrödinger Models by Modified Bilinear Method with Symbolic Computation. Zeitschrift Für Naturforschung A, 62 (1-2), 13–20. doi: https://doi.org/10.1515/zna-2007-1-203
  7. Yu, T., Golovchenko, E. A., Pilipetskii, A. N., Menyuk, C. R. (1997). Dispersion-managed soliton interactions in optical fibers. Optics Letters, 22 (11), 793–795. doi: https://doi.org/10.1364/ol.22.000793
  8. Herrmann, J., Griebner, U., Zhavoronkov, N., Husakou, A., Nickel, D., Knight, J. C. et al. (2002). Experimental Evidence for Supercontinuum Generation by Fission of Higher-Order Solitons in Photonic Fibers. Physical Review Letters, 88 (17). doi: https://doi.org/10.1103/physrevlett.88.173901
  9. Wai, P. K. A., Chen, H. H., Lee, Y. C. (1990). Radiations by «solitons» at the zero group-dispersion wavelength of single-mode optical fibers. Physical Review A, 41 (1), 426–439. doi: https://doi.org/10.1103/physreva.41.426
  10. Elgin, J. N. (1993). Perturbations of optical solitons. Physical Review A, 47 (5), 4331–4341. doi: https://doi.org/10.1103/physreva.47.4331
  11. Karpman, V. I. (1993). Radiation by solitons due to higher-order dispersion. Physical Review E, 47 (3), 2073–2082. doi: https://doi.org/10.1103/physreve.47.2073
  12. Akhmediev, N., Karlsson, M. (1995). Cherenkov radiation emitted by solitons in optical fibers. Physical Review A, 51 (3), 2602–2607. doi: https://doi.org/10.1103/physreva.51.2602
  13. Roy, S., Bhadra, S. K., Agrawal, G. P. (2009). Dispersive waves emitted by solitons perturbed by third-order dispersion inside optical fibers. Physical Review A, 79 (2). doi: https://doi.org/10.1103/physreva.79.023824
  14. Wai, P. K. A., Menyuk, C. R., Lee, Y. C., Chen, H. H. (1986). Nonlinear pulse propagation in the neighborhood of the zero-dispersion wavelength of monomode optical fibers. Optics Letters, 11 (7), 464. doi: https://doi.org/10.1364/ol.11.000464
  15. Biswas, A. (2004). Stochastic perturbation of optical solitons in Schrödinger–Hirota equation. Optics Communications, 239 (4-6), 461–466. doi: https://doi.org/10.1016/j.optcom.2004.06.047
  16. Biswas, A., Jawad, A. J. M., Manrakhan, W. N., Sarma, A. K., Khan, K. R. (2012). Optical solitons and complexitons of the Schrödinger–Hirota equation. Optics & Laser Technology, 44 (7), 2265–2269. doi: https://doi.org/10.1016/j.optlastec.2012.02.028
  17. Kohl, R., Milovic, D., Zerrad, E., Biswas, A. (2009). Soliton perturbation theory for dispersion-managed optical fibers. Journal of Nonlinear Optical Physics & Materials, 18 (2), 227–270. doi: https://doi.org/10.1142/s0218863509004592
  18. Topkara, E., Milovic, D., Sarma, A. K., Zerrad, E., Biswas, A. (2010). Optical soliton perturbation with full nonlinearity in non-Kerr law media. Journal of Optical and Fiber Communications Research, 7 (1-4), 43–59. doi: https://doi.org/10.1007/s10297-010-9007-3
  19. Biswas, A., Topkara, E., Johnson, S., Zerrad, E., Konar, S. (2011). Quasi-stationary optical solitons in non-kerr law media with full nonlinearity. Journal of nonlinear optical physics & materials, 20 (3), 309–325. doi: https://doi.org/10.1142/s0218863511006108
  20. Biswas, A., Milovic, D., Savescu, M., Mahmood, M. F., Khan, K. R., Kohl, R. (2012). Optical soliton perturbation in nanofibers with improved nonlinear Schrodinger’s equation by semi-inverse variational principle. Journal of Nonlinear Optical Physics & Materials, 12 (4). doi: https://doi.org/10.1142/s0218863512500543
  21. Biswas, A., Milovic, D., Girgis, L. (2013). Quasi-stationary optical Gaussons. Optik – International Journal for Light and Electron Optics, 124 (17), 2959–2962. doi: https://doi.org/10.1016/j.ijleo.2012.09.055
  22. Xu, Y., Jovanoski, Z., Bouasla, A., Triki, H., Moraru, L., Biswas, A. (2013). Optical solitons in multi-dimensions with spatio-temporal dispersion and non-kerr law nonlinearity. Journal of Nonlinear Optical Physics & Materials, 22 (3), 1350035. doi: https://doi.org/10.1142/s0218863513500355
  23. Biswas, A., Khan, K., Rahman, A., Yildirim, A., Hayat, T., Aldossary, O. M. (2012). Bright and dark optical solitons in birefringent fibers with Hamiltonian perturbations and Kerr law nonlinearity. The Journal of Optoelectronics and Advanced Materials, 14 (7-8), 571–576.
  24. Bhrawy, A. H., Alshaery, A. A., Hilal, E. M., Manrakhan, W. N., Savescu, M., Biswas, A. (2014). Dispersive optical solitons with Schrödinger–Hirota equation. Journal of Nonlinear Optical Physics & Materials, 23 (1), 1450014. doi: https://doi.org/10.1142/s0218863514500143
  25. Wang, J., Wang, S., Chu, X., Sun, M. (2013). Numerical Study on Optical Solitons Transmission System with 40 Gbit/s in the Photonic Crystal Fiber. Optics and Photonics Journal, 3 (2), 141–146. doi: https://doi.org/10.4236/opj.2013.32023
  26. Elgin, J. N., Brabec, T., Kelly, S. M. J. (1995). A perturbative theory of soliton propagation in the presence of third order dispersion. Optics Communications, 114 (3-4), 321–328. doi: https://doi.org/10.1016/0030-4018(94)00602-q
  27. Biswas, A., Milovic, D. (2009). Optical Solitons with Fourth Order Dispersion and Dual-power Law Nonlinearity. International Journal of Nonlinear Science, 7 (4), 443–447.
  28. Elshater, M. E. M., Zayed, E. M. E., Al-Nowehy, A-G. (2016). Solitons and other solutions to nonlinear Schrödinger equation with fourth-order dispersion and dual power law nonlinearity using several different techniques. Optik, International Journal for Light and Electron Optics.
  29. Khelil, K., Saouchi, K., Bahloul, D. (2020). Effect of fourth order dispersion on solitonic interactions. Ukranian Journal of Physics, 4.
Higher order dispersions effect on high-order soliton interactions

Downloads

Published

2023-04-28

How to Cite

Khelil, K., Dekhane, A., Benselhoub, A., & Bellucci, S. (2023). Higher order dispersions effect on high-order soliton interactions. Technology Audit and Production Reserves, 2(1(70), 24–29. https://doi.org/10.15587/2706-5448.2023.277346

Issue

Vol. 2 No. 1(70) (2023): Industrial and technology systems

Section

Electrical Engineering and Industrial Electronics

License

Copyright (c) 2023 Khadidja Khelil, Azzeddine Dekhane, Aissa Benselhoub, Stefano Bellucci

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.