Вплив дисперсій вищого порядку на взаємодії солітонів високого порядку
DOI:
https://doi.org/10.15587/2706-5448.2023.277346Ключові слова:
солітони вищих порядків, поділ солітонів, дисперсії, нелінійність, оптичне волокно, суперконтинуумАнотація
Об’єктом дослідження є усунення взаємодії солітонів вищого порядку шляхом введення дисперсій третього та четвертого порядків всередину оптичного волокна. Результати отримані шляхом моделювання нелінійного рівняння Шредінгера, яке моделює поширення солітонів в оптичному волокні за допомогою методу швидкого перетворення Фур’є.
Взаємодія двох солітонів вищого порядку за рахунок притягання їх електричного поля може призвести до втрати властивостей солітонів. Отже, це може запобігти використанню солітонів у високошвидкісних волоконно-оптичних системах зв’язку, оскільки це збільшує частоту бітових помилок, значно обмежуючи потенціал системи зв’язку. Щоб вирішити цю проблему, необхідно зменшити помилку швидкості потоку, уникаючи взаємодії співпоширених солітонів, коли вони знаходяться занадто близько.
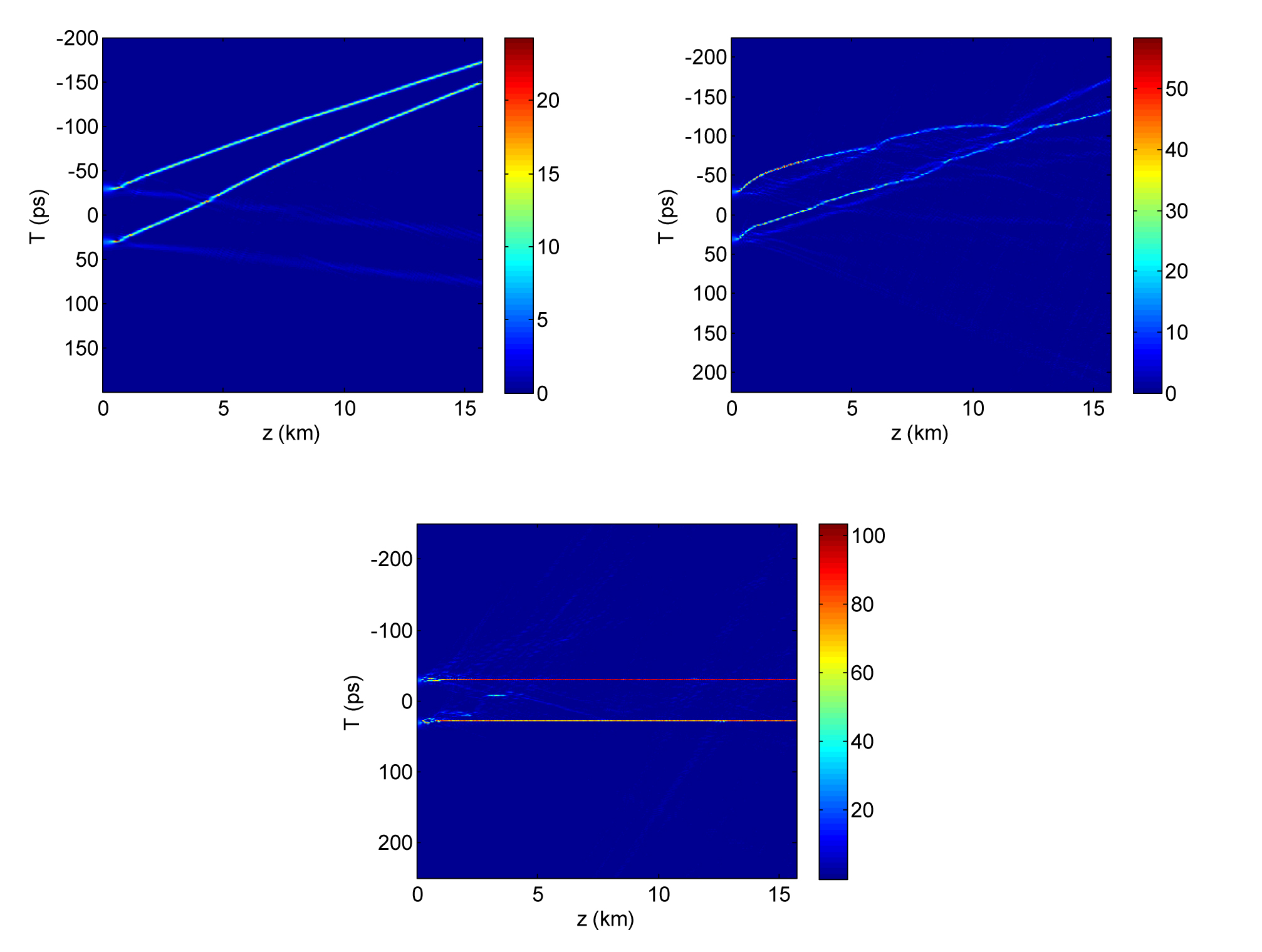
Добре відомо, що під час розповсюдження солітону вищого порядку за наявності дисперсії третього порядку неправильна форма солітону вищого порядку зникає, і після значного розповсюдження відбувається розщеплення до його основних складових. Що стосується четвертого порядку, дисперсія породжує дві бічні смуги дисперсійної хвилі на червоній або синій стороні. Приведені результати показують, що об’єднання двох солітонів вищого порядку за наявності дисперсії четвертого порядку забезпечує серію взаємодій між компонентами, що виникають після їхнього поділу. У розподілі третього порядку, окрім дифузії четвертого порядку, зникає рідкісна форма та суперконтинуум, створений поділом солітонів вищого порядку, і ми отримуємо два фундаментальних солітони, що поширюються паралельно з часовим зсувом і деякими незначними дисперсійними хвилями. Найважливішим аспектом є те, що обидві дисперсії вищого порядку здатні пригнічувати взаємодію солітонів вищого порядку завдяки часовому зсуву, викликаному розподілом третього порядку, і періодичному стисненню, спричиненому розсіюванням четвертого порядку. Ці результати можна отримати на практиці всередині фотонно-кристалічного хвилеводу (PhC-wg), створеного за допомогою дисперсії, що дозволяє маніпулювати дисперсією високого порядку.
Посилання
- Khan, K. R., Mahmood, M. F., Biswas, A. (2014). Coherent Super Continuum Generation in Photonic Crystal Fibers at Visible and Near Infrared Wavelengths. IEEE Journal of Selected Topics in Quantum Electronics, 20 (5), 573–581. doi: https://doi.org/10.1109/jstqe.2014.2302353
- Hernandez-Garcia, J. C., Estudillo-Ayala, J. M., Mata-Chavez, R. I., Pottiez, O., Rojas-Laguna, R., Alvarado-Mendez, E. (2013). Experimental study on a broad and flat supercontinuum spectrum generated through a system of two PCFs. Laser Physics Letters, 10 (7), 075101. doi: https://doi.org/10.1088/1612-2011/10/7/075101
- Dudley, J. M., Genty, G., Coen, S. (2006). Supercontinuum generation in photonic crystal fiber. Reviews of Modern Physics, 78 (4), 1135–1184. doi: https://doi.org/10.1103/revmodphys.78.1135
- Smirnov, S. V., Ania-Castanon, J. D., Ellingham, T. J., Kobtsev, S. M., Kukarin, S., Turitsyn, S. K. (2006). Optical spectral broadening and supercontinuum generation in telecom applications. Optical Fiber Technology, 12 (2), 122–147. doi: https://doi.org/10.1016/j.yofte.2005.07.004
- Lü, X., Zhu, H.-W., Meng, X.-H., Yang, Z.-C., Tian, B. (2007). Soliton solutions and a Bäcklund transformation for a generalized nonlinear Schrödinger equation with variable coefficients from optical fiber communications. Journal of Mathematical Analysis and Applications, 336 (2), 1305–1315. doi: https://doi.org/10.1016/j.jmaa.2007.03.017
- Meng, X.-H., Zhang, C.-Y., Li, J., Xu, T., Zhu, H.-W., Tian, B. (2007). Analytic Multi-Solitonic Solutions of Variable-Coefficient Higher-Order Nonlinear Schrödinger Models by Modified Bilinear Method with Symbolic Computation. Zeitschrift Für Naturforschung A, 62 (1-2), 13–20. doi: https://doi.org/10.1515/zna-2007-1-203
- Yu, T., Golovchenko, E. A., Pilipetskii, A. N., Menyuk, C. R. (1997). Dispersion-managed soliton interactions in optical fibers. Optics Letters, 22 (11), 793–795. doi: https://doi.org/10.1364/ol.22.000793
- Herrmann, J., Griebner, U., Zhavoronkov, N., Husakou, A., Nickel, D., Knight, J. C. et al. (2002). Experimental Evidence for Supercontinuum Generation by Fission of Higher-Order Solitons in Photonic Fibers. Physical Review Letters, 88 (17). doi: https://doi.org/10.1103/physrevlett.88.173901
- Wai, P. K. A., Chen, H. H., Lee, Y. C. (1990). Radiations by «solitons» at the zero group-dispersion wavelength of single-mode optical fibers. Physical Review A, 41 (1), 426–439. doi: https://doi.org/10.1103/physreva.41.426
- Elgin, J. N. (1993). Perturbations of optical solitons. Physical Review A, 47 (5), 4331–4341. doi: https://doi.org/10.1103/physreva.47.4331
- Karpman, V. I. (1993). Radiation by solitons due to higher-order dispersion. Physical Review E, 47 (3), 2073–2082. doi: https://doi.org/10.1103/physreve.47.2073
- Akhmediev, N., Karlsson, M. (1995). Cherenkov radiation emitted by solitons in optical fibers. Physical Review A, 51 (3), 2602–2607. doi: https://doi.org/10.1103/physreva.51.2602
- Roy, S., Bhadra, S. K., Agrawal, G. P. (2009). Dispersive waves emitted by solitons perturbed by third-order dispersion inside optical fibers. Physical Review A, 79 (2). doi: https://doi.org/10.1103/physreva.79.023824
- Wai, P. K. A., Menyuk, C. R., Lee, Y. C., Chen, H. H. (1986). Nonlinear pulse propagation in the neighborhood of the zero-dispersion wavelength of monomode optical fibers. Optics Letters, 11 (7), 464. doi: https://doi.org/10.1364/ol.11.000464
- Biswas, A. (2004). Stochastic perturbation of optical solitons in Schrödinger–Hirota equation. Optics Communications, 239 (4-6), 461–466. doi: https://doi.org/10.1016/j.optcom.2004.06.047
- Biswas, A., Jawad, A. J. M., Manrakhan, W. N., Sarma, A. K., Khan, K. R. (2012). Optical solitons and complexitons of the Schrödinger–Hirota equation. Optics & Laser Technology, 44 (7), 2265–2269. doi: https://doi.org/10.1016/j.optlastec.2012.02.028
- Kohl, R., Milovic, D., Zerrad, E., Biswas, A. (2009). Soliton perturbation theory for dispersion-managed optical fibers. Journal of Nonlinear Optical Physics & Materials, 18 (2), 227–270. doi: https://doi.org/10.1142/s0218863509004592
- Topkara, E., Milovic, D., Sarma, A. K., Zerrad, E., Biswas, A. (2010). Optical soliton perturbation with full nonlinearity in non-Kerr law media. Journal of Optical and Fiber Communications Research, 7 (1-4), 43–59. doi: https://doi.org/10.1007/s10297-010-9007-3
- Biswas, A., Topkara, E., Johnson, S., Zerrad, E., Konar, S. (2011). Quasi-stationary optical solitons in non-kerr law media with full nonlinearity. Journal of nonlinear optical physics & materials, 20 (3), 309–325. doi: https://doi.org/10.1142/s0218863511006108
- Biswas, A., Milovic, D., Savescu, M., Mahmood, M. F., Khan, K. R., Kohl, R. (2012). Optical soliton perturbation in nanofibers with improved nonlinear Schrodinger’s equation by semi-inverse variational principle. Journal of Nonlinear Optical Physics & Materials, 12 (4). doi: https://doi.org/10.1142/s0218863512500543
- Biswas, A., Milovic, D., Girgis, L. (2013). Quasi-stationary optical Gaussons. Optik – International Journal for Light and Electron Optics, 124 (17), 2959–2962. doi: https://doi.org/10.1016/j.ijleo.2012.09.055
- Xu, Y., Jovanoski, Z., Bouasla, A., Triki, H., Moraru, L., Biswas, A. (2013). Optical solitons in multi-dimensions with spatio-temporal dispersion and non-kerr law nonlinearity. Journal of Nonlinear Optical Physics & Materials, 22 (3), 1350035. doi: https://doi.org/10.1142/s0218863513500355
- Biswas, A., Khan, K., Rahman, A., Yildirim, A., Hayat, T., Aldossary, O. M. (2012). Bright and dark optical solitons in birefringent fibers with Hamiltonian perturbations and Kerr law nonlinearity. The Journal of Optoelectronics and Advanced Materials, 14 (7-8), 571–576.
- Bhrawy, A. H., Alshaery, A. A., Hilal, E. M., Manrakhan, W. N., Savescu, M., Biswas, A. (2014). Dispersive optical solitons with Schrödinger–Hirota equation. Journal of Nonlinear Optical Physics & Materials, 23 (1), 1450014. doi: https://doi.org/10.1142/s0218863514500143
- Wang, J., Wang, S., Chu, X., Sun, M. (2013). Numerical Study on Optical Solitons Transmission System with 40 Gbit/s in the Photonic Crystal Fiber. Optics and Photonics Journal, 3 (2), 141–146. doi: https://doi.org/10.4236/opj.2013.32023
- Elgin, J. N., Brabec, T., Kelly, S. M. J. (1995). A perturbative theory of soliton propagation in the presence of third order dispersion. Optics Communications, 114 (3-4), 321–328. doi: https://doi.org/10.1016/0030-4018(94)00602-q
- Biswas, A., Milovic, D. (2009). Optical Solitons with Fourth Order Dispersion and Dual-power Law Nonlinearity. International Journal of Nonlinear Science, 7 (4), 443–447.
- Elshater, M. E. M., Zayed, E. M. E., Al-Nowehy, A-G. (2016). Solitons and other solutions to nonlinear Schrödinger equation with fourth-order dispersion and dual power law nonlinearity using several different techniques. Optik, International Journal for Light and Electron Optics.
- Khelil, K., Saouchi, K., Bahloul, D. (2020). Effect of fourth order dispersion on solitonic interactions. Ukranian Journal of Physics, 4.
##submission.downloads##
Опубліковано
Як цитувати
Номер
Розділ
Ліцензія
Авторське право (c) 2023 Khadidja Khelil, Azzeddine Dekhane, Aissa Benselhoub, Stefano Bellucci

Ця робота ліцензується відповідно до Creative Commons Attribution 4.0 International License.
Закріплення та умови передачі авторських прав (ідентифікація авторства) здійснюється у Ліцензійному договорі. Зокрема, автори залишають за собою право на авторство свого рукопису та передають журналу право першої публікації цієї роботи на умовах ліцензії Creative Commons CC BY. При цьому вони мають право укладати самостійно додаткові угоди, що стосуються неексклюзивного поширення роботи у тому вигляді, в якому вона була опублікована цим журналом, але за умови збереження посилання на першу публікацію статті в цьому журналі.








