Development of floating point operating devices

Authors

DOI:

https://doi.org/10.15587/2706-5448.2023.290127

Keywords:

floating-point multiplier, superscalar processor, associativity law, Baugh-Wooley algorithm, CISC-RISC

Abstract

The paper shows a well-known approach to the construction of cores in multi-core microprocessors, which is based on the application of a data flow graph-driven calculation model. The architecture of such kernels is based on the application of the reduced instruction set level data flow model proposed by Yale Patt. The object of research is a model of calculations based on data flow management in a multi-core microprocessor.

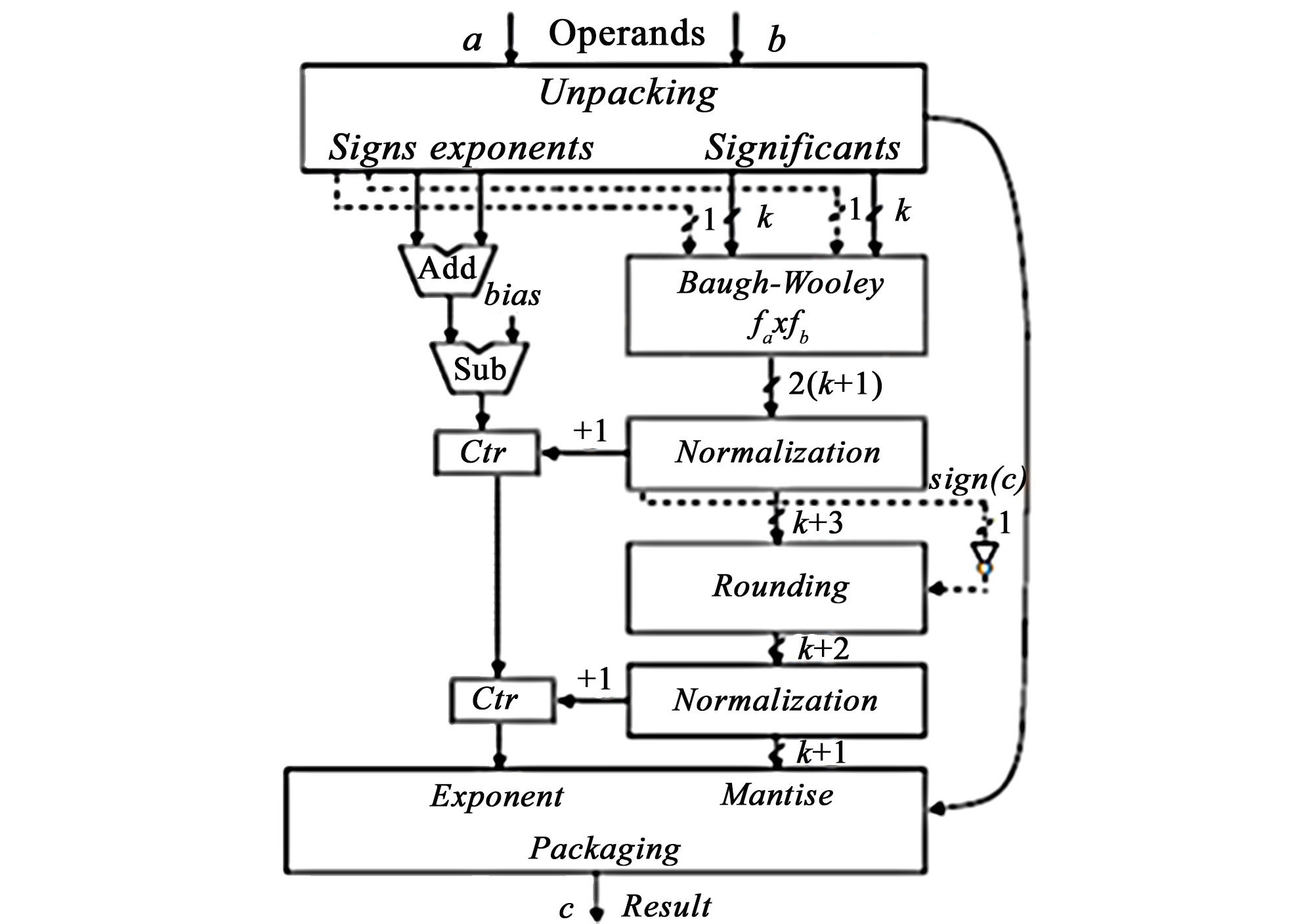
The results of the floating-point multiplier development that can be dynamically reconfigured to handle five different formats of floating-point operands and an approach to the construction of an operating device for addition-subtraction of a sequence of floating-point numbers are presented, for which the law of associativity is fulfilled without additional programming complications. On the basis of the developed circuit of the floating-point multiplier, it is possible to implement various variants of the high-speed multiplier with both fixed and floating points, which may find commercial application. By adding memory elements to each of the multiplier segments, it is possible to get options for building very fast pipeline multipliers. The multiplier scheme has a limitation: the exponent is not evaluated for denormalized operands, but the standard for floating-point arithmetic does not require that denormalized operands be handled. In such cases, the multiplier packs infinity as the result.

The implementation of an inter-core operating device of a floating-point adder-subtractor can be considered as a new approach to the practical solution of dynamic planning tasks when performing addition-subtraction operations within the framework of a multi-core microprocessor. The limitations of its implementation are related to the large amount of hardware costs required for implementation. To assess this complexity, an assessment of the value of the bits of its main blocks for various formats of representing floating-point numbers, in accordance with the floating-point standard, was carried out.

Author Biographies

Georgi Luсkij, National Technical University of Ukraine «Igor Sikorsky Kyiv Polytechnic Institute»

Doctor of Technical Science, Professor

Department of Computer Engineering

Oleksandr Dolholenko, National Technical University of Ukraine «Igor Sikorsky Kyiv Polytechnic Institute»

PhD, Associate Professor, Senior Researcher

Department of Informatics

References

  1. Patt, Y., Hwu, W. et al. (1986). Experiments with HPS, a Restricted Data Flow Micro architecture for High Performance Computers. COMPCON 86, 254–258.
  2. Simone, M., Essen, A., Ike, A., Krishnamoorthy, A., Maruyama, T., Patkar, N. et al. (1995). Implementation trade-offs in using a restricted data flow architecture in a high performance RISC microprocessor. ACM SIGARCH Computer Architecture News, 23 (2), 151–162. doi: https://doi.org/10.1145/225830.224411
  3. Hennessy, J. L., Patterson, D. A. (2019). Computer Architecture: A Cuantitative Approach. Morgan Kaufmann, 1527.
  4. Kanter, D. (2012). Intel’s Haswell CPU Microarchitecture. Available at: http://www.realworldtech.com/haswell-cpu/
  5. Shen, J., Lipasti, M. (2013). Modern Processor Design: Fundamentals of Superscalar Processors. Waveland Press, 642.
  6. Lutskyi, H. M., Dolholenko, O. M., Aksonenko, S. V., Storozhuk, V. O. (2014). Modeliuvannia obmezhenoi realizatsii arkhitektury potoku danykh v strukturi superskaliarnoho protsesora. Visnyk NTUU «KPI». Informatyka, upravlinnia ta obchysliuvalna tekhnika, 60, 83–94.
  7. Dolholenko, A. O., Yatsun, V. O. (2016). Realizatsiia operatsiinoho prystroiu sumatora/vidnimacha z plavaiuchoiu krapkoiu dlia yadra superskaliarnoho protsesora. Visnyk NTUU «KPI». Informatyka, upravlinnia ta obchysliuvalna tekhnika, 64, 106–116.
  8. IEEE 754: Standard for Binary Floating-Point Arithmetic (2019). Available at: https://grouper.ieee.org/groups/msc/ANSI_IEEE-Std-754-2019/background/
  9. What Every Computer Scientist Should Know About Floating-Point Arithmetic. Available at: https://ece.uwaterloo.ca/~dwharder/NumericalAnalysis/02Numerics/Double/paper.pdf
  10. Knut, D. (1977). Iskusstvo programmirovaniia dlia EVM. Vol. 2. Moscow: Mir, 724.
  11. Mak-Kraken, D., Dorn, U. (1977). Chislennye metody i programmirovanie na FORTRANE. Moscow: Mir, 584.
  12. Strictly, there exist other variants of compensated summation as well: see Higham, Nicholas (2002). Accuracy and Stability of Numerical Algorithms. SIAM, 110–123.
  13. Lutskyi, H. M. et al. (2016). Metody ta zasoby pidvyshchennia efektyvnosti rishennia zdach na osnovi perestroiuvanykh obchysliuvalnykh zasobiv na PLIS – Zakl. zvit po NDR No. DR 0216U007635. Kyiv, 244.
  14. Baugh, C. R., Wooley, B. A. (1973). A Two’s Complement Parallel Array Multiplication Algorithm. IEEE Transactions on Computers, C–22 (12), 1045–1047. doi: https://doi.org/10.1109/t-c.1973.223648
  15. Parhami, B. (2000). Computer Arithmetic. Algorithms and Hardware Designs. New York: Oxford University Press, 491.
Development of floating point operating devices

Downloads

Published

2023-10-31

How to Cite

Luсkij G., & Dolholenko, O. (2023). Development of floating point operating devices. Technology Audit and Production Reserves, 5(2(73), 11–17. https://doi.org/10.15587/2706-5448.2023.290127

Issue

Vol. 5 No. 2(73) (2023): Information and control systems

Section

Information Technologies

License

Copyright (c) 2023 Georgi Luсkij, Oleksandr Dolholenko

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.