The graph theoretic formulation of the team formation problem based on the factor of competition
DOI:
https://doi.org/10.15587/2706-5448.2024.310570Keywords:
teamwork, pareto set, multi-criteria objective functions, graph, multi-criteria optimization, competitionAbstract
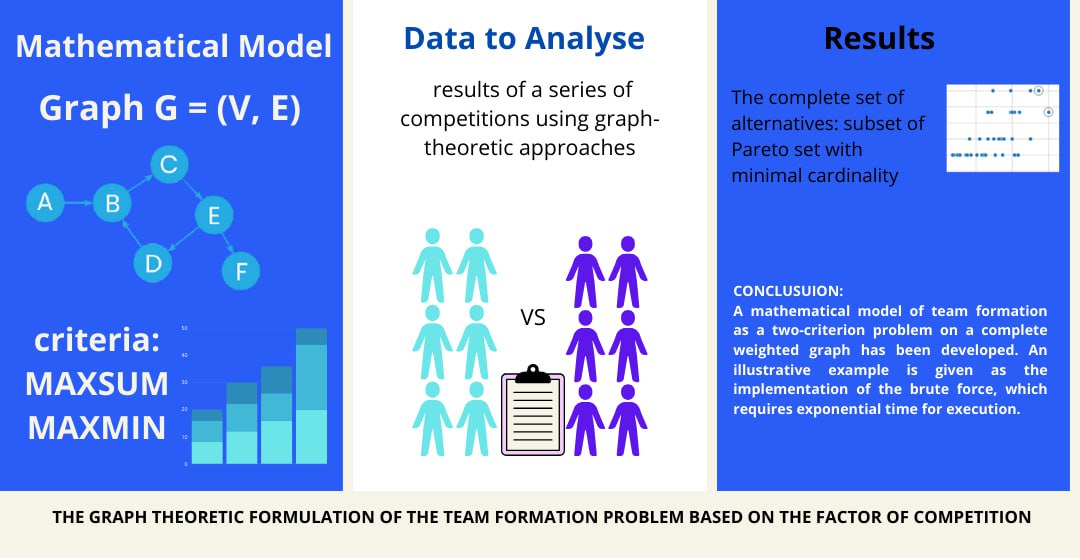
The object of the research is to increase the level of productivity of teamwork due to the effective selection of participants who demonstrate the highest level of productivity in cooperation. The presented research is aimed at the mathematical formalization of the problem of team formation based on the results of a series of competitions using graph-theoretic approaches. Each competition in this series involves teams with the same number of participants. The composition of the team necessarily changes for each subsequent competition. After the competitive series, the obtained information about the teams' composition and their results is evaluated for the success of the interaction of the participants, which can be used in the formation of successful teams. A graph-theoretic formalization of the team formation problem on a complete undirected weighted graph has been developed. The set of vertices of this graph corresponds to the set of potential participants. Each edge is weighted with a number that reflects the quality of the interaction between the two participants. A valid solution is to cover the graph with cliques, the size of which is determined by the number of team members. A mathematical model of a two-criterion problem with MAXSUM and MAXMIN criteria was built, where the first criterion evaluates the overall success of the created teams, the second criterion evaluates the «weakest link», allowing to choose the option that maximizes the minimum edge weights for each clique. A two-criterion objective function defines a Pareto set consisting of all Pareto optima in the set of admissible solutions. The algorithmic problem of finding the complete set of alternatives, which is a subset of the Pareto set of minimum power when the condition of equality of the objective functions for the complete set of alternatives and the Pareto set is fulfilled, is considered. The weight of the edges of the graph is calculated using the scores obtained during the series of competitions. In practice, the research results can be used as a basis for the development of team building techniques.
References
- Kozlowski, S. W. J., Ilgen, D. R. (2006). Enhancing the Effectiveness of Work Groups and Teams. Psychological Science in the Public Interest, 7 (3), 77–124. https://doi.org/10.1111/j.1529-1006.2006.00030.x
- Acosta Mejía, C., Cambra Carrizo, G. I., Martinez-Carrasco, J., Cerda, M., Kang, M., Villalba, H., Yépez, C. (2024). Unveiling the IDB’s Project Executing Units: Performance Indicators, Results-Based Management, and Demand for Knowledge. Inter-American Development Bank. https://doi.org/10.18235/0013040
- Sa’diyah, K. (2024). Occupational Health and Safety, Training, and Teamwork for Hospital Medical Performance. Safety and Health for Medical Workers, 1 (1), 29–38. https://doi.org/10.69725/ehxp3d73
- Poth, A., Kottke, M., Riel, A.; Yilmaz, M., Clarke, P., Messnarz, R., Reiner, M. (Eds.) (2021). Orchestrating Agile IT Quality Management for Complex Solution Development Through Topic-Specific Partnerships in Large Enterprises – An Example on the EFIS Framework. Systems, Software and Services Process Improvement. EuroSPI 2021. Communications in Computer and Information Science. Vol. 1442. Cham: Springer, 88–104. https://doi.org/10.1007/978-3-030-85521-5_7
- Pasupa, T., Suzuki, S. (2022). Two-Stage Adaptive Large Neighbourhood Search for Team Formation and Worker Assignment Problems in Cellular Manufacturing Systems. Applied Sciences, 12 (16), 8323. https://doi.org/10.3390/app12168323
- Yang, W. Z. (2024). Teamwork triumphs: fostering student development through cooperative learning in university physical education. International Journal of Current Educational Practice, 12 (2), 114–120. https://doi.org/10.5281/zenodo.10954880
- Hebles, M., Jara, M., Alvarez de E, C. Y. (2020). Teamwork competence and collaborative learning in entrepreneurship training. European J. of International Management, 20 (2), 238–255. https://doi.org/10.1504/ejim.2020.10022225
- Sangadji, H. (2023). The Influence of Emotional Intelligence, Teamwork, And Organizational Citizenship Behavior on Performance Agricultural Extension Workers in Banten Province. IJHCM (International Journal of Human Capital Management), 7 (1), 141–157. https://doi.org/10.21009/ijhcm.07.01.11
- Feitosa, J., Grossman, R., Kramer, W. S., Salas, E. (2020). Measuring team trust: A critical and meta‐analytical review. Journal of Organizational Behavior, 41 (5), 479–501. https://doi.org/10.1002/job.2436
- Delfgaauw, J., Dur, R., Onemu, O., Sol, J. (2022). Team Incentives, Social Cohesion, and Performance: A Natural Field Experiment. Management Science, 68 (1), 230–256. https://doi.org/10.1287/mnsc.2020.3901
- Makanda, I. L. D., Jiang, P., Yang, M., Shi, H. (2023). Emergence of collective intelligence in industrial cyber-physical-social systems for collaborative task allocation and defect detection. Computers in Industry, 152, 104006. https://doi.org/10.1016/j.compind.2023.104006
- Ai, W., Chen, Y., Mei, Q., Ye, J., Zhang, L. (2023). Putting Teams into the Gig Economy: A Field Experiment at a Ride-Sharing Platform. Management Science, 69 (9), 5336–5353. https://doi.org/10.1287/mnsc.2022.4624
- Ertac, S., Gümren, M., Koçkesen, L. (2019). Strategic feedback in teams: Theory and experimental evidence. Journal of Economic Behavior & Organization, 162, 1–23. https://doi.org/10.1016/j.jebo.2019.04.005
- Fischer, M., Rilke, R. M., Yurtoglu, B. B. (2023). When, and why, do teams benefit from self-selection? Experimental Economics, 26 (4), 749–774. https://doi.org/10.1007/s10683-023-09800-2
- Zhao, M., Eadeh, F. R., Nguyen, T.-N., Gupta, P., Admoni, H., Gonzalez, C., Woolley, A. W. (2023). Teaching agents to understand teamwork: Evaluating and predicting collective intelligence as a latent variable via Hidden Markov Models. Computers in Human Behavior, 139, 107524. https://doi.org/10.1016/j.chb.2022.107524
- Mansour, T. (2012). Combinatorics of Set Partitions. Chapman and Hall/CRC. https://doi.org/10.1201/b12691
- Perepelitsa, V. A., Tereschenko, E. V. (2018). On Complete and Quasi-Complete Two-Criteria Optimization Problems on Graphs. Cybernetics and Systems Analysis, 54 (3), 385–390. https://doi.org/10.1007/s10559-018-0040-1
- Ohirko, O. I., Halayko, N. V. (2017). Teoriya ymovirnostey ta matematychna statystyka. Lviv: LʹvDUVS, 292.
Downloads
Published
How to Cite
Issue
Section
License
Copyright (c) 2024 Anton Riabenko, Elina Tereschenko, Anna Bakurova, Andrii Pyrozhok, Olexiy Kuzkin

This work is licensed under a Creative Commons Attribution 4.0 International License.
The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.







