Exploration of describing the vector-parametric bi-spline, defined by the forth degree spline with control points incident with surface of appropriate smoothness

Abstract

The article proposes description technique for spline vector & parametrical surfaces of the fourth degree with control points incidental to the surface and gives  testing examples of application of this technique. Main purpose of researches is to develop an algorithm for solving some application problems which often impose specific demands to tools available with developers’ or designers’ workplace. For instance, it sometime becomes troublesome to produce smooth configuration, since the obtained curve does not belong to pre-set dotted carcass.

The technique of producing a vector & parametrical bispline with control points incidental (belonging) to relevant surface is proposed to overcome such inconvenience. Hence, a polynomial function of the fourth degree determined with five points x_0, y_0, x_1, y_1, x_2, y_2, x_3, y_3, x_4, y₄  may be represented, as below:

 

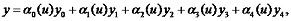
with function α_i(u) being the Lagrange polynomial coefficients.

Polynomial equation in matrix format may be expressed, as follows:

 

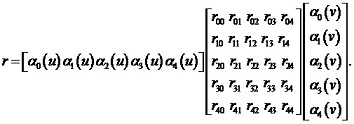
With provided derivatives equity up to the third degree (inclusive) the equity of compound derivatives along the gluing line criterion is also met (i. e. continuity of the second quadric form is achieved throughout the entire surface). Equity of the compound derivatives should be achieved to obtain fine smoothness of the third degree surface, i. e.:

 

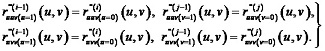
Calculation formulae for spline with third degree of smoothness should be applied to achieve this effect. Thus linear equations system with quadrodiagonal leading matrix may be obtained by means of preset three boundary conditions (thus increasing the flexibility of the method) providing a stable and unambiguous solution. Algorithm for development of the fourth degree bispline with control points belonging to relevant surface is developed. Results of the research may be helpful for developers, designers, APS users providing them with additional opportunities in developing smooth curved contours for elements and parts of machinery operating in mobile environments.

Test examples are provided for the fourth degree bisplines with third degree smoothness with control points incidental to the surface.

The proposed algorithm is suggested for implementation to improve efficient work of constructors, designers, developers.