Research of algorithm for calculating the vector-parametric bispline based on polynomial of the fourth degree

Authors

  • Александр Михайлович Ковтун Danube Institute of National University «Odessa Maritime Academy», 9, Fanagoriyskaja Str., Izmail, Odessa Region, 68600-Ukraine, Ukraine https://orcid.org/0000-0002-6531-2561

DOI:

https://doi.org/10.15587/2312-8372.2016.80457

Keywords:

segment of three points and two first derivatives, vector-parametric spline of fourth degree

Abstract

In the course of the audit process of the vector-parametric spline of fourth degree on the basis of a segment of three points and two first derivatives at the end points is easy to see that it cannot be set to the same number of boundary conditions at both ends, as for polynomials of third and fifth degree, because a polynomial of the fourth degree is «unbalanced».

New method is proposed to eliminate these disadvantages in the design of fourth degree splines and bisplines (vector parametric surfaces) based on them.

It is proposed to consider the next variant of polynomial of the fourth degree for bispline design: the endpoints, derivatives in them and another middle point are given.

Based on the proposed functions of the polynomial:

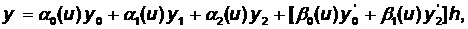
Vector parametric spline of fourth degree on the basis of a segment of three points and two first derivatives is noted:

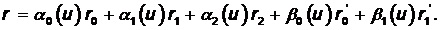
Based on the segment of the fourth degree for the portions of the surface recorded this equation is noted:

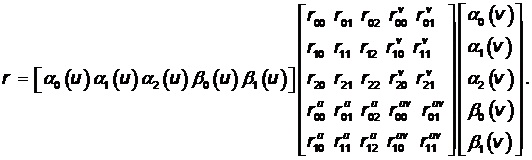
 To specify a portion it must have not only first derivatives but also the mixed derivatives at the nodal points.

Based on these formulas, it became possible to write a test program for visualization of bispline (vector parametric surface) fourth degree in the language Auto Lisp in AutoCAD, spline of fourth degree showed good «custom» properties, the surface is adequate to the input data, subjectively nice-looking.

The paper shows the ability of the splines of the fourth degree to give biplane. Due to the peculiarities of their structure (the ability to give an additional medial condition) the proposed curve has an additional possibility of a more correct and adequate to the task of specifying the conditions. The achieved effect (a new polynomial) gives a method the right to life for designing smooth curves and surfaces.

Author Biography

Александр Михайлович Ковтун, Danube Institute of National University «Odessa Maritime Academy», 9, Fanagoriyskaja Str., Izmail, Odessa Region, 68600-Ukraine

Candidate of Technical Sciences, Associate Professor

Department of Technical Subjects 

References

  1. Faux, I. D., Pratt, M. J. (1982). Computational Geometry for Design and Manufacture. Translated from English. Moscow: Mir, 304.
  2. Zav'ialov, Yu. S., Kvasov, B. I., Miroshnichenko, V. L. (1982). Metody splain-funktsii. Moscow: Nauka, 352.
  3. Kovtun, A. M. (2004). Polinomialni splainy chetvertoho stepenia. Mizhvidomchyi naukovo-tekhnichnyi zbirnyk «Prykladna heometriia ta inzhenerna hrafika», Vol. 74, 239–243.
  4. Golovanov, N. N. (2002). Geometricheskoe modelirovanie. Moscow: Izdatel'stvo fiziko-matematicheskoi literatury, 472.
  5. Badaev, Yu. I., Kovtun, A. M. (2011). Spetsial'nye splainy iz polinomov tret'ei, chetviortoi i piatoi stepenei v geometricheskom modelirovanii. Odessa: Feniks, 316.
  6. Badaev, Yu. I., Kovtun, A. M. (2003). Vektorno-parametrychni sehmenty, poverkhni ta tila za intsydentnymy z nymy tochkamy. Pratsi Tavriiskoi derzhavnoi ahrotekhnichnoi akademii. Prykladna heometriia ta inzhenerna hrafika, Vol. 4, № 18, 37–40.
  7. Csurcsia, P. Z., Schoukens, J., Kollar, I. (2012, May). Identification of time-varying systems using a two-dimensional B-spline algorithm. 2012 IEEE International Instrumentation and Measurement Technology Conference Proceedings. Institute of Electrical and Electronics Engineers (IEEE). Available: https://doi.org/10.1109/i2mtc.2012.6229494
  8. Rogers, D., Adams, J. (2001). Mathematical Elements for Computer Graphics. Translated from English. Moscow: Mir, 604.
  9. Yakunin, V. I. (1980). Geometricheskie osnovy avtomatizirovannogo proektirovaniia tehnicheskih poverhnostei. Moscow: Mai, 86.
  10. Zav'ialov, Yu. S., Leus, V. A., Skorospelov, V. A. (1985). Splainy v inzhenernoi geometrii. Moscow: Mashinostroenie, 224.
  11. Watt, A. (2000). 3D Computer Graphics. Ed. 3. Addison-Wesley, 570.
  12. Zamani, M. (2010). A simple 2D interpolation model for analysis of nonlinear data. Natural Science, Vol. 2, № 6, 641–645. doi:10.4236/ns.2010.26080
  13. Chen, L., Hu, S. (2011, May). A Comparison of Improvements for Shear Warp Algorithm Using Lagrange or Cubic Spline Interpolation. 2011 5th International Conference on Bioinformatics and Biomedical Engineering. Institute of Electrical and Electronics Engineers (IEEE). Available: https://doi.org/10.1109/icbbe.2011.5780354
  14. Herman, G. T., Bucholtz, C. A., Jingsheng Zheng. (1991). Shape-based Interpolation Using Modified Cubic Splines. Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Vol. 13, № 1. Available: https://doi.org/10.1109/iembs.1991.683941
  15. Badaev, Yu. I., Kovtun, A. M. (2003). Aproksymatsiia splainamy na osnovi kryvykh z intsydentnymy tochkamy. Pratsi Natsionalnoho universytetu «Lvivska politekhnika» (spetsvypusk). Materialy mizhnarodnoi naukovo-praktychnoi konferentsii «Suchasni problemy heometrychnoho modeliuvannia». Lviv: Natsionalnyi universytet «Lvivska politekhnika», 75–77.
  16. Moreno, J., Gonzalez, I., Algar, M. J., Catedra, F. (2014, April). Analysis of NURBS dielectric volumes by using the Method of Moments. The 8th European Conference on Antennas and Propagation (EuCAP 2014). Institute of Electrical and Electronics Engineers (IEEE). Available: https://doi.org/10.1109/eucap.2014.6902306
  17. Kovtun, A. M. (2006). Spetsialni polinomialni splainy tretoho, chetvertoho i piatoho stepeniv u heometrychnomu modeliuvanni. Kyiv, 21.

Downloads

Published

2016-09-29

How to Cite

Ковтун, А. М. (2016). Research of algorithm for calculating the vector-parametric bispline based on polynomial of the fourth degree. Technology Audit and Production Reserves, 5(1(31), 22–26. https://doi.org/10.15587/2312-8372.2016.80457

Issue

Vol. 5 No. 1(31) (2016): Mathematical modeling. Mechanical engineering and machine building. Electrical engineering and industrial electronics

Section

Mathematical Modeling: Original Research

License

Copyright (c) 2016 Александр Михайлович Ковтун

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.