Development of oil extraction screening methodology taking into account innovative methods using the example of the Ukrainian field
DOI:
https://doi.org/10.15587/2706-5448.2023.294081Keywords:
irreducible water saturation, representative elementary volume, kriging, relative permeability, fractional flow curves, oil recovery coefficientAbstract
The object of research in the paper is the process of fluid transfer through the pore space of the reservoir rock. The traditional method of estimating oil recovery by flooding has a large number of uncertainties. In this study, to address limitations of the current approach to determining oil production, let’s introduce a systematic algorithm aimed at enhancing result precision.
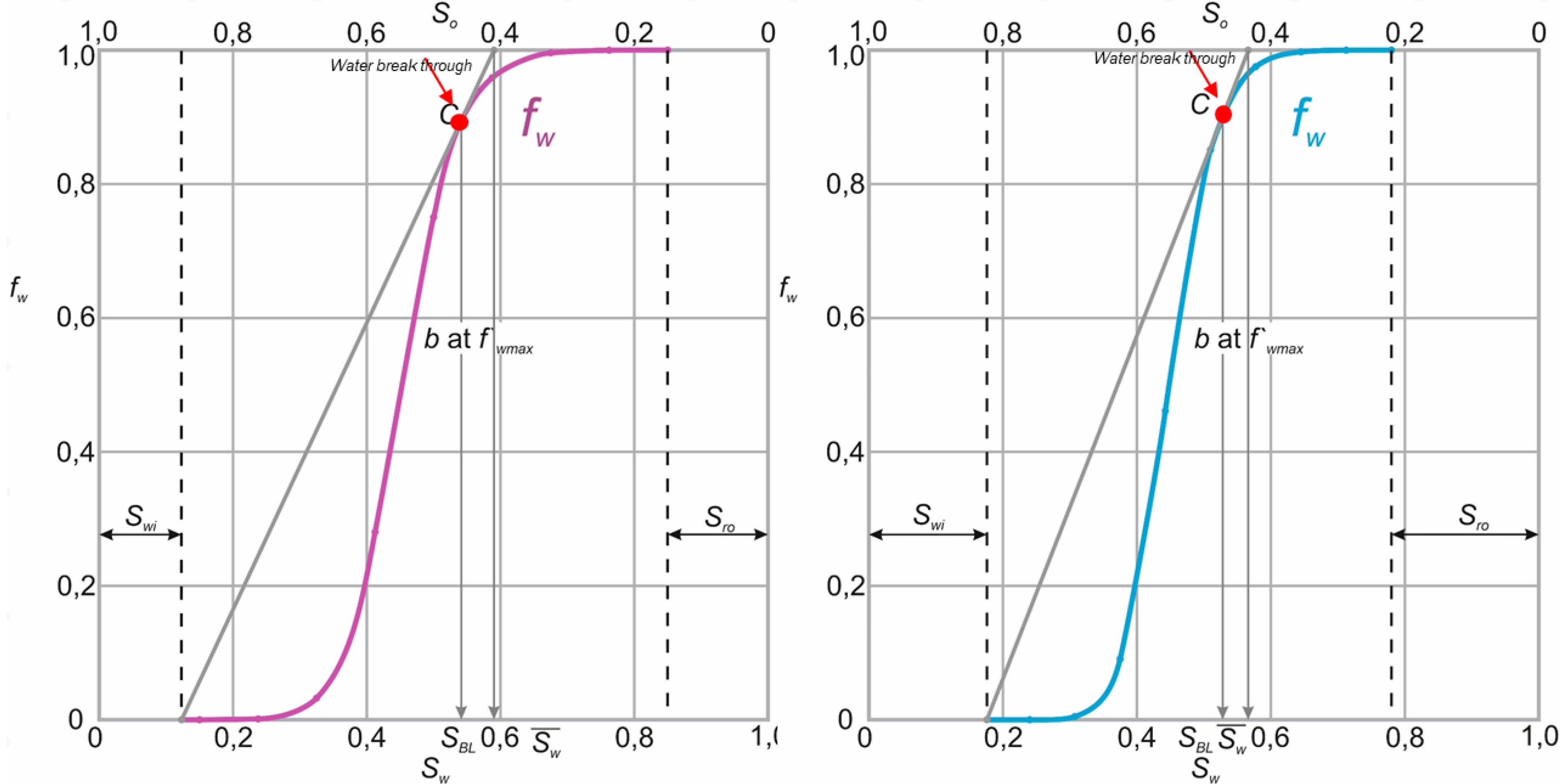
The methodology for calculating the oil recovery coefficient for determining the amount of oil that can be extracted by flooding is presented. In this work, the step-by-step process of determining the oil recovery coefficient was analytically established, which achieves a certain degree of accuracy due to the inclusion of a number of methods of calculation of scientists from different countries of the world. In particular, the lithofacies distribution of the reservoir using the kriging method, the use of a representative elementary volume (REV) to increase the accuracy of determining the irreducible water saturation of each facies, and the use of the Buckley-Leverett equation in the calculation of the oil recovery coefficient are proposed. The number of facies (sandstone, argillaceous sandstone, siltstone) was determined on the example of the B-16n horizon of the «Ukrainian deposit» and the oil recovery coefficients were calculated for each separately (0.53, 0.47, 0.29). Further determination of the average oil recovery coefficient is described in the researched and requires close integration of the obtained data in three-dimensional space, as it allows to calculate the fraction of facies content in the reservoir volume.
The use of the proposed action algorithm will help to build a more reliable three-dimensional hydrodynamic model, will lead to a much lower degree of uncertainty of reservoir properties, and in particular irreducible water saturation, as well as more accurate distribution of lithological properties using kriging. Also, this methodology for calculating the oil recovery coefficient involves the use of the Buckley-Leverett equation and fractional flow curves, the data of which are based on relative permeabilities and depend on the irreducible water saturation determined in the laboratory for each lithofacies.
These techniques justify the collection of additional core material, the importance of lithofacies dismemberment of the formation and are closely integrated in the three-dimensional space, which makes it possible to simulate the existing processes, reproduce the proposed methodology and perform the forecast.
References
- Cvetkovic, B. (2009). Well Production Decline. Available at: https://www.semanticscholar.org/paper/Well-Production-Decline-Cvetkovi%C4%87/7a541f814c78fa6579b510db902cb958b9a3eab0
- Blunt, M. J. (2017). Multiphase flow in permeable media: A pore-scale perspective. Cambridge university press. doi: https://doi.org/10.1017/9781316145098
- Ringrose, P., Bentley, M. (2014). Upscaling Flow Properties. Reservoir Model Design. Berlin: Springer, 115–149. doi: https://doi.org/10.1007/978-94-007-5497-3_4
- Martus, O., Petrash, O. (2022). Improved methodology development for assessing the reservoir collector properties by the quantitative reservoir characterization tools. Technology Audit and Production Reserves, 4 (1 (66)), 42–46. doi: https://doi.org/10.15587/2706-5448.2022.263640
- Martus, O., Agarkov, V. (2022). Development of improved method for evaluation of reservoir properties of formation. Technology Audit and Production Reserves, 5 (1 (67)), 33–37. doi: https://doi.org/10.15587/2706-5448.2022.266572
- Hilfer, R., Lemmer, A. (2015). Differential porosimetry and permeametry for random porous media. Physical Review E, 92 (1). doi: https://doi.org/10.1103/physreve.92.013305
- Bear, J. (2013). Dynamics of fluids in porous media. Courier Corporation.
- Lyons, W. (2010). Working guide to reservoir engineering. Gulf professional publishing. doi: https://doi.org/10.1016/c2009-0-30573-5
- Leverett, M. C. (1941). Capillary Behavior in Porous Solids. Transactions of the AIME, 142 (1), 152–169. doi: https://doi.org/10.2118/941152-g
- Buckley, S. E., Leverett, M. C. (1942). Mechanism of Fluid Displacement in Sands. Transactions of the AIME, 146 (1), 107–116. doi: https://doi.org/10.2118/942107-g
- Willhite, G. P. (1986). Waterflooding. Richardson. doi: https://doi.org/10.2118/9781555630058
- Singh, S. P., Kiel, O. G. (1982). Waterflood design (pattern, rate, and timing). SPE International Oil and Gas Conference and Exhibition in China, SPE-10024. doi: https://doi.org/10.2118/10024-ms
- Forrest, F., Craig, J. (1971). The reservoir engineering aspects of waterflooding. Society of Petroleum.
- Langnes, G. L., Robertson Jr, J. O., Chilingar, G. V. (1972). Secondary recovery and carbonate reservoirs. New York, 305.
- Improved Oil Recovery (1983). Interstate Oil Compact Commission.
- Welge, H. J. (1952). A Simplified Method for Computing Oil Recovery by Gas or Water Drive. Journal of Petroleum Technology, 4 (4), 91–98. doi: https://doi.org/10.2118/124-g
- Lis-Śledziona, A., Stadtmüller, M. (2019). Determining irreducible water saturation based on well log data and laboratory measurements. Nafta-Gaz, 75 (5), 239–246. doi: https://doi.org/10.18668/ng.2019.05.01
- Iske, A., Randen, T. (Eds.) (2006). Mathematical methods and modelling in hydrocarbon exploration and production. Vol. 7. Springer Science & Business Media, 452. doi: https://doi.org/10.1007/b137702
- Kirilov, A. S., Zakrevskii, K. E. (2014). Praktikum po seismicheskoi interpretatcii v PETREL. Moscow.
- Babasafari, A. A., Ghosh, D. P., Ratnam, T., Rezaei, S., Sambo, C. (2022). Geological reservoir modeling and seismic reservoir monitoring. Seismic Imaging Methods and Applications for Oil and Gas Exploration. Elsevier, 179–285. doi: https://doi.org/10.1016/b978-0-323-91946-3.00002-x
- Cosentino, L. (2001). Integrated reservoir studies. Editions Technip, 336.
- Galli, A., Beucher, H., Le Loc’h, G., Doligez, B., Group, H. (1994). The Pros and Cons of the Truncated Gaussian Method. Quantitative Geology and Geostatistics. Springer, 217–233. doi: https://doi.org/10.1007/978-94-015-8267-4_18
- Cornish, B. E., King, G. A. (1988). Combined interactive analysis and stochastic inversion for high-resolution reservoir modeling. 50th Mtg. European Assn. Expl. Geophys.
- Hansen, K. M. (1992). The use of sequential indicator simulation to characterize geostatistical uncertainty (No. SAND--91-0758). Sandia National Labs.
- Matheron, G. (1963). Principles of geostatistics. Economic Geology, 58 (8), 1246–1266. doi: https://doi.org/10.2113/gsecongeo.58.8.1246
- Bohling, G. (2005). Introduction to geostatistics and variogram analysis. Kansas geological survey, 1 (10), 1–20.
- Isaaks, E. H., Srivastava, R. M. (1990). An Introduction to Applied Geostatistics. Oxford University Press, 592.
- Pyrcz, M. J., Deutsch, C. V. (2014). Geostatistical reservoir modeling. Oxford University Press.
- Cressie, N. (2015). Statistics for spatial data. John Wiley & Sons.
Downloads
Published
How to Cite
Issue
Section
License
Copyright (c) 2023 Olena Martus, Branimir Cvetkovic

This work is licensed under a Creative Commons Attribution 4.0 International License.
The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.







