Development of the hardness mathematical model of Ti-alloyed iron for cast parts used in conditions of intensive abrasive friction

Authors

DOI:

https://doi.org/10.15587/2706-5448.2024.301156

Keywords:

wear resistance of cast iron, HRC hardness, alloying of cast iron, chemical composition of cast iron

Abstract

The object of research is wear-resistant cast iron, intended for cast parts that work under conditions of intense abrasive friction during operation. Examples of such parts can be mixer blades of various functional purposes, the operational properties of which include stability, which depends on the hardness, determined on the HRC scale. To give such cast parts wear-resistant properties, the cast iron from which they are made is alloyed with elements that contribute to the formation of carbides of different composition: W, V, Mo, Ti, etc. The main problem that prevents the purposeful selection of materials is incomplete knowledge about the effect of chemical composition on properties, in particular, wear resistance, which prevents a justified selection criterion.

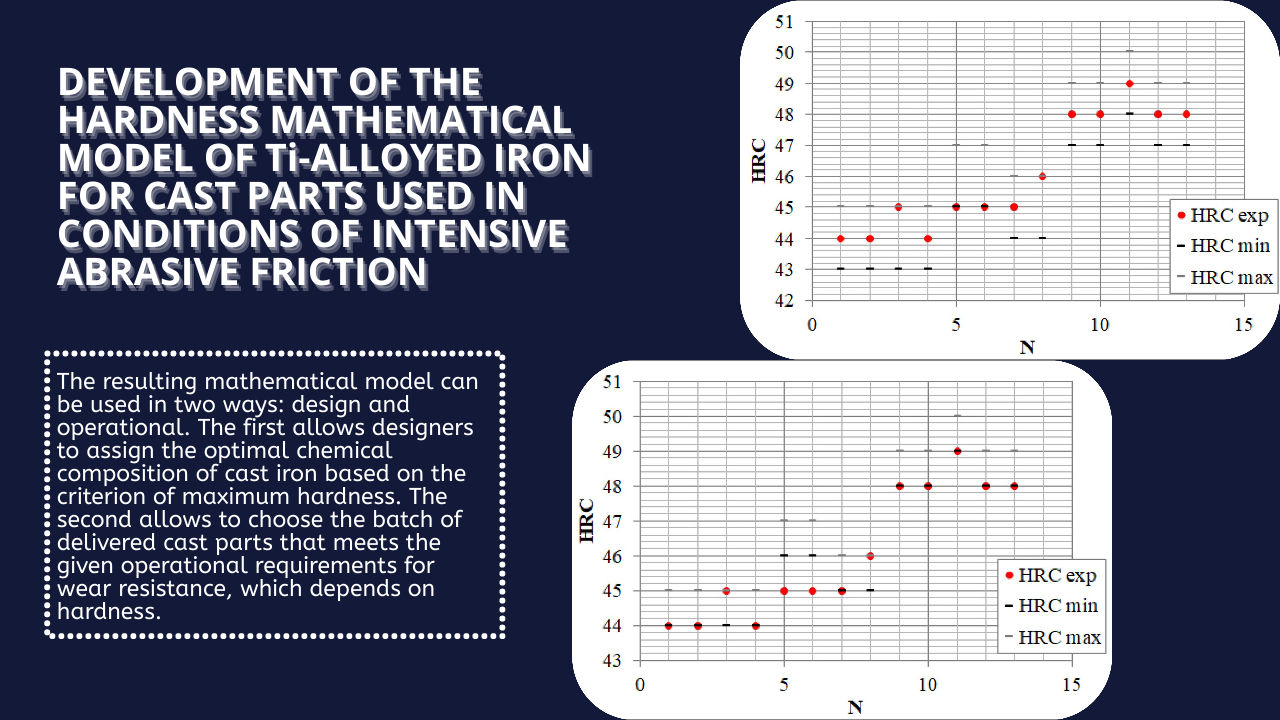
Using regression analysis methods, a mathematical model was obtained, including a regression equation of the form HRC=f(C; Ceq; Ti), which relates the content of carbon, titanium and carbon equivalent in cast iron and hardness. The resulting model allows for purposeful selection of the chemical composition, which ensures a given value of HRC, on which wear resistance depends. Optimization of the chemical composition, performed according to this model, made it possible to determine that the chemical composition, which provides the maximum hardness of HRC=49, is outside the planning area: C=3.54 %, Ceq=3.95 %, Ti=3.56 %. It was established that the same value of hardness can be obtained inside the considered planning area, which has an arbitrary appearance, provided with available conditions of a passive experiment. According to the available experimental data, the values of the input variables equal to C=3.34 %, Ceq=3.727 %, Ti=0.73 % ensure obtaining hardness at the level of HRC=49. Such alternative options regarding composition and properties may indicate that the HRC=f(C; Ceq; Ti) response surface has a complex appearance that requires additional research.

Author Biography

Andriy Barsuk, National Technical University «Kharkiv Polytechnic Institute»

Postgraduate Student

Department of Foundry Production

References

  1. Golub, G., Myhailovych, Y., Achkevych, O., Chuba, V. (2019). Optimization of angular velocity of drum mixers. Eastern-European Journal of Enterprise Technologies, 3 (7 (99)), 64–72. doi: https://doi.org/10.15587/1729-4061.2019.166944
  2. Hassanpour, A., Tan, H., Bayly, A., Gopalkrishnan, P., Ng, B., Ghadiri, M. (2011). Analysis of particle motion in a paddle mixer using Discrete Element Method (DEM). Powder Technology, 206 (1-2), 189–194. doi: https://doi.org/10.1016/j.powtec.2010.07.025
  3. Gao, W., Liu, L., Liao, Z., Chen, S., Zang, M., Tan, Y. (2019). Discrete element analysis of the particle mixing performance in a ribbon mixer with a double U-shaped vessel. Granular Matter, 21 (1). doi: https://doi.org/10.1007/s10035-018-0864-4
  4. Bohl, D., Mehta, A., Santitissadeekorn, N., Bollt, E. (2011). Characterization of Mixing in a Simple Paddle Mixer Using Experimentally Derived Velocity Fields. Journal of Fluids Engineering, 133 (6). doi: https://doi.org/10.1115/1.4004086
  5. Li, S., Kajiwara, S., Sakai, M. (2021). Numerical investigation on the mixing mechanism in a cross-torus paddle mixer using the DEM-CFD method. Powder Technology, 377, 89–102. doi: https://doi.org/10.1016/j.powtec.2020.08.085
  6. Zaselskiy, V., Shved, S., Shepelenko, M., Suslo, N. (2020). Modeling the horizontal movement of bulk material in the system «conveyor – rotary mixer». E3S Web of Conferences, 166, 06008. doi: https://doi.org/10.1051/e3sconf/202016606008
  7. Demin, D. A., Pelikh, V. F., Ponomarenko, O. I. (1995). Optimization of the method of adjustment of chemical composition of flake graphite iron. Litejnoe Proizvodstvo, 7-8, 42–43.
  8. Demin, D. A. (1998). Change in cast iron's chemical composition in inoculation with a Si-V-Mn master alloy. Litejnoe Proizvodstvo, 6, 35.
  9. Frolova, L., Barsuk, A., Nikolaiev, D. (2022). Revealing the significance of the influence of vanadium on the mechanical properties of cast iron for castings for machine-building purpose. Technology Audit and Production Reserves, 4 (1 (66)), 6–10. doi: https://doi.org/10.15587/2706-5448.2022.263428
  10. Demin, D. (2017). Strength analysis of lamellar graphite cast iron in the «carbon (C) – carbon equivalent (Ceq)» factor space in the range of C=(3,425-3,563) % and Ceq=(4,214-4,372) %. Technology Audit and Production Reserves, 1 (1 (33)), 24–32. doi: https://doi.org/10.15587/2312-8372.2017.93178
  11. Demin, D. (2017). Synthesis of nomogram for the calculation of suboptimal chemical composition of the structural cast iron on the basis of the parametric description of the ultimate strength response surface. ScienceRise, 8, 36–45. doi: https://doi.org/10.15587/2313-8416.2017.109175
  12. Demin, D. (2018). Investigation of structural cast iron hardness for castings of automobile industry on the basis of construction and analysis of regression equation in the factor space «carbon (C) – carbon equivalent (Ceq)». Technology Audit and Production Reserves, 3 (1 (41)), 29–36. doi: https://doi.org/10.15587/2312-8372.2018.109097
  13. Mohanad, M. K., Kostyk, V., Domin, D., Kostyk, K. (2016). Modeling of the case depth and surface hardness of steel during ion nitriding. Eastern-European Journal of Enterprise Technologies, 2 (5 (80)), 45–49. doi: https://doi.org/10.15587/1729-4061.2016.65454
  14. Kontorov, B. M., Kunin, N. M. (1960). Iznosostoikie belye chuguny, legirovany borom i titanom. Liteinoe proizvodstvo, 4.
  15. Demin, D. (2020). Constructing the parametric failure function of the temperature control system of induction crucible furnaces. EUREKA: Physics and Engineering, 6, 19–32. doi: https://doi.org/10.21303/2461-4262.2020.001489
  16. Kharchenko, S., Barsuk, A., Karimova, N., Nanka, A., Pelypenko, Y., Shevtsov, V. et al. (2021). Mathematical model of the mechanical properties of Ti-alloyed hypoeutectic cast iron for mixer blades. EUREKA: Physics and Engineering, 3, 99–110. doi: https://doi.org/10.21303/2461-4262.2021.001830
  17. Barsuk, A. (2022). Optimization of the composition of cast iron for cast parts operating under abrasive friction, according to the criterion of maximum wear resistance. ScienceRise, 5, 14–20. doi: https://doi.org/10.21303/2313-8416.2022.002775
  18. Domin, D. (2013). Artificial orthogonalization in searching of optimal control of technological processes under uncertainty conditions. Eastern-European Journal of Enterprise Technologies, 5 (9 (65)), 45–53. doi: https://doi.org/10.15587/1729-4061.2013.18452
Development of the hardness mathematical model of Ti-alloyed iron for cast parts used in conditions of intensive abrasive friction

Downloads

Published

2024-04-03

How to Cite

Barsuk, A. (2024). Development of the hardness mathematical model of Ti-alloyed iron for cast parts used in conditions of intensive abrasive friction. Technology Audit and Production Reserves, 3(1(77), 6–9. https://doi.org/10.15587/2706-5448.2024.301156

Issue

Vol. 3 No. 1(77) (2024): Industrial and technology systems

Section

Metallurgical Technology

License

Copyright (c) 2024 Andriy Barsuk

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.