Testing the suitability of vector normalization procedure in topsis method: application to wheel loader selection

Authors

DOI:

https://doi.org/10.15587/2706-5448.2024.301207

Keywords:

multi-criteria decision-making, wheel loader selection, normalization procedures, TOPSIS, statistical approach

Abstract

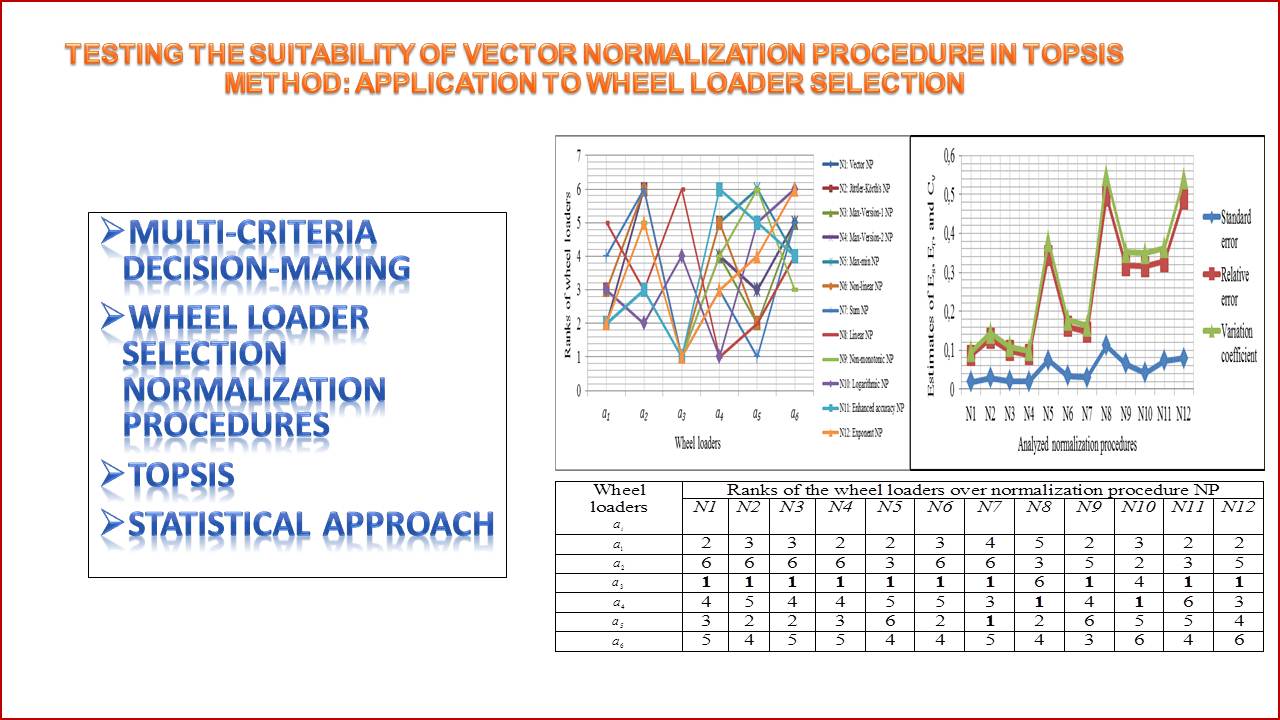
The object of the research consists of testing the suitability of the vector normalization procedure (NP) in the Technique for Order Preference by Similarity to the Ideal Solution (TOPSIS) method. One of the most problematic steps of the Multi-Criteria Decision Making (MCDM) process is related to the application of NPs by default to transform different measurement units of criteria into a comparable unit. This is because of the absence of a universal agreement that defines which NP is the most suitable for a given MCDM method. In the literature, there are thirty-one available NPs, each one of them has its strengths and weaknesses and, accordingly, can efficiently be applied to an MCDM method and even worst to another. Let’s note that many NPs (e. g., NPs of sum, max-min, vector, and max) have been used by default (i. e., without suitability study) in the TOPSIS method. Consequently, outcomes of multi-criteria evaluation and rankings of alternatives considered in the decision problems could have led to inconsistent solutions, and, therefore, decision-makers could have made irrational or inappropriate decisions. That’s why suitability studies of NPs become indispensable. Moreover, a description of the methodology, proposed in this research, is outlined as follows:

1) method of weighting based on an ordinal ranking of criteria and Lagrange multiplier (for determining criteria weights);

2) TOPSIS method (for ranking considered alternatives);

3) a statistical approach with 3-estimate (for comparing effects generated by the used NPs).

In the research, twelve different NPs are compared to each other in the TOPSIS method via a numerical example, which deals with the wheel loader selection problem. The results of the comparison indicate that, amongst the twelve different NPs analyzed in this suitability study, vector NP has the lesser effect on the considered alternatives’ evaluation outcomes, when used with the TOPSIS method. The vector NP-TOPSIS approach can therefore be applied to solve multi-criteria decision problems. Its application further allows the decision-makers and users to better select efficient solutions and, consequently, to make conclusive decisions.

Author Biographies

Mohamed Bouhedja, University of Badji Mokhtar

Department of Mathematics

 

Samir Bouhedja, University of Sciences and Technology – Houari Boumediene

Doctor of Civil Engineering, Senior Lecturer

Laboratory of Environment, Water, Geomechanics, and Structures

 

Aissa Benselhoub, Environment, Modeling and Climate Change Division

PhD, Associate Researcher

Environmental Research Center

 

References

  1. Saaty, T. L., Ergu, D. (2015). When is a Decision-Making Method Trustworthy? Criteria for Evaluating Multi-Criteria Decision-Making Methods. International Journal of Information Technology & Decision Making, 14 (6), 1171–1187. doi: https://doi.org/10.1142/s021962201550025x
  2. Roberts, F. S. (1979). Measurement theory – Encyclopedia of mathematics and its applications. Boston: Addisson-Wesly.
  3. Pomerol, J. C., Barba-Romeo, S. (1993). Multi-criteria choice in the enterprise: Principles and practice. Paris: Hermès Edition.
  4. Zavadskas, E. K., Turskis, Z. (2008). A New Logarithmic Normalization Method in Games Theory. Informatica, 19 (2), 303–314. doi: https://doi.org/10.15388/informatica.2008.215
  5. Tofallis, C. (2014). Add or Multiply? A Tutorial on Ranking and Choosing with Multiple Criteria. INFORMS Transactions on Education, 14 (3), 109–119. doi: https://doi.org/10.1287/ited.2013.0124
  6. Pavlicic, D. (2000). Normalization of attribute values in MADM violates the conditions of consistent choice. Yugoslav Journal of Operations Research, 10 (1), 109–122.
  7. Pavlicic, D. (2001). Normalization affects the results of MADM methods. Yugoslav Journal of Operations Research, 11 (2), 251–265.
  8. Mokotoff, E., Garcia-Vázquez, E., Pérez-Navarro, J. (2010). Normalization procedures on multi-criteria decision making: An example on environment problems. 12th International Conference on Enterprise Information Systems – Artificial Intelligence and Decision Support Systems. Portugal, 206–2011. doi: https://doi.org/10.5220/0002896102060211
  9. Eftekhary, M., Gholami, P., Safari, S., Shojaee, M. (2012). Ranking Normalization Methods for Improving the Accuracy of SVM Algorithm by DEA Method. Modern Applied Science, 6 (10). doi: https://doi.org/10.5539/mas.v6n10p26
  10. Yazdani, M., Jahan, A., Zavadskas, E. K. (2017). Analysis in material selection: Influence of normalization tools on COPRAS-G. Economic Computation and Economic Cybernetics Studies and Research, 51 (1), 59–74.
  11. Palczewski, K., Sałabun, W. (2019). Influence of various normalization methods in PROMETHEE II: an empirical study on the selection of the airport location. Procedia Computer Science, 159, 2051–2060. doi: https://doi.org/10.1016/j.procs.2019.09.378
  12. Milani, A. S., Shanian, A., Madoliat, R., Nemes, J. A. (2004). The effect of normalization norms in multiple attribute decision making models: a case study in gear material selection. Structural and Multidisciplinary Optimization, 29 (4), 312–318. doi: https://doi.org/10.1007/s00158-004-0473-1
  13. Zavadskas, E. K., Zakarevicius, A., Antucheviciene, J. (2006). Evaluation of Ranking Accuracy in Multi-Criteria Decisions. Informatica, 17 (4), 601–618. doi: https://doi.org/10.15388/informatica.2006.158
  14. Chakraborty, S., Yeh, C. H. (2009). A simulation comparison of normalization procedures for TOPSIS. International Conference on Computers and Industrial Engineering, France, Troyes, Proceedings, 1815–1820. doi: https://doi.org/10.1109/iccie.2009.5223811
  15. Liao, Y., Liu, L., Xing, C. (2012). Investigation of different normalization methods for TOPSIS. Transactions of Beijing – Institute of Technology, 32 (5), 871–875.
  16. Özdağoğlu, A. (2013). The effects of different normalization methods to decision making process in TOPSIS. EGE Academic Review, 13 (2), 245–257.
  17. Salabun, W. (2013). The mean error estimation of TOPSIS method using a fuzzy reference models. Journal of Theoretical and Applied Computer Science, 7 (3), 40–50.
  18. Çelen, A. (2014). Comparative Analysis of Normalization Procedures in TOPSIS Method: With an Application to Turkish Deposit Banking Market. Informatica, 25 (2), 185–208. doi: https://doi.org/10.15388/informatica.2014.10
  19. Chatterjee, P., Chakraborty, S. (2014). Investigating the Effect of Normalization Norms in Flexible Manufacturing Sytem Se-lection Using Multi – Criteria Decision – Making Methods. Journal of Engineering Science and Technology Review, 7 (3), 141–150. doi: https://doi.org/10.25103/jestr.073.23
  20. Lakshmi, T. M., Venkatesan, V. P. (2014). A Comparison of Various Normalization in Techniques for Order Performance by Similarity to Ideal Solution (TOPSIS). International Journal of Computing Algorithm, 3 (3), 255–259. doi: https://doi.org/10.20894/ijcoa.101.003.003.023
  21. Podviezko, A., Podvezko, V. (2015). Influence of Data Transformation on Multicriteria Evaluation Result. Procedia Engineering, 122, 151–157. doi: https://doi.org/10.1016/j.proeng.2015.10.019
  22. Aires, R. F. D. F., Ferreira, L. (2016). Rank reversal in TOPSIS method: A comparative analysis of normalization procedures. Brazilian Symposium on Operational Research, 48, 448–459.
  23. Vafaei, N., Ribeiro, R. A., Matos, L. M. C. (2018). Data normalisation techniques in decision making: case study with TOPSIS method. International Journal of Information and Decision Sciences, 10 (1), 19–38. doi: https://doi.org/10.1504/ijids.2018.090667
  24. Jafaryeganeh, H., Ventura, M., Guedes Soares, C. (2020). Effect of normalization techniques in multi-criteria decision making methods for the design of ship internal layout from a Pareto optimal set. Structural and Multidisciplinary Optimization, 62 (4), 1849–1863. doi: https://doi.org/10.1007/s00158-020-02581-9
  25. Krishnan, A. R., Hamid, M. R., Tanakinjal, G. H., Asli, M. F., Boniface, B., Ghazali, M. F. (2023). An investigation to offer conclusive recommendations on suitable benefit/cost criteria-based normalization methods for TOPSIS. MethodsX, 10, 102227. doi: https://doi.org/10.1016/j.mex.2023.102227
  26. Bauer, P. W., Berger, A. N., Ferrier, G. D., Humphrey, D. B. (1998). Consistency Conditions for Regulatory Analysis of Financial Institutions: A Comparison of Frontier Efficiency Methods. Journal of Economics and Business, 50 (2), 85–114. doi: https://doi.org/10.1016/s0148-6195(97)00072-6
  27. Bouhedja, A., Pousin, J. (2017). A new method for determining the weights in multi-criteria decision making based on ordinal ranking of criteria and Lagrange multiplier. Metallurgical and Mining Industry, 5 (1), 22–31.
  28. Hwang, C. L., Yoon, K. (1981). Multiple attribute decision making: Methods and applications. Berlin: Springer – Verlag. doi: https://doi.org/10.1007/978-3-642-48318-9
  29. Bouhedja, S., Boukhaled, A., Bouhedja, A., Benselhoub, A. (2020). Use of the TOPSIS technique to choose the best supplier of quarry natural aggregate. Mining of Mineral Deposits, 14 (1), 11–18. doi: https://doi.org/10.33271/mining14.01.011
  30. Tzeng, G.-H., Chen, T.-Y., Wang, J.-C. (1998). A weight-assessing method with habitual domains. European Journal of Operational Research, 110 (2), 342–367. doi: https://doi.org/10.1016/s0377-2217(97)00246-4
  31. Yeh, C. (2003). The Selection of Multiattribute Decision Making Methods for Scholarship Student Selection. International Journal of Selection and Assessment, 11 (4), 289–296. doi: https://doi.org/10.1111/j.0965-075x.2003.00252.x
  32. Vyas Gayatri, S., Misal Chetan, S. (2013). Comparative study of different multi-criteria decision-making methods. International Journal on Advanced Computer Theory and Engineering, 2 (4), 9–12.
  33. Velasquez, M., Hester, P. T. (2013). An analysis of multi-criteria decision making methods. International Journal of Operations Research, 10 (2), 56–66.
  34. Shih, H.-S., Shyur, H.-J., Lee, E. S. (2007). An extension of TOPSIS for group decision making. Mathematical and Computer Modelling, 45 (7-8), 801–813. doi: https://doi.org/10.1016/j.mcm.2006.03.023
  35. Opricovic, S., Tzeng, G.-H. (2004). Compromise solution by MCDM methods: A comparative analysis of VIKOR and TOPSIS. European Journal of Operational Research, 156 (2), 445–455. doi: https://doi.org/10.1016/s0377-2217(03)00020-1
  36. Stanujkić, D., Đorđević, B., Đorđević, M. (2013). Comparative analysis of some prominent MCDM methods: A case of ranking Serbian banks. Serbian Journal of Management, 8 (2), 213–241. doi: https://doi.org/10.5937/sjm8-3774
  37. Yoon, K., Hwang, C.-L. (1985). Manufacturing plant location analysis by multiple attribute decision making: part I – single-plant strategy. International Journal of Production Research, 23 (2), 345–359. doi: https://doi.org/10.1080/00207548508904712
  38. Batanovic, V.; Colson, G., De Bruin, C. (Eds.) (1989). Multicriteria evaluation of an urban traffic control system: Belgrade case study. Models and Methods in multiple criteria decision making. Pergamon Press, 1411–1417. doi: https://doi.org/10.1016/b978-0-08-037938-8.50021-5
  39. Figueira, J., Greco, S., Ehrgott, M. (2005). Multiple criteria decision analysis: State of the art survey. Boston: Springer. doi: https://doi.org/10.1007/b100605
  40. Alias, M. A., Hashim, S. Z. M., Samsudin, S. (2008). Multi-criteria decision making and its applications: Literature review. Jurnal Teknologi Maklumat, 20 (2), 129–152.
  41. Tzeng, G. H., Huang, J. J. (2011). Multiple attribute decision making. New York: CRC Press. doi: https://doi.org/10.1201/b11032
  42. Behzadian, M., Khanmohammadi Otaghsara, S., Yazdani, M., Ignatius, J. (2012). A state-of the-art survey of TOPSIS applications. Expert Systems with Applications, 39 (17), 13051–13069. doi: https://doi.org/10.1016/j.eswa.2012.05.056
  43. Zavadskas, E. K., Turskis, Z., Kildienė, S. (2014). State of art surveys of overviews on mcdm/madm methods. Technological and Economic Development of Economy, 20 (1), 165–179. doi: https://doi.org/10.3846/20294913.2014.892037
  44. Mardani, A., Jusoh, A., Nor, K., Khalifah, Z., Zakwan, N., Valipour, A. (2015). Multiple criteria decision-making techniques and their applications – a review of the literature from 2000 to 2014. Economic Research-Ekonomska Istraživanja, 28 (1), 516–571. doi: https://doi.org/10.1080/1331677x.2015.1075139
  45. Zavadskas, E. K., Govindan, K., Antucheviciene, J., Turskis, Z. (2016). Hybrid multiple criteria decision-making methods: a review of applications for sustainability issues. Economic Research-Ekonomska Istraživanja, 29 (1), 857–887. doi: https://doi.org/10.1080/1331677x.2016.1237302
  46. Sitorus, F., Cilliers, J. J., Brito-Parada, P. R. (2019). Multi-criteria decision making for the choice problem in mining and mineral processing: Applications and trends. Expert Systems with Applications, 121, 393–417. doi: https://doi.org/10.1016/j.eswa.2018.12.001
  47. Ross, S. M. (2014). Introduction to probability and statistics for engineers and scientists. Academic Press Publications of Elsevier Incorporation. doi: https://doi.org/10.1016/c2013-0-19397-x
  48. Chouafa, M., Idres, A., Bouhedja, A., Talhi, K. (2015). Chemical treatment of Kaolin: Case study of Kaolin from the Tamazert-Jijel mine. Mining Science, 22 (1), 173–182. doi: https://doi.org/10.5277/msc152214
  49. Zha, S., Guo, Y., Huang, S., Wang, S. (2020). A Hybrid MCDM Method Using Combination Weight for the Selection of Facility Layout in the Manufacturing System: A Case Study. Mathematical Problems in Engineering, 2020, 1–16. doi: https://doi.org/10.1155/2020/1320173
  50. Jahan, A., Edwards, K. L. (2015). A state-of-the-art survey on the influence of normalization techniques in ranking: Improving the materials selection process in engineering design. Materials & Design (1980-2015), 65, 335–342. doi: https://doi.org/10.1016/j.matdes.2014.09.022
  51. Van Delft, A., Nijkamp, P. (1977). Multi-criteria analysis and regional decision making. Leiden: Martinus Nijhoft Publishing.
  52. Körth, H. (1969). Taking into account multiple objective functions when optimizing production planning. Mathematics and Economics, 6, 184–201.
  53. Stopp, F. (1975). Variants comparison through matrix games. Journal of Leipzig Civil Engineering Institute, Brochure 2, 117.
  54. Farag, M. M. (1997). Materials selection for engineering design. London: Prentice Hall.
  55. Weitendorf, D. (1976). Contribution to optimizing the spatial structure of a building. Institute of Architecture and Construction. Weimar.
  56. Peldschus, F., Vaigauskas, E., Zavadskas, E. K. (1983). Technological decisions when taking into account multiple goals. Construction Planning – Construction Technology, 37 (4), 173–175.
  57. Lai, Y. J., Hwang, C. L. (1994). Fuzzy multiple objective decision making: Methods and applications. Berlin: Springer-Verlag. doi: https://doi.org/10.1007/978-3-642-57949-3_3
  58. Zeng, Q.-L., Li, D.-D., Yang, Y.-B. (2013). VIKOR Method with Enhanced Accuracy for Multiple Criteria Decision Making in Healthcare Management. Journal of Medical Systems, 37 (2). doi: https://doi.org/10.1007/s10916-012-9908-1
  59. Vavrek, R. (2019). Evaluation of the Impact of Selected Weighting Methods on the Results of the TOPSIS Technique. International Journal of Information Technology & Decision Making, 18 (6), 1821–1843. doi: https://doi.org/10.1142/s021962201950041x
  60. Huang, J.-H., Peng, K.-H. (2012). Fuzzy Rasch model in TOPSIS: A new approach for generating fuzzy numbers to assess the competitiveness of the tourism industries in Asian countries. Tourism Management, 33 (2), 456–465. doi: https://doi.org/10.1016/j.tourman.2011.05.006
Testing the suitability of vector normalization procedure in topsis method: application to wheel loader selection

Downloads

Published

2024-04-16

How to Cite

Bouhedja, M., Bouhedja, S., & Benselhoub, A. (2024). Testing the suitability of vector normalization procedure in topsis method: application to wheel loader selection. Technology Audit and Production Reserves, 2(2(76), 52–62. https://doi.org/10.15587/2706-5448.2024.301207

Issue

Vol. 2 No. 2(76) (2024): Information and control systems

Section

Mathematical Modeling

License

Copyright (c) 2024 Mohamed Bouhedja, Samir Bouhedja, Aissa Benselhoub

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.