Development of the stick-slip friction model for discrete elements modeling

Authors

DOI:

https://doi.org/10.15587/2706-5448.2024.310428

Keywords:

Coulomb friction, static, dynamic, stick-slip, discrete element method, soft contact, shear rate

Abstract

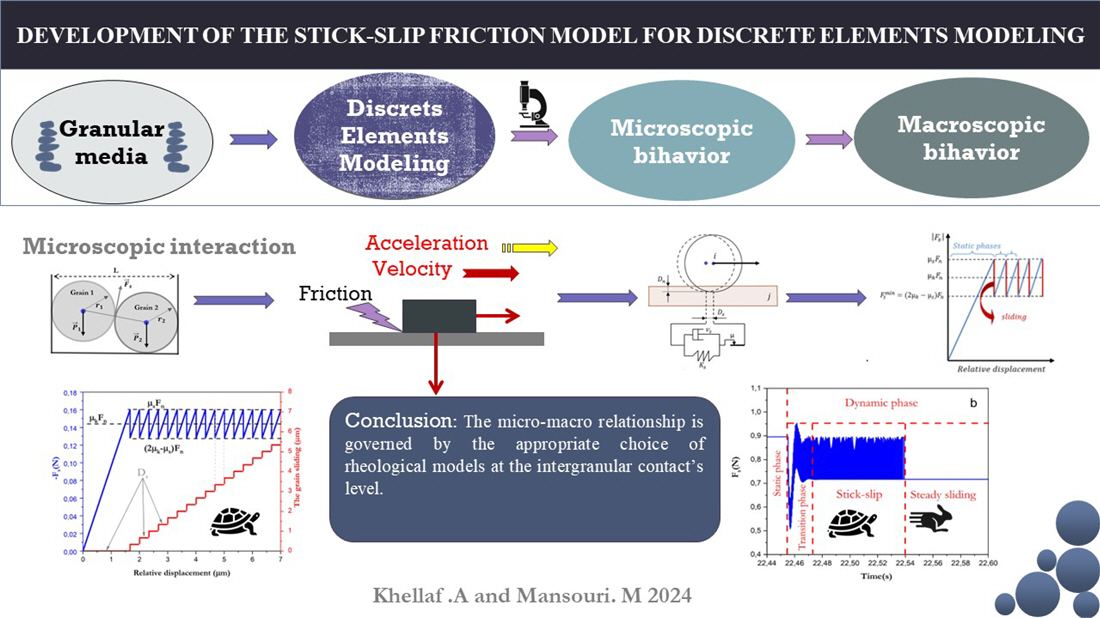
The object of the research is an intergranular friction model for use in discrete-element modeling of the mechanical behavior of granular materials under static and dynamic conditions. As in this approach grains are modeled by independent elements interacting through contact forces, the selection of contact force models, and in particular for the tangential component (friction), represents the most important task in obtaining the most realistic macroscopic behavior. There are many friction models that work well in dynamic regimes, but fail to model mechanical behavior in static or quasi-static regimes. In this work, an intergranular friction model is proposed based on Coulomb's regularized friction model, which takes into account the stick-slip phenomenon that appears at low sliding speeds at the contact. Three different examples are designed and modeled in order to demonstrate the robustness of the model in different situations including static, quasi-static and dynamic regimes. The first is a basic example consisting of the translational motion of a grain on a planar surface with a relatively low constant velocity. This example allowed to capture the stick-slip phenomenon. The second represents a grain subjected to its own weight and supported essentially by frictional forces. This example shows that the model works well in both quasi-static and static regimes. The third example consists of a grain sliding on a plate and subjected to accelerated motion. It showed the effect of friction velocity on the occurrence of stick-slip, as well as the evolution of friction force with sliding velocity. The obtained results demonstrated that the model effectively captures shear behavior in the different regimes. It could therefore be used in discrete element modeling of granular materials under both static and dynamic conditions. As in this work, the model is formulated in 2D, it would be interesting to develop a general 3D formulation so that it can be easily applied in 3D modeling.

Author Biographies

Abdelghani Khellaf, Ferhat Abbas University Setif 1

PhD Student

Department of Civil Engineering

Mouloud Mansouri, Ferhat Abbas University Setif 1

MCA Dr.

Department of Civil Engineering

References

  1. Cundall, P. A., Strack, O. D. L. (1979). A discrete numerical model for granular assemblies. Géotechnique, 29 (1), 47–65. https://doi.org/10.1680/geot.1979.29.1.47
  2. Hong, D. C., McLennan, J. A. (1992). Molecular dynamics simulations of hard sphere granular particles. Physica A: Statistical Mechanics and Its Applications, 187 (1-2), 159–171. https://doi.org/10.1016/0378-4371(92)90416-n
  3. Jean, M. (1999). The non-smooth contact dynamics method. Computer Methods in Applied Mechanics and Engineering, 177 (3-4), 235–257. https://doi.org/10.1016/s0045-7825(98)00383-1
  4. Haff, P. K., Werner, B. T. (1986). Computer simulation of the mechanical sorting of grains. Powder Technology, 48 (3), 239–245. https://doi.org/10.1016/0032-5910(86)80048-1
  5. Kruggel-Emden, H., Simsek, E., Rickelt, S., Wirtz, S., Scherer, V. (2007). Review and extension of normal force models for the Discrete Element Method. Powder Technology, 171 (3), 157–173. https://doi.org/10.1016/j.powtec.2006.10.004
  6. Malone, K. F., Xu, B. H. (2008). Determination of contact parameters for discrete element method simulations of granular systems. Particuology, 6 (6), 521–528. https://doi.org/10.1016/j.partic.2008.07.012
  7. Machado, M., Moreira, P., Flores, P., Lankarani, H. M. (2012). Compliant contact force models in multibody dynamics: Evolution of the Hertz contact theory. Mechanism and Machine Theory, 53, 99–121. https://doi.org/10.1016/j.mechmachtheory.2012.02.010
  8. Suhr, B., Six, K. (2016). Friction phenomena and their impact on the shear behaviour of granular material. Computational Particle Mechanics, 4 (1), 23–34. https://doi.org/10.1007/s40571-016-0119-2
  9. Filippo, M., Di Felice, R. (2021). On the Influence of Contact Models on Friction Forces in Discrete Element Method Simulations. Chemical Engineering Transactions, 86, 811–816.
  10. Man, T., Zhang, P., Ge, Z., Galindo-Torres, S. A., Hill, K. M. (2022). Friction-dependent rheology of dry granular systems. Acta Mechanica Sinica, 39 (1). https://doi.org/10.1007/s10409-022-22191-x
  11. Luding, S., Clément, E., Blumen, A., Rajchenbach, J., Duran, J. (1994). Onset of convection in molecular dynamics simulations of grains. Physical Review E, 50 (3), R1762–R1765. https://doi.org/10.1103/physreve.50.r1762
  12. Luding, S. (2008). Cohesive, frictional powders: contact models for tension. Granular Matter, 10 (4), 235–246. https://doi.org/10.1007/s10035-008-0099-x
  13. Führer, F., Brendel, L., Wolf, D. E. (2024). Correction of the spring-dashpot-slider model. Granular Matter, 26 (2). https://doi.org/10.1007/s10035-024-01424-4
  14. Mindlin (1949). Compliance Of Elastic Bodies In Contact. Available at: https://www.researchgate.net/profile/Valentin-Popov-2/post/Does-anyone-have-an-electronic-copy-of-1949-paper-by-Mindlin-Compliance-of-Elastic-Bodies-in-Contact-JAM-16-1949/attachment/5fcfedf53b21a2000160b8d3/AS%3A966581471440897%401607462389742/download/Mindlin_1949_ComplianceOfElasticBodiesInContact.pdf
  15. Walton, O. R., Braun, R. L. (1986). Viscosity, granular‐temperature, and stress calculations for shearing assemblies of inelastic, frictional disks. Journal of Rheology, 30 (5), 949–980. https://doi.org/10.1122/1.549893
  16. Shäfer, J., Dippel, S., Wolf, D. E. (1996). Force Schemes in Simulations of Granular Materials. Journal de Physique I, 6 (1), 5–20. https://doi.org/10.1051/jp1:1996129
  17. Heslot, F., Baumberger, T., Perrin, B., Caroli, B., Caroli, C. (1994). Creep, stick-slip, and dry-friction dynamics: Experiments and a heuristic model. Physical Review E, 49 (6), 4973–4988. https://doi.org/10.1103/physreve.49.4973
  18. Bengisu, M. T., Akay, A. (1999). Stick–slip oscillations: Dynamics of friction and surface roughness. The Journal of the Acoustical Society of America, 105 (1), 194–205. https://doi.org/10.1121/1.424580
  19. Togo, T., Shimamoto, T. (2012). Energy partition for grain crushing in quartz gouge during subseismic to seismic fault motion: An experimental study. Journal of Structural Geology, 38, 139–155. https://doi.org/10.1016/j.jsg.2011.12.014
  20. Persson, B. N. J. (2013). Sliding Friction: Physical Principles and Applications. Springer Science & Business Media.
  21. Berman, A. D., Ducker, W. A., Israelachvili, J. N. (1996). Origin and Characterization of Different Stick−Slip Friction Mechanisms. Langmuir, 12 (19), 4559–4563. https://doi.org/10.1021/la950896z
  22. Dunham, E. M., Rice, J. R. (2008). Earthquake slip between dissimilar poroelastic materials. Journal of Geophysical Research: Solid Earth, 113 (B9). https://doi.org/10.1029/2007jb005405
  23. Singh, T. N., Verma, A. K., Kumar, T., Dutt, A. (2011). Influence of shear velocity on frictional characteristics of rock surface. Journal of Earth System Science, 120 (1), 183–191. https://doi.org/10.1007/s12040-011-0009-1
  24. Yang, C.-M., Yu, W.-L., Dong, J.-J., Kuo, C.-Y., Shimamoto, T., Lee, C.-T., Togo, T., Miyamoto, Y. (2014). Initiation, movement, and run-out of the giant Tsaoling landslide – What can we learn from a simple rigid block model and a velocity–displacement dependent friction law? Engineering Geology, 182, 158–181. https://doi.org/10.1016/j.enggeo.2014.08.008
  25. Armstrong-Hélouvry, B., Dupont, P., De Wit, C. C. (1994). A survey of models, analysis tools and compensation methods for the control of machines with friction. Automatica, 30 (7), 1083–1138. https://doi.org/10.1016/0005-1098(94)90209-7
  26. Luding, S., Clément, E., Blumen, A., Rajchenbach, J., Duran, J. (1994). Anomalous energy dissipation in molecular-dynamics simulations of grains: The «detachment» effect. Physical Review E, 50 (5), 4113–4122. https://doi.org/10.1103/physreve.50.4113
  27. Ketterhagen, W. R., Curtis, J. S., Wassgren, C. R. (2005). Stress results from two-dimensional granular shear flow simulations using various collision models. Physical Review E, 71 (6). https://doi.org/10.1103/physreve.71.061307
  28. Teufelsbauer, H., Wang, Y., Pudasaini, S. P., Borja, R. I., Wu, W. (2011). DEM simulation of impact force exerted by granular flow on rigid structures. Acta Geotechnica, 6 (3), 119–133. https://doi.org/10.1007/s11440-011-0140-9
  29. Mansouri, M., El Youssoufi, M. S., Nicot, F. (2016). Numerical simulation of the quicksand phenomenon by a 3D coupled Discrete Element – Lattice Boltzmann hydromechanical model. International Journal for Numerical and Analytical Methods in Geomechanics, 41 (3), 338–358. https://doi.org/10.1002/nag.2556
  30. Gallas, J. A. C., Herrmann, H. J., Sokołowski, S. (1992). Molecular dynamics simulation of powder fluidization in two dimensions. Physica A: Statistical Mechanics and Its Applications, 189 (3-4), 437–446. https://doi.org/10.1016/0378-4371(92)90055-u
  31. Melin, S. (1994). Wave propagation in granular assemblies. Physical Review E, 49 (3), 2353–2361. https://doi.org/10.1103/physreve.49.2353
  32. Wei, H., Li, M., Li, Y., Ge, Y., Saxén, H., Yu, Y. (2019). Discrete Element Method (DEM) and Experimental Studies of the Angle of Repose and Porosity Distribution of Pellet Pile. Processes, 7 (9), 561. https://doi.org/10.3390/pr7090561
  33. Wei, S., Wei, H., Saxen, H., Yu, Y. (2022). Numerical Analysis of the Relationship between Friction Coefficient and Repose Angle of Blast Furnace Raw Materials by Discrete Element Method. Materials, 15 (3), 903. https://doi.org/10.3390/ma15030903
  34. Dhaouadi, W., Marteau, E., Kolvenbach, H., Choukroun, M., Molaro, J. L., Hodyss, R., Schulson, E. M. (2021). Discrete element modeling of planetary ice analogs: mechanical behavior upon sintering. Granular Matter, 24 (1). https://doi.org/10.1007/s10035-021-01167-6
Development of the stick-slip friction model for discrete elements modeling

Downloads

Published

2024-08-26

How to Cite

Khellaf, A., & Mansouri, M. (2024). Development of the stick-slip friction model for discrete elements modeling. Technology Audit and Production Reserves, 4(1(78), 17–25. https://doi.org/10.15587/2706-5448.2024.310428

Issue

Vol. 4 No. 1(78) (2024): Industrial and technology systems

Section

Mechanics

License

Copyright (c) 2024 Abdelghani Khellaf, Mouloud Mansouri

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.