Розробка методології підтримки прийняття рішень для оптимізації ROI в управлінні проєктами
DOI:
https://doi.org/10.15587/2706-5448.2025.326385Ключові слова:
Fuzzy TOPSIS, оптимізація ROI, Fuzzy AHP, управління проєктами, аналіз рішеньАнотація
Об’єктом дослідження є процес прийняття рішень в управлінні проєктами з метою підвищення ефективності та оптимізації рентабельності інвестицій (ROI, з англ. Return on Investment). Однією з основних проблем, виявлених під час аудиту, є обмежена здатність традиційних методів багатокритеріального прийняття рішень (MCDM, з англ. Multi-Criteria Decision Making), таких як метод MOORA (Multi-Objective Optimization on the Basis of Ratio Analysis) та метод WASPAS (Weighted Aggregated Sum Product Assessment), ефективно функціонувати в умовах невизначеності, враховувати якісні експертні оцінки, забезпечувати об’єктивність обчислень та стабільність ранжування при зміні ваг критеріїв або появі нових альтернатив і зовнішніх чинників.
Для вирішення цих обмежень було застосовано інтегровану модель прийняття рішень на основі нечіткої логіки, яка об’єднує Fuzzy AHP (Fuzzy Analytic Hierarchy Process) та Fuzzy TOPSIS (Fuzzy Technique for Order Preference by Similarity to Ideal Solution). Метод Fuzzy AHP дозволив визначити ваги критеріїв на основі парних порівнянь експертів із використанням лінгвістичних формулювань, які перетворювалися в трикутні нечіткі числа. Метод Fuzzy TOPSIS забезпечив ранжування альтернатив відповідно до ступеня їх наближеності до ідеального рішення в умовах невизначеності.
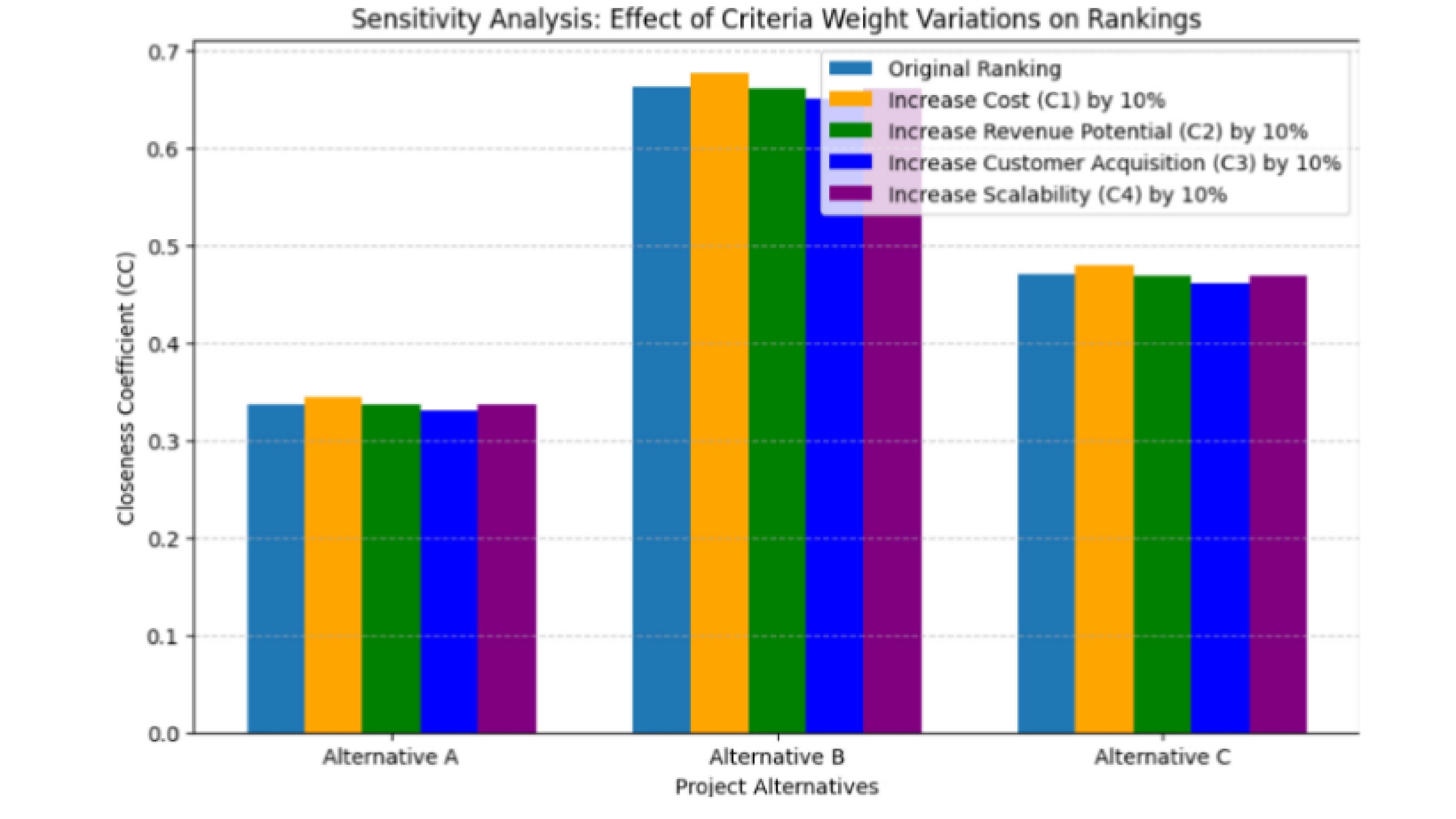
Методологія також включала аналіз чутливості та тест зворотного ранжування для перевірки стійкості та надійності моделі. У результаті було отримано стабільне ранжування трьох проєктних альтернатив, де Альтернатива B досягла найвищого коефіцієнта близькості (0.6628), що свідчить про її найвищу інвестиційну привабливість.
Запропонована модель інтегрує експертні знання, нечітку логіку та математичне моделювання, а також адаптується до змін, неповних даних і варіативності критеріїв. У порівнянні з класичними MCDM-підходами, вона демонструє підвищену точність, гнучкість, прозорість та стійкість у складних динамічних середовищах прийняття рішень.
Посилання
- Ibbs, C. W., Reginato, J. M., Kwak, Y. H. (2007). Developing project management capability: Benchmarking, maturity, modeling, gap analyses, and ROI studies. The Wiley Guide to Project Organization & Project Management Competencies, 270–289.
- Danesh, D., Ryan, M. J., Abbasi, A. (2018). Multi-criteria decision-making methods for project portfolio management: a literature review. International Journal of Management and Decision Making, 17 (1), 75–94. https://doi.org/10.1504/ijmdm.2018.088813
- Manurung, S., Simamora, I. M. S., Allagan, H. (2021). Comparison of Moora, Waspas, and SAW methods in decision support systems. Jurnal Mantik, 5 (2), 485–493.
- Jayant, A., Singh, S., Garg, S. K. (2018). An integrated approach with MOORA, SWARA, and WASPAS methods for selection of 3PLSP. Proceedings of the International Conference on Industrial Engineering and Operations Management, 2497–2509.
- Singh, R., Pathak, V. K., Kumar, R., Dikshit, M., Aherwar, A., Singh, V., Singh, T. (2024). A historical review and analysis on MOORA and its fuzzy extensions for different applications. Heliyon, 10 (3), e25453. https://doi.org/10.1016/j.heliyon.2024.e25453
- Miç, P., Antmen, Z. F. (2021). A Decision-Making Model Based on TOPSIS, WASPAS, and MULTIMOORA Methods for University Location Selection Problem. Sage Open, 11 (3). https://doi.org/10.1177/21582440211040115
- Pathapalli, V. R., Basam, V. R., Gudimetta, S. K., Koppula, M. R. (2019). Optimization of machining parameters using WASPAS and MOORA. World Journal of Engineering, 17 (2), 237–246. https://doi.org/10.1108/wje-07-2019-0202
- Mohagheghi, V., Mousavi, S. M. (2019). A new framework for high-technology project evaluation and project portfolio selection based on Pythagorean fuzzy WASPAS, MOORA, and mathematical modeling. Iranian Journal of Fuzzy Systems, 16 (6), 89–106.
- Talebi, K., Sartipi Pour, M., Azad, M., Ebrahim, H. (2024). A review of prioritization methods in preserving valuable villages. Journal of Rural Development.
- Chan, H. K., Sun, X., Chung, S.-H. (2019). When should fuzzy analytic hierarchy process be used instead of analytic hierarchy process? Decision Support Systems, 125, 113114. https://doi.org/10.1016/j.dss.2019.113114
- Sadiq, R., Tesfamariam, S. (2009). Environmental decision-making under uncertainty using intuitionistic fuzzy analytic hierarchy process (IF-AHP). Stochastic Environmental Research and Risk Assessment, 23 (4), 75–91. https://doi.org/10.1007/s00477-007-0197-z
- Hendrawan, A. (2024). The Comparative Analysis of Multi-Criteria Decision-Making Methods (MCDM) In Priorities of Industrial Location Development. Jurnal Infotel, 16 (4), 793–818. https://doi.org/10.20895/infotel.v16i4.1099
- Sultana, Mst. N., Sarker, O. S., Dhar, N. R. (2025). Parametric optimization and sensitivity analysis of the integrated Taguchi-CRITIC-EDAS method to enhance the surface quality and tensile test behavior of 3D printed PLA and ABS parts. Heliyon, 11 (1), e41289. https://doi.org/10.1016/j.heliyon.2024.e41289
- Kabir, G., Hasin, M. A. A. (2011). Comparative analysis of AHP and fuzzy AHP models for multi-criteria inventory classification. International Journal of Fuzzy Logic Systems, 3 (1), 21–36.
- Saad, S. M., Kunhu, N., Mohamed, A. M. (2016). A fuzzy-AHP multi-criteria decision-making model for procurement process. International Journal of Logistics Systems and Management, 23 (1). https://doi.org/10.1504/ijlsm.2016.073295
- Nieto-Morote, A., Ruz-Vila, F. (2011). A fuzzy ahp multi-criteria decision-making approach applied to combined cooling, heating, and power production systems. International Journal of Information Technology & Decision Making, 10 (3), 497–517. https://doi.org/10.1142/s0219622011004427
- Aladağ Mert, Y. (2023). Ranking of families applying for social aids using fuzzy AHP. ITU Library Repository.
- Kahraman, C., Onar, S. C., Cebi, S., Oztaysi, B., Tolga, A. C., Ucal Sari, I. (2024). Intelligent and Fuzzy Systems. Proceedings of the INFUS 2024 Conference. Springer. https://doi.org/10.1007/978-3-031-67195-1
- Liu, F., Peng, Y., Zhang, W., Pedrycz, W. (2017). On Consistency in AHP and Fuzzy AHP. Journal of Systems Science and Information, 5 (2), 128–147. https://doi.org/10.21078/jssi-2017-128-20
- Kou, G., Ergu, D., Lin, C., Chen, Y. (2016). Pairwise comparison matrix in multiple criteria decision making. Technological and economic development of economy, 22 (5), 738–765. https://doi.org/10.3846/20294913.2016.1210694
- Guo, S., Zhao, H. (2017). Fuzzy best-worst multi-criteria decision-making method and its applications. Knowledge-Based Systems, 121, 23–31. https://doi.org/10.1016/j.knosys.2017.01.010
- Gardashova, L. A. (2024). Decision-Making on the Information Technology Investment Problem Under Z-Environment. 16th International Conference on Applications of Fuzzy Systems, Soft Computing and Artificial Intelligence Tools – ICAFS-2023, 53–62. https://doi.org/10.1007/978-3-031-76283-3_10
- Siregar, V. M. M., Tampubolon, M. R., Parapat, E. P. S., Malau, E. I., Hutagalung, D. S. (2021). Decision support system for selection technique using MOORA method. IOP Conference Series: Materials Science and Engineering, 1088 (1), 012022. https://doi.org/10.1088/1757-899x/1088/1/012022
##submission.downloads##
Опубліковано
Як цитувати
Номер
Розділ
Ліцензія
Авторське право (c) 2025 Alish Nazarov

Ця робота ліцензується відповідно до Creative Commons Attribution 4.0 International License.
Закріплення та умови передачі авторських прав (ідентифікація авторства) здійснюється у Ліцензійному договорі. Зокрема, автори залишають за собою право на авторство свого рукопису та передають журналу право першої публікації цієї роботи на умовах ліцензії Creative Commons CC BY. При цьому вони мають право укладати самостійно додаткові угоди, що стосуються неексклюзивного поширення роботи у тому вигляді, в якому вона була опублікована цим журналом, але за умови збереження посилання на першу публікацію статті в цьому журналі.








