Обґрунтування параметрів активного конусного деформатора деревини
DOI:
https://doi.org/10.15587/2706-5448.2025.329722Ключові слова:
технологія, біомаса, деревина, активний деформатор, анізотропний матеріал, розколювання, зусилля руйнуванняАнотація
Об'єктом дослідження є параметри механізмів для руйнування анізотропних матеріалів механічним деформатором конусного виду. Одним із відомих відновлюваних джерел енергії є матеріал рослинного походження (деревина). Виходячи з цього пошук оптимальних параметрів роботи та конструктивних особливостей робочих органів для механізованого розколювання колод є актуальним. Тому запропоновано нове вирішення наукової задачі, що полягає в обґрунтуванні основних геометричних параметрів активного конусного деформатора для розколювання колод із деревини за найменшими енергетичними затратами на його привід.
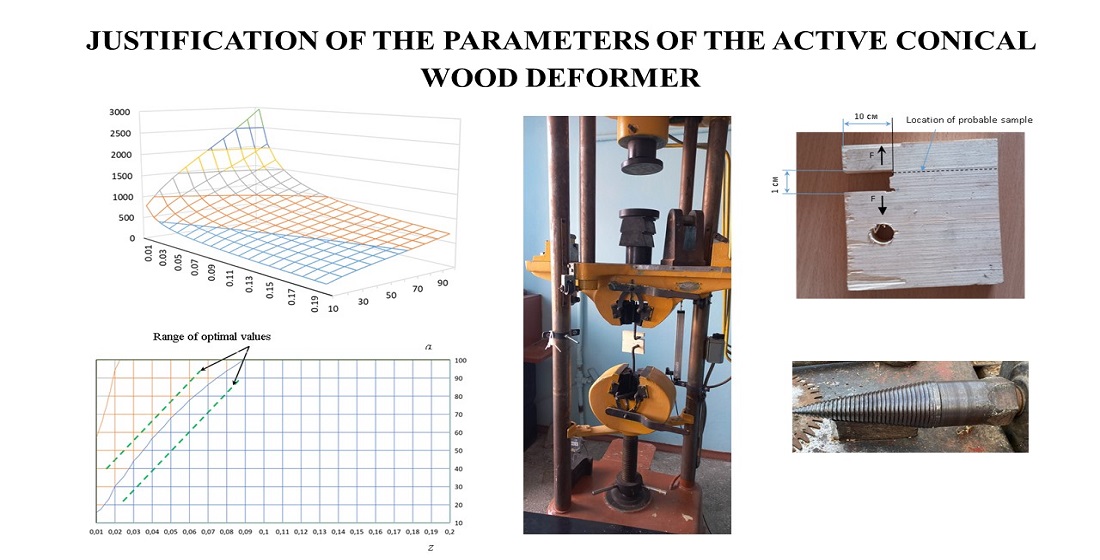
Проведений у ході дослідження аналіз показав загальну позитивну ознаку принципу роботи, при якій проникнення активного деформатора конусної форми перпендикулярно деревинним волокнам полегшує руйнування їх зав’язків та має більш перспективну та продуктивну конструкцію. Розроблено математичну модель визначення сили, що потрібна для руйнування колоди деревини. Зазначена залежність враховує пружні характеристики матеріалу, сили, що існують між волокнами анізотропної речовини, сили тертя між матеріалом деформатора та деревиною, та його геометричні параметри. Визначено, що необхідною величиною, котра характеризує фізико-механічні властивості деревини, є зусилля, яке необхідне для руйнування зв’язків між волокнами (коефіцієнт повздовжнього руйнування). Тому експериментально були отримані значення коефіцієнту повздовжнього руйнування, який склав для сосни – 2533 ± 66 H/м, дуба – 5583 ± 145 H/м та осики – 5000 ± 279 H/м.
За результатами досліджень отримані аналітичні рекомендації геометричних параметрів активного деформатора. Для матеріалу сосни діаметром 0,15 м оптимальна довжина конуса знаходиться в діапазоні 0,02–0,20 м при куті конуса – 20–90°. При цьому теоретичне зусилля на її руйнування складає 568–864 Н. Аналогічні результати отримані також для матеріалів осики та дуба. Завдяки цьому забезпечується можливість проєктувати конструкцію конусного деформатора деревини за зазначеними діапазонами, що є оптимальними для кожного матеріалу або їх груп.
Посилання
- Gorbenko, O., Lyashenko, S., Kelemesh, A., Padaka, V., Kalinichenko, A. (2021). Waste Usage as Secondary Resources. Procedia Environmental Science, Engineering and Management, 8 (2), 417–429. Available at: https://www.scopus.com/inward/record.uri?eid=2-s2.0-85101384718&partnerID=40&md5=0f37db7a2ed0b54f62c2d50be70d056e
- Gorb, O., Rębilas, R., Aranchiy, V., Yasnolob, I., Boiko, S., Padalka, V. (2020). Strengthening Competitiveness of the National Economy by Inhancing Energy Efficiency and Diversifying Energy Supply Sources in Rural Areas. Journal of Environmental Management and Tourism, 11 (5), 1114–1123. https://doi.org/10.14505//jemt.v11.5(45).09
- Kulyk, M. I., Padalka, V. V.; Illiashenko, N. S. (Ed.) (2020). Rozvytok bioenerhetyky na osnovi roslynnoho enerhetychnoho resursu (na prykladi Poltavskoi oblasti). Upravlinnia stratehiiamy vyperedzhaiuchoho innovatsiinoho rozvytku. Sumy: Trytoriia, 109–118.
- Özden, S., Slater, D., Ennos, R. (2017). Fracture properties of green wood formed within the forks of hazel (Corylus avellana L.). Trees, 31 (3), 903–917. https://doi.org/10.1007/s00468-016-1516-0
- Özden, S., Ennos, A. R., Cattaneo, M. E. G. V. (2016). Transverse fracture properties of green wood and the anatomy of six temperate tree species. Forestry, 90 (1), 58–69. https://doi.org/10.1093/forestry/cpw023
- Gurney, C., Hunt, J. (1967). Quasi-static crack propagation. Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences, 299 (1459), 508–524. https://doi.org/10.1098/rspa.1967.0152
- Ennos, A. R., van Casteren, A. (2009). Transverse stresses and modes of failure in tree branches and other beams. Proceedings of the Royal Society B: Biological Sciences, 277 (1685), 1253–1258. https://doi.org/10.1098/rspb.2009.2093
- Atkins, T. (2009). The Science and Engineering of Cutting: The Mechanics and Processes of Separating, Scratching and Puncturing Biomaterials, Metals and Non-Metals. Amsterdam: Elsevier, 432. https://doi.org/10.1016/c2009-0-17178-7
- Aicher, S., Reinhardt, H. W. (1993). Einfluß der Bauteilgröße in der linearen und nichtlinearen (Holz-)Bruchmechanik. Holz Als Roh- Und Werkstoff, 51 (3), 215–220. https://doi.org/10.1007/bf02628282
- Stanzl-Tschegg, S. E. (2006). Microstructure and fracture mechanical response of wood. International Journal of Fracture, 139 (3-4), 495–508. https://doi.org/10.1007/s10704-006-0052-0
- Tschegg, E. K., Humer, K., Weber, H. W. (1993). Fracture tests in Mode I on fibre-reinforced plastics. Journal of Materials Science, 28 (9), 2471–2480. https://doi.org/10.1007/bf01151682
- Shukla, S. R.; Mandal, A. K., Nicodemus, A. (Eds.) (2025). Wood Properties and Utilization. Textbook of Forest Science, 811–838. https://doi.org/10.1007/978-981-97-8289-5_37
- Pinto Moreira, A., da Silveira, E., Henrique de Almeida, D., Hendrigo de Almeida, T. et al. (2017). Toughness and Impact Strength in Dynamic Bending of Wood as a Function of the Modulus of Elasticity and the Strength in Compression to the Grain. International Journal of Materials Engineering, 7 (4), 61–67. https://doi.org/10.5923/j.ijme.20170704.01
- Stanzl-Tschegg, S. E., Tan, D.-M., Tschegg, E. (1995). New splitting method for wood fracture characterization. Wood Science and Technology, 29 (1), 31–50. https://doi.org/10.1007/bf00196930
- Kollmann, F. F. P. (1968). Mechanics and Rheology of Wood. Principles of Wood Science and Technology. Springer, Berlin, Heidelberg, 292–419. https://doi.org/10.1007/978-3-642-87928-9_7
- Padalka, V., Liashenko, S., Kalinichenko, A., Burlaka, O., Sakalo, V., Padalka, Y. (2021). Modeling of Resonance Phenomena in Self-Oscillating System of Agricultural Machines. 2021 IEEE International Conference on Modern Electrical and Energy Systems (MEES), 1–6. https://doi.org/10.1109/mees52427.2021.9598763
- Piatak, M. H., Padalka, V. V. (2024). Study of physical and mechanical properties of plant fruits on the example of walnut. Scientific Progress & Innovations, 27 (2), 148–153. https://doi.org/10.31210/spi2024.27.02.26
- Babytskyi, L. F., Padalka, V. V., Liashenko, S. V. (2011). The research of laboratore investigation of working torsionno – udarnyy rykhlitel pochvy. Visnyk Kharkivskoho natsionalnoho tekhnichnoho universytetu silskoho hospodarstva. Mekhanizatsiia silskohospodarskoho vyrobnytstva, 1 (7), 284–291. Available at: https://repo.btu.kharkov.ua//handle/123456789/55894
- Ennos, A. R., Oliveira, J. A. V. (2017). The Mechanics of Splitting Wood and the Design of Neolithic Woodworking Tools. EXARC Journal, 2017/4. Available at: https://exarc.net/ark:/88735/10312
- Mikhailova, T., Mustafina, S., Mikhailov, V. (2021). Automation of data processing of the results of the chemical experiment on modeling the production of synthetic rubber using Microsoft Excel. Journal of Physics: Conference Series, 2092 (1), 012003. https://doi.org/10.1088/1742-6596/2092/1/012003
##submission.downloads##
Опубліковано
Як цитувати
Номер
Розділ
Ліцензія
Авторське право (c) 2025 Viacheslav Padalka, Oleksandr Gorbenko, Olena Ivankova, Volodymyr Dudnyk, Bohdan Horiunov

Ця робота ліцензується відповідно до Creative Commons Attribution 4.0 International License.
Закріплення та умови передачі авторських прав (ідентифікація авторства) здійснюється у Ліцензійному договорі. Зокрема, автори залишають за собою право на авторство свого рукопису та передають журналу право першої публікації цієї роботи на умовах ліцензії Creative Commons CC BY. При цьому вони мають право укладати самостійно додаткові угоди, що стосуються неексклюзивного поширення роботи у тому вигляді, в якому вона була опублікована цим журналом, але за умови збереження посилання на першу публікацію статті в цьому журналі.








