Analysis of methods and algorithms for quadrotor position control
DOI:
https://doi.org/10.15587/2706-5448.2025.333833Keywords:
quadrotor control, parametric and structural uncertainty, energy-based control, nonlinear MIMO systemsAbstract
The object of research is the system of position control of a quadrotor unmanned aerial vehicle (UAV) as a nonlinear multi-input multi-output (MIMO) system with strong cross-channel coupling and high sensitivity to parametric and structural uncertainty. The problem addressed is the lack of robust and computationally efficient control algorithms that can ensure stability under uncertainty and be implemented on embedded platforms with limited resources.
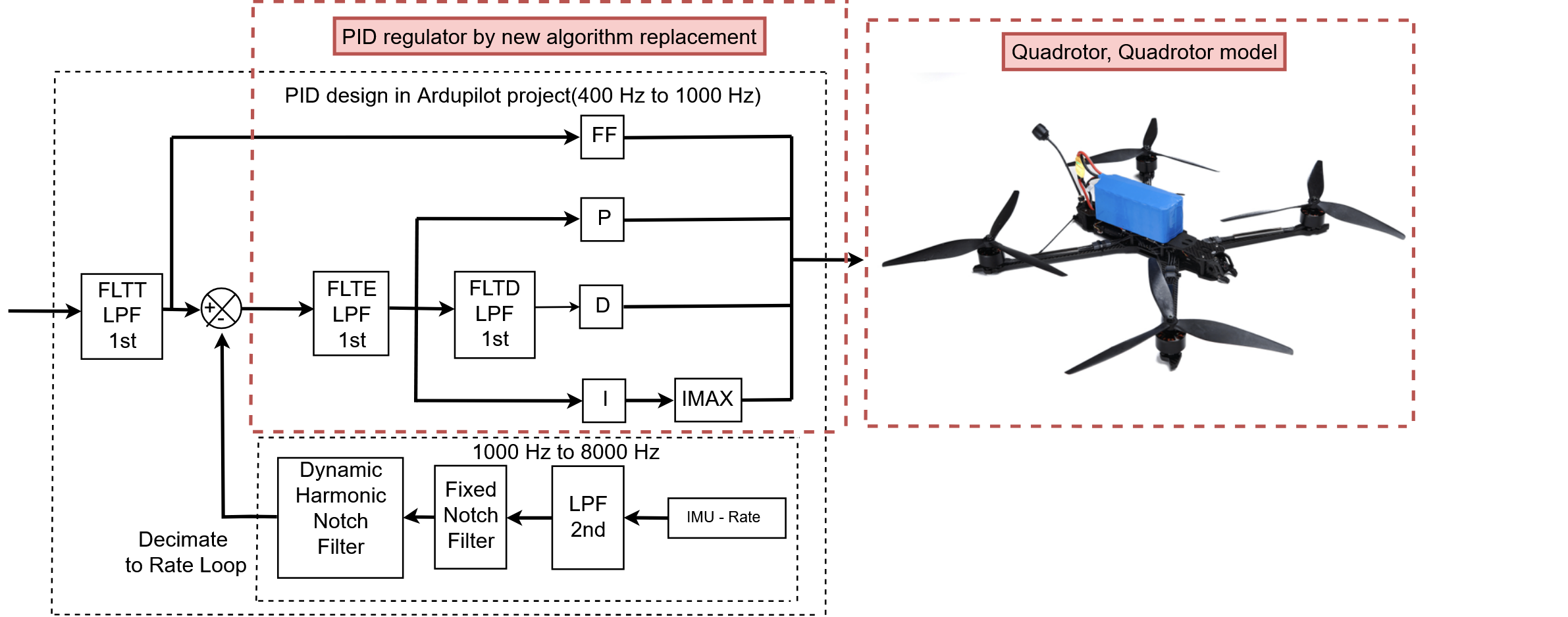
This study presents an analytical review of modern control methods for quadrotor position stabilization. The methods analyzed include classical proportional-integral-derivative (PID) controllers, linear optimal, robust, adaptive, and intelligent systems (neural networks, fuzzy logic). The analysis focuses on the structure, sensitivity to uncertainty, computational complexity, and feasibility of implementation on STM32-based flight controllers.
As a result of the review, it was established that classical PID controllers, while widely used, are highly sensitive to model variations and sensor noise. Intelligent systems show better adaptability but exceed the computational capacity of low-cost microcontrollers. The most promising direction is identified as energy-based control methods that minimize local functionals of instantaneous energy values. These methods allow generating closed-form control laws, avoid signal differentiation, and maintain robustness with minimal processor load.
The comparative evaluation shows that the proposed algorithm has the potential to improve control quality by more than 7% and reduce the impact of parametric disturbances by an average of 10% compared to traditional PID-based systems. The results are recommended for UAV control systems operating under limited computational capacity, absence of GPS, or in disturbed environments, such as tactical drones, FPV platforms, and autonomous navigation systems.
References
- Besnard, L., Shtessel, Y. B., Landrum, B. (2007). Control of a Quadrotor Vehicle Using Sliding Mode Disturbance Observer. 2007 American Control Conference. New York: IEEE, 5230–5235. https://doi.org/10.1109/acc.2007.4282421
- Dierks, T., Jagannathan, S. (2010). Output Feedback Control of a Quadrotor UAV Using Neural Networks. IEEE Transactions on Neural Networks, 21 (1), 50–66. https://doi.org/10.1109/tnn.2009.2034145
- Hedjar, R., Al Zuair, M. A. (2019). Robust Altitude Stabilization of VTOL-UAV for Payloads Delivery. IEEE Access, 7, 73583–73592. https://doi.org/10.1109/access.2019.2919701
- Barrón-Gómez, R. A., Ramos-Velasco, L. E., Espinoza Quesada, E. S., García Carrillo, L. R. (2017). Wavelet neural network PID controller for a UAS transporting a cable-suspended load. IFAC-PapersOnLine, 50 (1), 2335–2340. https://doi.org/10.1016/j.ifacol.2017.08.419
- Kayacan, E., Maslim, R. (2017). Type-2 Fuzzy Logic Trajectory Tracking Control of Quadrotor VTOL Aircraft with Elliptic Membership Functions. IEEE/ASME Transactions on Mechatronics, 22 (1), 339–348. https://doi.org/10.1109/tmech.2016.2614672
- Wang, H., Xiaoping Liu, P., Xie, X., Liu, X., Hayat, T., Alsaadi, F. E. (2021). Adaptive fuzzy asymptotical tracking control of nonlinear systems with unmodeled dynamics and quantized actuator. Information Sciences, 575, 779–792. https://doi.org/10.1016/j.ins.2018.04.011
- Li, S., Wang, Y., Tan, J., Zheng, Y. (2016). Adaptive RBFNNs/integral sliding mode control for a quadrotor aircraft. Neurocomputing, 216, 126–134. https://doi.org/10.1016/j.neucom.2016.07.033
- Lee, T. (2013). Robust Adaptive Attitude Tracking on SO (3) With an Application to a Quadrotor UAV. IEEE Transactions on Control Systems Technology, 21 (5), 1924–1930. https://doi.org/10.1109/tcst.2012.2209887
- Hedjar, R. (2015). Robust one-step-ahead model predictive control of VTOL-UAVs. The 27th Chinese Control and Decision Conference (2015 CCDC). Qingdao: IEEE, 3053–3058. https://doi.org/10.1109/ccdc.2015.7162445
- Ostroverkhov, M., Pyzhov, V., Korol, S. (2017). Control of the electric drive under conditions of parametric uncertainty and coordinates’ interrelation. 2017 International Conference on Modern Electrical and Energy Systems (MEES). Kremenchuk: IEEE, 64–67. https://doi.org/10.1109/mees.2017.8248953
- Ostroverkhov, M., Pyzhov, V. (2019). Control of the Electric Drive with Field Regulated Reluctance Machine. 2019 IEEE 6th International Conference on Energy Smart Systems (ESS). Kyiv: IEEE, 277–282. https://doi.org/10.1109/ess.2019.8764206
- ArduPilot. Available at: https://ardupilot.org/
- Copter Attitude Control. ArduPilot. Available at: https://ardupilot.org/dev/docs/apmcopter-programming-attitude-control-2.html
- Satskyi, I. S., Ostroverkhov, М. Ya. (2025). Improving the quality of unmanned aerial vehicle attitude control under conditions of parametric and structural uncertainty. Development priorities for technical sciences in the modern world. Riga, 54–57. https://doi.org/10.30525/978-9934-26-542-6-14
Downloads
Published
How to Cite
Issue
Section
License
Copyright (c) 2025 Mykola Ostroverkhov, Illia Satskyi

This work is licensed under a Creative Commons Attribution 4.0 International License.
The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.







