Time history nonlinear analysis for 2D modelization of an existing building using flexibility and displacement-based formulation
DOI:
https://doi.org/10.15587/2706-5448.2024.298870Keywords:
flexibility-based, displacement-based, time-history analysis, frame structures, nonlinear analyses, Euler-Bernoulli frame elementAbstract
The object of the research is the response of a structure in time between formulations, namely force-based (flexibility-based) and displacement-based.
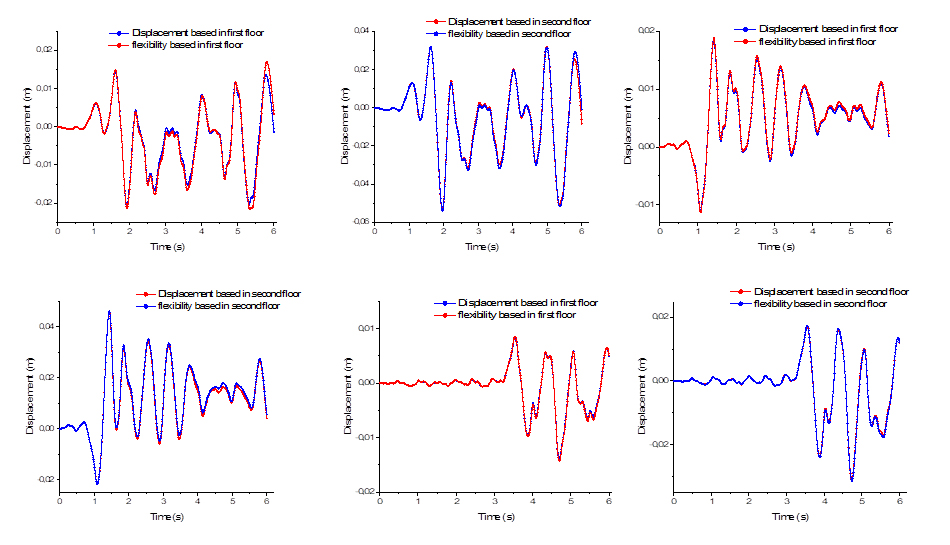
An existing two-story reinforced concrete structure subjected to three earthquakes separately is presented in order to carry out a comparative study in terms of time history structure response between the two formulations cited above namely force based (flexibility based) and displacement based.
This research aimed to compare between two formulations namely displacement based and force-based (flexibility-based), in order to show the accuracy and the reliability of the second one. In the case of nonlinear time history response of a residential two-storey reinforced concrete building, which is representative of typical residential building construction in Italy in the 1970’s and 1980’s with the aim of taking advantages of flexibility-based formulation if the comparison proves conclusive.
In the course of the research, the former approach is a classical two-node, displacement-based, Euler-Bernoulli frame element with the disadvantage of discretizing the structure thus increasing the number of degrees of freedom and equation, in order to achieve the required precision. The latter is a two-node, force-based, Euler Bernoulli frame element. The main advantage of the second element is that it is «exact» within the relevant frame element theory. This implies that one element per frame member (beam or column) is used in preparing the frame mesh, thus leading to a reduction of the global number of degrees of freedom. Therefore, a reduction in number of equations to solve, resulting in a saving of time with increased precision.
An existing two-story reinforced concrete structure subjected to three earthquakes separately is presented in order to carry out a comparative study in terms of time history structure response between the two formulations cited above namely force based (flexibility-based) and displacement-based. As a result of the research, it is shown that with flexibility-based approach no discretization error occurs and all governing equations are satisfied exactly, making a possibility of simpler and faster numerical modeling. In the proposed approach will be of great use in the field of numerical modeling due to its ease and accuracy. This elegant formulation is promising for future work thanks to its advantages.
References
- Belgasmia, M. (2021) Structural dynamics and static nonlinear analysis from theory to application. Engineering Science Reference, an imprint of IGI Global. Hershey.
- Walport, F., Arrayago, I., Gardner, L., Nethercot, D. A. (2021). Influence of geometric and material nonlinearities on the behaviour and design of stainless steel frames. Journal of Constructional Steel Research, 187, 106981. doi: https://doi.org/10.1016/j.jcsr.2021.106981
- Alemdar, B. N., White, D. W. (2005). Displacement, Flexibility, and Mixed Beam–Column Finite Element Formulations for Distributed Plasticity Analysis. Journal of Structural Engineering, 131 (12), 1811–1819. doi: https://doi.org/10.1061/(asce)0733-9445(2005)131:12(1811)
- Hjelmstad, K. D., Taciroglu, E. (2005). Variational Basis of Nonlinear Flexibility Methods for Structural Analysis of Frames. Journal of Engineering Mechanics, 131 (11), 1157–1169. doi: https://doi.org/10.1061/(asce)0733-9399(2005)131:11(1157)
- Spacone, E., Filippou, F. C., Taucer, F. F. (1996). Fiber beamcolumn model for nonlinear analysis of R/C frames. I: Formulation, II: Applications. Earthquake Engineering & Structural Dynamics, 25 (7), 727–742. doi: https://doi.org/10.1002/(sici)1096-9845(199607)25:7<727::aid-eqe577>3.3.co;2-f
- Neuenhofer, A., Filippou, F. C. (1998). Geometrically Nonlinear Flexibility-Based Frame Finite Element. Journal of Structural Engineering, 124 (6), 704–711. doi: https://doi.org/10.1061/(asce)0733-9445(1998)124:6(704)
- Reynders, E., De Roeck, G. (2010). A local flexibility method for vibration-based damage localization and quantification. Journal of Sound and Vibration, 329 (12), 2367–2383. doi: https://doi.org/10.1016/j.jsv.2009.04.026
- Mourad, B., Sabah, M. (2015). Comparison between static nonlinear and time history analysis using flexibility-based model for an existing structure and effect of taking into account soil using Domain Reduction Method for a single media. KSCE Journal of Civil Engineering, 19 (3), 651–663. doi: https://doi.org/10.1007/s12205-015-0351-y
- Hjelmstad, K. D., Taciroglu, E. (2002). Mixed methods and flexibility approaches for nonlinear frame analysis. Journal of Constructional Steel Research, 58 (5-8), 967–993. doi: https://doi.org/10.1016/s0143-974x(01)00100-6
- Valipour, H. R., Foster, S. J. (2010). A total secant flexibility-based formulation for frame elements with physical and geometrical nonlinearities. Finite Elements in Analysis and Design, 46 (3), 288–297. doi: https://doi.org/10.1016/j.finel.2009.11.002
- Güney, D., Kurusçu, A. O. (2011). Optimization of the configuration of infill walls in order to increase seismic resistance of building structures. International Journal of the Physical Sciences, 6 (4), 698–706.
Downloads
Published
How to Cite
Issue
Section
License
Copyright (c) 2024 Mourad Belgasmia, Sabah Moussaoui, Rebadj Chabane

This work is licensed under a Creative Commons Attribution 4.0 International License.
The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.







