Розгляд електронного середнього транспорту тепла через систему низького розміру
DOI:
https://doi.org/10.15587/2706-5448.2024.300260Ключові слова:
теорія відповідності фазового поля (PMFT), жорстке прив'язування (TB), формалізм Ландауера Бюттікера, функції ГрінаАнотація
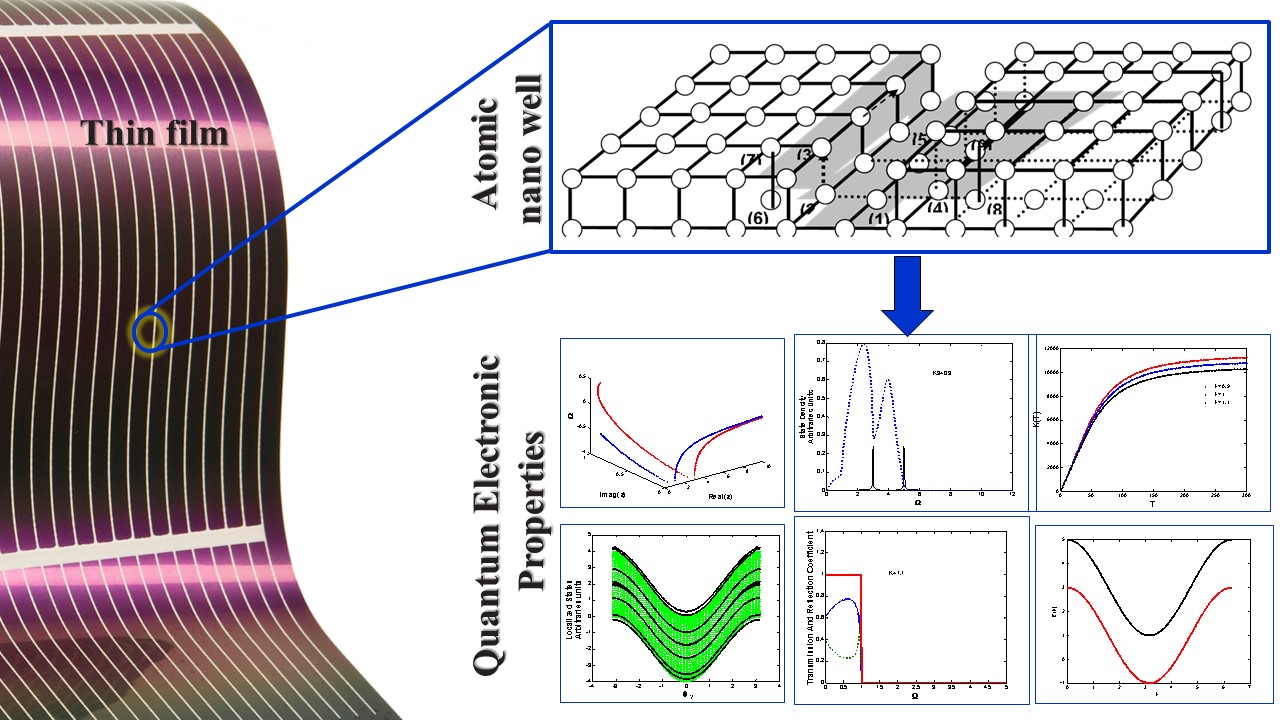
Об’єктом дослідження є складна сфера локалізації енергії та когерентного балістичного електронного транспорту в низькорозмірних кремнієвих квантових дротах, зокрема тих, що леговані атомами германію. На відміну від своїх тривимірних аналогів, низьковимірні системи демонструють унікальну поведінку електронного транспорту, що вимагає нових аналітичних підходів для всебічного розуміння. Як ядро це дослідження використовує теорію узгодження фазового поля (PMFT) і наближення жорсткого зв’язку (TB), складні методології, які дозволяють глибоко зануритися в квантово-механічні нюанси цих систем. Через цю лінзу досліджено складну динаміку дисперсійних співвідношень, фазових факторів, групових швидкостей та, зокрема, вплив дефектів, утворених легуванням германієм.
Це дослідження ретельно аналізує, як ці дефекти впливають на електронну та теплопровідність, а також на щільність станів, пропонуючи нове розуміння ролі резонансів Фано у флуктуаціях спектрів пропускання та відбиття. Виявлено, що ці резонанси в значній мірі залежать від природи дефектів, їх конфігурації та електронних параметрів поблизу них, підкреслюючи нюанси взаємодії між складом матеріалу та електронними властивостями в системах низької розмірності.
Наслідки зроблених висновків виходять далеко за рамки теоретичних. Вони прокладають шлях для значних досягнень у нанотехнологіях і дизайні електронних пристроїв, підкреслюючи потенціал для створення більш ефективних, високопродуктивних компонентів. Крім того, ця робота пропонує структуру для розробки методологій неруйнівного контролю, які могли б зробити революцію в матеріалознавстві, забезпечивши точний аналіз дефектів у системах низької розмірності, не завдаючи шкоди. Це особливо важливо для поточної розробки матеріалів з оптимізованими властивостями для різних застосувань, від електроніки до зберігання енергії.
По суті, це дослідження не тільки збагачує наше розуміння фізики, яка керує системами низької розмірності, але також пропонує практичне розуміння того, як використовувати ці властивості для технологічних інновацій. Подолаючи розрив між теоретичною фізикою та матеріалознавством, це дослідження закладає основу для наступного покоління електронних компонентів і методів неруйнівного оцінювання, знаменуючи значний крок вперед у застосуванні квантової механіки до реальних проблем.
Посилання
- Neuhaus, D.-H., Münzer, A. (2007). Industrial Silicon Wafer Solar Cells. Advances in OptoElectronics, 2007, 1–15. doi: https://doi.org/10.1155/2007/24521
- Fuechsle, M., Miwa, J. A., Mahapatra, S., Ryu, H., Lee, S., Warschkow, O. et al. (2012). A single-atom transistor. Nature Nanotechnology, 7 (4), 242–246. doi: https://doi.org/10.1038/nnano.2012.21
- Ferrari, A. C., Bonaccorso, F., Fal'Ko, V., Novoselov, K. S., Roche, S., Bøggild, P. et al. (2015). Science and technology roadmap for graphene, related two-dimensional crystals, and hybrid systems. Nanoscale, 7 (11), 4598–4810.
- Waldrop, M. M. (2016). The chips are down for Moore’s law. Nature, 530 (7589), 144–147. doi: https://doi.org/10.1038/530144a
- Luo, T., Chen, G. (2013). Nanoscale heat transfer – from computation to experiment. Physical Chemistry Chemical Physics, 15 (10), 3389. doi: https://doi.org/10.1039/c2cp43771f
- Luisier, M. (2014). Atomistic simulation of transport phenomena in nanoelectronic devices. Chemical Society Reviews, 43 (13), 4357–4367. doi: https://doi.org/10.1039/c4cs00084f
- Agraıt, N., Yeyati, A. L., Van Ruitenbeek, J. M. (2003). Quantum properties of atomic-sized conductors. Physics Reports, 377 (2-3), 81–279. doi: https://doi.org/10.1016/s0370-1573(02)00633-6
- Sørensen, H. H. B., Hansen, P. C., Petersen, D. E., Skelboe, S., Stokbro, K. (2009). Efficient wave-function matching approach for quantum transport calculations. Physical Review B, 79 (20). doi: https://doi.org/10.1103/physrevb.79.205322
- Nitzan, A., Ratner, M. A. (2003). Electron Transport in Molecular Wire Junctions. Science, 300 (5624), 1384–1389. doi: https://doi.org/10.1126/science.1081572
- Ke, Y., Xia, K., Guo, H. (2008). Disorder Scattering in Magnetic Tunnel Junctions: Theory of Nonequilibrium Vertex Correction. Physical Review Letters, 100 (16). doi: https://doi.org/10.1103/physrevlett.100.166805
- Markussen, T., Rurali, R., Jauho, A.-P., Brandbyge, M. (2007). Scaling Theory Put into Practice: First-Principles Modeling of Transport in Doped Silicon Nanowires. Physical Review Letters, 99 (7). doi: https://doi.org/10.1103/physrevlett.99.076803
- Nozaki, D., Pastawski, H. M., Cuniberti, G. (2010). Controlling the conductance of molecular wires by defect engineering. New Journal of Physics, 12 (6), 063004. doi: https://doi.org/10.1088/1367-2630/12/6/063004
- Khater, A., Szczęśniak, D. (2011). A simple analytical model for electronic conductance in a one dimensional atomic chain across a defect. Journal of Physics: Conference Series, 289, 012013. doi: https://doi.org/10.1088/1742-6596/289/1/012013
- Szczęśniak, D., Khater, A. (2012). Electronic conductance via atomic wires: a phase field matching theory approach. The European Physical Journal B, 85 (6). doi: https://doi.org/10.1140/epjb/e2012-21055-x
- Belayadi, A., Bourahla, B., Mekideche-Chafa, F. (2018). Localized electronic surface states in metallic structureS. Surface Review and Letters, 25 (5), 1850101. doi: https://doi.org/10.1142/s0218625x18501019
- Büttiker, M. (1986). Four-Terminal Phase-Coherent Conductance. Physical Review Letters, 57 (14), 1761–1764. doi: https://doi.org/10.1103/physrevlett.57.1761
- Landauer, R. (1957). Spatial Variation of Currents and Fields Due to Localized Scatterers in Metallic Conduction. IBM Journal of Research and Development, 1 (3), 223–231. doi: https://doi.org/10.1147/rd.13.0223
- Khomyakov, P. A., Brocks, G., Karpan, V., Zwierzycki, M., Kelly, P. J. (2005). Conductance calculations for quantum wires and interfaces: Mode matching and Green’s functions. Physical Review B, 72 (3). doi: https://doi.org/10.1103/physrevb.72.035450
- Mardaani, M., Rabani, H., Esmaeili, A. (2011). An analytical study on electronic density of states and conductance of typical nanowires. Solid State Communications, 151 (13), 928–932. doi: https://doi.org/10.1016/j.ssc.2011.04.010
- Rabani, H., Mardaani, M. (2012). Exact analytical results on electronic transport of conjugated polymer junctions: Renormalization method. Solid State Communications, 152 (3), 235–239. doi: https://doi.org/10.1016/j.ssc.2011.09.026
- Wu, Y., Childs, P. (2010). Conductance of Graphene Nanoribbon Junctions and the Tight Binding Model. Nanoscale Research Letters, 6 (1). doi: https://doi.org/10.1007/s11671-010-9791-y
- Slater, J. C., Koster, G. F. (1954). Simplified LCAO Method for the Periodic Potential Problem. Physical Review, 94 (6), 1498–1524. doi: https://doi.org/10.1103/physrev.94.1498
- Harrison, W. A. (2004). Elementary electronic structure (revised edition). World Scientific Publishing Company. doi: https://doi.org/10.1142/5432
- Wills, J. M., Harrison, W. A. (1984). Further studies on interionic interactions in simple metals and transition metals. Physical Review B, 29 (10), 5486–5490. doi: https://doi.org/10.1103/physrevb.29.5486
- Landauer, R. (1957). Spatial Variation of Currents and Fields Due to Localized Scatterers in Metallic Conduction. IBM Journal of Research and Development, 1 (3), 223–231. doi: https://doi.org/10.1147/rd.13.0223
- Belayadi, A., Bourahla, B. (2018). A theoretical model to compute the localized electronic states at the surface of hexagonal structures with different coupling orbitals. Surface Science, 675, 1–14. doi: https://doi.org/10.1016/j.susc.2018.04.005
- Bourahla, B., Nafa, O. (2016). Magnons Heat Transfer and Magnons Scattering in Magnetic Sandwich Lattices: Application to Fe/Gd(5)/Fe System. SPIN, 6 (3), 1650007. doi: https://doi.org/10.1142/s2010324716500077
- Bloch, F. (1929). Über die quantenmechanik der elektronen in kristallgittern. Zeitschrift für physik, 52 (7-8), 555–600. doi: https://doi.org/10.1007/bf01339455
- Feuchtwang, T. E. (1967). Dynamics of a Semi-Infinite Crystal Lattice in a Quasiharmonic Approximation. II. The Normal-Mode Analysis of a Semi-Infinite Lattice. Physical Review, 155 (3), 731–744. doi: https://doi.org/10.1103/physrev.155.731
- Szeftel, J., Khater, A. (1987). Calculation of surface phonons and resonances: the matching procedure revisited: I. Journal of Physics C: Solid State Physics, 20 (29), 4725–4736. doi: https://doi.org/10.1088/0022-3719/20/29/010
- Szczȩśniak, D., Khater, A., Ba̧k, Z., Szczȩśniak, R., Ghantous, M. A. (2012). Quantum conductance of silicon-doped carbon wire nanojunctions. Nanoscale Research Letters, 7 (1). doi: https://doi.org/10.1186/1556-276x-7-616
- Khater, A., Belhadi, M., Abou Ghantous, M. (2011). Phonons heat transport at an atomic well boundary in ultrathin solid films. The European Physical Journal B, 80 (3), 363–369. doi: https://doi.org/10.1140/epjb/e2011-10892-8
- Khater, A., Bourahla, B., Abou Ghantous, M., Tigrine, R., Chadli, R. (2011). Magnons coherent transmission and heat transport at ultrathin insulating ferromagnetic nanojunctions. The European Physical Journal B, 82 (1), 53–61. doi: https://doi.org/10.1140/epjb/e2011-10935-2
- Grimech, H., Khater, A. (1995). Calculation of the spectral densities of the surface alloy system (PtcCu1 – c1/Cu(100). Surface Science, 323 (3), 198–206. doi: https://doi.org/10.1016/0039-6028(94)00630-x
- Economou, E. N. (2006). Green's functions in quantum physics. Vol. 7. Springer Science & Business Media. doi: https://doi.org/10.1007/3-540-28841-4
- Pastawski, H. M., Medina, E. (2001). Tight Binding'methods in quantum transport through molecules and small devices: From the coherent to the decoherent description. doi: https://doi.org/10.48550/arXiv.cond-mat/0103219
##submission.downloads##
Опубліковано
Як цитувати
Номер
Розділ
Ліцензія
Авторське право (c) 2024 Zouaneb Aicha, Elfahem Sakher, Tigrine Rachid, Bendoura Abdallah, Aissa Benselhoub

Ця робота ліцензується відповідно до Creative Commons Attribution 4.0 International License.
Закріплення та умови передачі авторських прав (ідентифікація авторства) здійснюється у Ліцензійному договорі. Зокрема, автори залишають за собою право на авторство свого рукопису та передають журналу право першої публікації цієї роботи на умовах ліцензії Creative Commons CC BY. При цьому вони мають право укладати самостійно додаткові угоди, що стосуються неексклюзивного поширення роботи у тому вигляді, в якому вона була опублікована цим журналом, але за умови збереження посилання на першу публікацію статті в цьому журналі.








