Розгляд електронного середнього транспорту тепла через систему низького розміру

Автор(и)

DOI:

https://doi.org/10.15587/2706-5448.2024.300260

Ключові слова:

теорія відповідності фазового поля (PMFT), жорстке прив'язування (TB), формалізм Ландауера Бюттікера, функції Гріна

Анотація

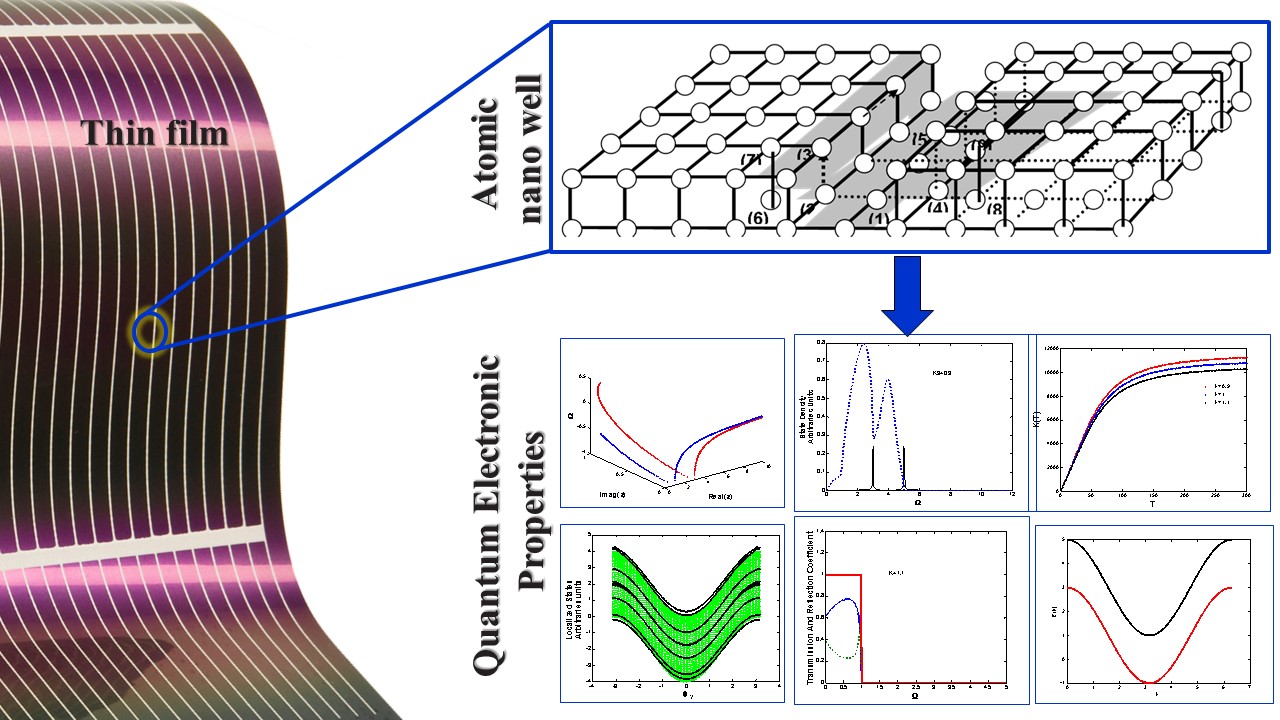
Об’єктом дослідження є складна сфера локалізації енергії та когерентного балістичного електронного транспорту в низькорозмірних кремнієвих квантових дротах, зокрема тих, що леговані атомами германію. На відміну від своїх тривимірних аналогів, низьковимірні системи демонструють унікальну поведінку електронного транспорту, що вимагає нових аналітичних підходів для всебічного розуміння. Як ядро це дослідження використовує теорію узгодження фазового поля (PMFT) і наближення жорсткого зв’язку (TB), складні методології, які дозволяють глибоко зануритися в квантово-механічні нюанси цих систем. Через цю лінзу досліджено складну динаміку дисперсійних співвідношень, фазових факторів, групових швидкостей та, зокрема, вплив дефектів, утворених легуванням германієм.

Це дослідження ретельно аналізує, як ці дефекти впливають на електронну та теплопровідність, а також на щільність станів, пропонуючи нове розуміння ролі резонансів Фано у флуктуаціях спектрів пропускання та відбиття. Виявлено, що ці резонанси в значній мірі залежать від природи дефектів, їх конфігурації та електронних параметрів поблизу них, підкреслюючи нюанси взаємодії між складом матеріалу та електронними властивостями в системах низької розмірності.

Наслідки зроблених висновків виходять далеко за рамки теоретичних. Вони прокладають шлях для значних досягнень у нанотехнологіях і дизайні електронних пристроїв, підкреслюючи потенціал для створення більш ефективних, високопродуктивних компонентів. Крім того, ця робота пропонує структуру для розробки методологій неруйнівного контролю, які могли б зробити революцію в матеріалознавстві, забезпечивши точний аналіз дефектів у системах низької розмірності, не завдаючи шкоди. Це особливо важливо для поточної розробки матеріалів з оптимізованими властивостями для різних застосувань, від електроніки до зберігання енергії.

По суті, це дослідження не тільки збагачує наше розуміння фізики, яка керує системами низької розмірності, але також пропонує практичне розуміння того, як використовувати ці властивості для технологічних інновацій. Подолаючи розрив між теоретичною фізикою та матеріалознавством, це дослідження закладає основу для наступного покоління електронних компонентів і методів неруйнівного оцінювання, знаменуючи значний крок вперед у застосуванні квантової механіки до реальних проблем.

Біографії авторів

Zouaneb Aicha, African University Ahmed Draia

Postgraduate Student

Laboratory of Energy Environment and Information System (LEEIS)

Department of Material Science, Faculty of Science and Technology

Elfahem Sakher, African University Ahmed Draia; Environmental Research Center (C.R.E) sis at Alzone

PhD, Lecturer

Laboratory of Energy Environment and Information System (LEEIS)

Department of Material Science, Faculty of Science and Technology

Associate Researcher

Tigrine Rachid, African University Ahmed Draia

Professor

Laboratory of Energy Environment and Information System (LEEIS)

Department of Material Science, Faculty of Science and Technology

Bendoura Abdallah, African University Ahmed Draia

Postgraduate Student

Laboratory of Energy Environment and Information System (LEEIS)

Department of Material Science, Faculty of Science and Technology

Aissa Benselhoub, Environmental Research Center (C.R.E)

Associate Researcher

Environment, Modeling and Climate Change Division

Посилання

  1. Neuhaus, D.-H., Münzer, A. (2007). Industrial Silicon Wafer Solar Cells. Advances in OptoElectronics, 2007, 1–15. doi: https://doi.org/10.1155/2007/24521
  2. Fuechsle, M., Miwa, J. A., Mahapatra, S., Ryu, H., Lee, S., Warschkow, O. et al. (2012). A single-atom transistor. Nature Nanotechnology, 7 (4), 242–246. doi: https://doi.org/10.1038/nnano.2012.21
  3. Ferrari, A. C., Bonaccorso, F., Fal'Ko, V., Novoselov, K. S., Roche, S., Bøggild, P. et al. (2015). Science and technology roadmap for graphene, related two-dimensional crystals, and hybrid systems. Nanoscale, 7 (11), 4598–4810.
  4. Waldrop, M. M. (2016). The chips are down for Moore’s law. Nature, 530 (7589), 144–147. doi: https://doi.org/10.1038/530144a
  5. Luo, T., Chen, G. (2013). Nanoscale heat transfer – from computation to experiment. Physical Chemistry Chemical Physics, 15 (10), 3389. doi: https://doi.org/10.1039/c2cp43771f
  6. Luisier, M. (2014). Atomistic simulation of transport phenomena in nanoelectronic devices. Chemical Society Reviews, 43 (13), 4357–4367. doi: https://doi.org/10.1039/c4cs00084f
  7. Agraıt, N., Yeyati, A. L., Van Ruitenbeek, J. M. (2003). Quantum properties of atomic-sized conductors. Physics Reports, 377 (2-3), 81–279. doi: https://doi.org/10.1016/s0370-1573(02)00633-6
  8. Sørensen, H. H. B., Hansen, P. C., Petersen, D. E., Skelboe, S., Stokbro, K. (2009). Efficient wave-function matching approach for quantum transport calculations. Physical Review B, 79 (20). doi: https://doi.org/10.1103/physrevb.79.205322
  9. Nitzan, A., Ratner, M. A. (2003). Electron Transport in Molecular Wire Junctions. Science, 300 (5624), 1384–1389. doi: https://doi.org/10.1126/science.1081572
  10. Ke, Y., Xia, K., Guo, H. (2008). Disorder Scattering in Magnetic Tunnel Junctions: Theory of Nonequilibrium Vertex Correction. Physical Review Letters, 100 (16). doi: https://doi.org/10.1103/physrevlett.100.166805
  11. Markussen, T., Rurali, R., Jauho, A.-P., Brandbyge, M. (2007). Scaling Theory Put into Practice: First-Principles Modeling of Transport in Doped Silicon Nanowires. Physical Review Letters, 99 (7). doi: https://doi.org/10.1103/physrevlett.99.076803
  12. Nozaki, D., Pastawski, H. M., Cuniberti, G. (2010). Controlling the conductance of molecular wires by defect engineering. New Journal of Physics, 12 (6), 063004. doi: https://doi.org/10.1088/1367-2630/12/6/063004
  13. Khater, A., Szczęśniak, D. (2011). A simple analytical model for electronic conductance in a one dimensional atomic chain across a defect. Journal of Physics: Conference Series, 289, 012013. doi: https://doi.org/10.1088/1742-6596/289/1/012013
  14. Szczęśniak, D., Khater, A. (2012). Electronic conductance via atomic wires: a phase field matching theory approach. The European Physical Journal B, 85 (6). doi: https://doi.org/10.1140/epjb/e2012-21055-x
  15. Belayadi, A., Bourahla, B., Mekideche-Chafa, F. (2018). Localized electronic surface states in metallic structureS. Surface Review and Letters, 25 (5), 1850101. doi: https://doi.org/10.1142/s0218625x18501019
  16. Büttiker, M. (1986). Four-Terminal Phase-Coherent Conductance. Physical Review Letters, 57 (14), 1761–1764. doi: https://doi.org/10.1103/physrevlett.57.1761
  17. Landauer, R. (1957). Spatial Variation of Currents and Fields Due to Localized Scatterers in Metallic Conduction. IBM Journal of Research and Development, 1 (3), 223–231. doi: https://doi.org/10.1147/rd.13.0223
  18. Khomyakov, P. A., Brocks, G., Karpan, V., Zwierzycki, M., Kelly, P. J. (2005). Conductance calculations for quantum wires and interfaces: Mode matching and Green’s functions. Physical Review B, 72 (3). doi: https://doi.org/10.1103/physrevb.72.035450
  19. Mardaani, M., Rabani, H., Esmaeili, A. (2011). An analytical study on electronic density of states and conductance of typical nanowires. Solid State Communications, 151 (13), 928–932. doi: https://doi.org/10.1016/j.ssc.2011.04.010
  20. Rabani, H., Mardaani, M. (2012). Exact analytical results on electronic transport of conjugated polymer junctions: Renormalization method. Solid State Communications, 152 (3), 235–239. doi: https://doi.org/10.1016/j.ssc.2011.09.026
  21. Wu, Y., Childs, P. (2010). Conductance of Graphene Nanoribbon Junctions and the Tight Binding Model. Nanoscale Research Letters, 6 (1). doi: https://doi.org/10.1007/s11671-010-9791-y
  22. Slater, J. C., Koster, G. F. (1954). Simplified LCAO Method for the Periodic Potential Problem. Physical Review, 94 (6), 1498–1524. doi: https://doi.org/10.1103/physrev.94.1498
  23. Harrison, W. A. (2004). Elementary electronic structure (revised edition). World Scientific Publishing Company. doi: https://doi.org/10.1142/5432
  24. Wills, J. M., Harrison, W. A. (1984). Further studies on interionic interactions in simple metals and transition metals. Physical Review B, 29 (10), 5486–5490. doi: https://doi.org/10.1103/physrevb.29.5486
  25. Landauer, R. (1957). Spatial Variation of Currents and Fields Due to Localized Scatterers in Metallic Conduction. IBM Journal of Research and Development, 1 (3), 223–231. doi: https://doi.org/10.1147/rd.13.0223
  26. Belayadi, A., Bourahla, B. (2018). A theoretical model to compute the localized electronic states at the surface of hexagonal structures with different coupling orbitals. Surface Science, 675, 1–14. doi: https://doi.org/10.1016/j.susc.2018.04.005
  27. Bourahla, B., Nafa, O. (2016). Magnons Heat Transfer and Magnons Scattering in Magnetic Sandwich Lattices: Application to Fe/Gd(5)/Fe System. SPIN, 6 (3), 1650007. doi: https://doi.org/10.1142/s2010324716500077
  28. Bloch, F. (1929). Über die quantenmechanik der elektronen in kristallgittern. Zeitschrift für physik, 52 (7-8), 555–600. doi: https://doi.org/10.1007/bf01339455
  29. Feuchtwang, T. E. (1967). Dynamics of a Semi-Infinite Crystal Lattice in a Quasiharmonic Approximation. II. The Normal-Mode Analysis of a Semi-Infinite Lattice. Physical Review, 155 (3), 731–744. doi: https://doi.org/10.1103/physrev.155.731
  30. Szeftel, J., Khater, A. (1987). Calculation of surface phonons and resonances: the matching procedure revisited: I. Journal of Physics C: Solid State Physics, 20 (29), 4725–4736. doi: https://doi.org/10.1088/0022-3719/20/29/010
  31. Szczȩśniak, D., Khater, A., Ba̧k, Z., Szczȩśniak, R., Ghantous, M. A. (2012). Quantum conductance of silicon-doped carbon wire nanojunctions. Nanoscale Research Letters, 7 (1). doi: https://doi.org/10.1186/1556-276x-7-616
  32. Khater, A., Belhadi, M., Abou Ghantous, M. (2011). Phonons heat transport at an atomic well boundary in ultrathin solid films. The European Physical Journal B, 80 (3), 363–369. doi: https://doi.org/10.1140/epjb/e2011-10892-8
  33. Khater, A., Bourahla, B., Abou Ghantous, M., Tigrine, R., Chadli, R. (2011). Magnons coherent transmission and heat transport at ultrathin insulating ferromagnetic nanojunctions. The European Physical Journal B, 82 (1), 53–61. doi: https://doi.org/10.1140/epjb/e2011-10935-2
  34. Grimech, H., Khater, A. (1995). Calculation of the spectral densities of the surface alloy system (PtcCu1 – c1/Cu(100). Surface Science, 323 (3), 198–206. doi: https://doi.org/10.1016/0039-6028(94)00630-x
  35. Economou, E. N. (2006). Green's functions in quantum physics. Vol. 7. Springer Science & Business Media. doi: https://doi.org/10.1007/3-540-28841-4
  36. Pastawski, H. M., Medina, E. (2001). Tight Binding'methods in quantum transport through molecules and small devices: From the coherent to the decoherent description. doi: https://doi.org/10.48550/arXiv.cond-mat/0103219
Consideration of electronic mean heat transport via a low dimension system

##submission.downloads##

Опубліковано

2024-04-11

Як цитувати

Aicha, Z., Sakher, E., Rachid, T., Abdallah, B., & Benselhoub, A. (2024). Розгляд електронного середнього транспорту тепла через систему низького розміру. Technology Audit and Production Reserves, 2(1(76), 31–41. https://doi.org/10.15587/2706-5448.2024.300260

Номер

Том 2 № 1(76) (2024): Виробничо-технологічні системи

Розділ

Матеріалознавство

Ліцензія

Авторське право (c) 2024 Zouaneb Aicha, Elfahem Sakher, Tigrine Rachid, Bendoura Abdallah, Aissa Benselhoub

Creative Commons License

Ця робота ліцензується відповідно до Creative Commons Attribution 4.0 International License.

Закріплення та умови передачі авторських прав (ідентифікація авторства) здійснюється у Ліцензійному договорі. Зокрема, автори залишають за собою право на авторство свого рукопису та передають журналу право першої публікації цієї роботи на умовах ліцензії Creative Commons CC BY. При цьому вони мають право укладати самостійно додаткові угоди, що стосуються неексклюзивного поширення роботи у тому вигляді, в якому вона була опублікована цим журналом, але за умови збереження посилання на першу публікацію статті в цьому журналі.