Research and analysis of tower crane load behavior when the rope breaks
DOI:
https://doi.org/10.15587/2706-5448.2024.302248Keywords:
tower crane, sling break, two-link pendulum, load swinging, Lagrange equation, nonlinear differential equationsAbstract
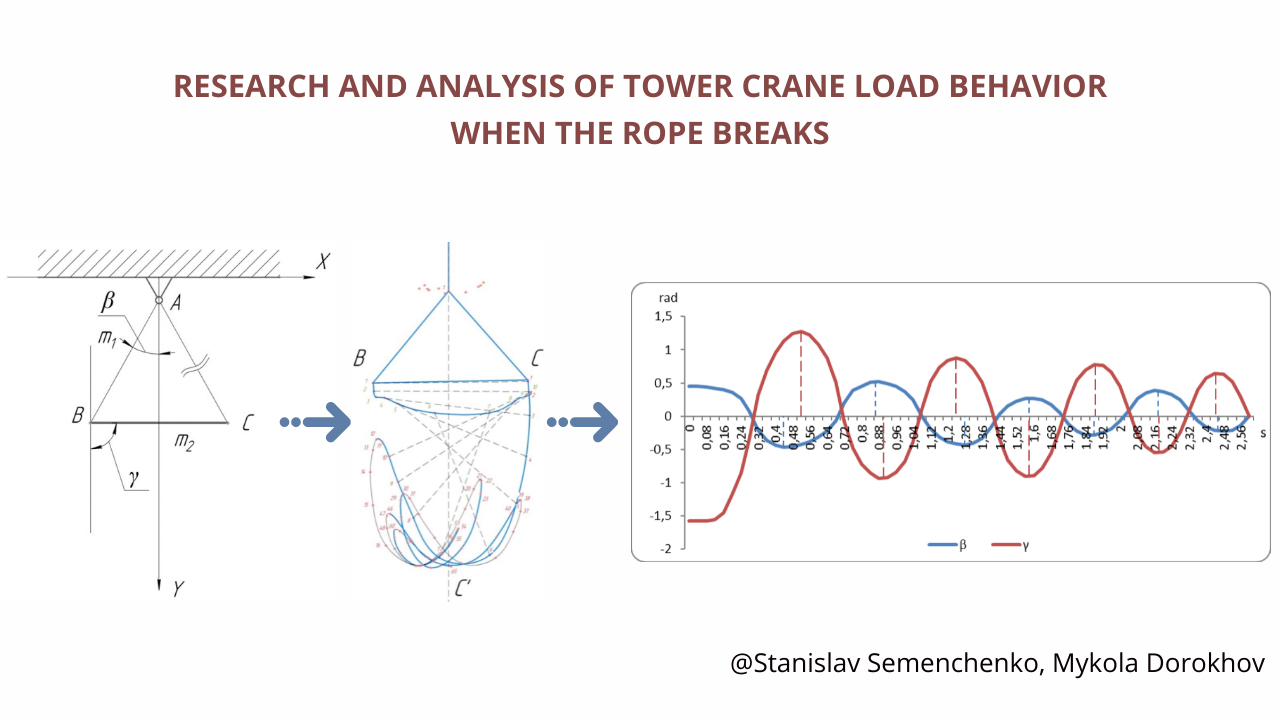
The object of research is the behavior of the load of the tower crane during the break of the sling. One of the most problematic areas is the safety of work and the prevention of emergency situations. Despite the presence of mandatory safety measures, during cargo transportation, one of the sling branches may be destroyed due to the presence of a dynamic component during the operation of the crane, or errors of the slinger when securing the cargo. Also, the presence of hidden internal or unnoticed defects in the sling construction itself cannot be ruled out. Also, one of the most problematic places is the chaotic fluctuations of the load, which negatively affect the stability of the crane and safety. The paper describes the case of the destruction of one of the branches of a two-rope sling during the transportation of a long product by a tower crane.
The proposed method of cargo behavior analysis is based on the use of a dynamic description of cable system failure modes within the framework of setting and solving differential-algebraic equations. This makes it possible to more accurately describe the behavior of the cargo when the sling breaks.
The obtained results show that the application of the proposed method makes it possible to bring the mathematical model of the two-link mathematical pendulum significantly closer to the actual mutual oscillations of the load during the sling break. This is due to the fact that the proposed method has a number of features, in particular, high sensitivity to changes in the behavior of the cargo and a quick reaction to a rope break.
These results can be used in practice in the design and operation of tower cranes. Thanks to the application of the proposed method, it is possible to obtain accurate values of cargo behavior indicators and timely detection of a rope break. Compared to similar known methods, this method has such advantages as high efficiency, reliability and safety of operation.
References
- Semeniuk, V. F., Stukalenko, M. I., Stukalenko, A. M. (1997). Opredelenie dinamicheskikh nagruzok v mostovom krane pri obryve kanata. Trudy Odesskogo politekhnicheskogo universiteta, 1, 94–97.
- Stukalenko, M. I. (2009). Povyshenie nadezhnosti uderzhaniia gruza pri obryve kanata v mostovom krane. Bezopasnost truda v promyshlennosti, 5, 21–25.
- Loveikin, V. S., Nesterov, A. P. (2002). Dinamicheskaia optimizatciia podemnykh mashin. Lugansk: Vid-vo SNU, 368.
- Loveikіn, V. S., Romasevich, Iu. O. (2011). Kompleksnyi sintez optimalnogo upravleniia dvizheniem gruzopodemnogo krana. Avtomatizatciia proizvodstvennykh protcessov v mashinostroenii i priborostroenii, 45, 385–399.
- Shamolin, M. V. (2008). Dinamicheskie sistemy s peremennoi dissipatciei: podkhody, metody, prilozheniia. Fundamentalna ta prikladna matematika, 3 (14), 32–37.
- Espíndola, R., Del Valle, G., Hernández, G., Pineda, I., Muciño, D., Díaz, P., Guijosa, S. (2019). The Double Pendulum of Variable Mass: Numerical Study for different cases. Journal of Physics: Conference Series, 1221 (1), 012049. doi: https://doi.org/10.1088/1742-6596/1221/1/012049
- Pravyla okhorony pratsi pid chas ekspluatatsii pidiomnykh kraniv, pidiomnykh prystroiv ta vidpovidnoho obladnannia: NPAOP 0.00-1.80-18: zaminiuie NPAOP 0.00-1.01-07 (2018). Zatv. Ministerstvo sotsialnoi polityky Ukrainy 19.01.2018. Kyiv: Ministerstvo sotsialnoi polityky Ukrainy, 214.
- Kwiatkowski, R., Hoffmann, T. J., Kołodziej, A. (2017). Dynamics of a Double Mathematical Pendulum with Variable Mass in Dimensionless Coordinates. Procedia Engineering, 177, 439–443. doi: https://doi.org/10.1016/j.proeng.2017.02.242
- Li, D., Xie, T., Li, G., Yao, J., Hu, S. (2024). Adaptive coupling tracking control strategy for double-pendulum bridge crane with load hoisting/lowering. Nonlinear Dynamics. doi: https://doi.org/10.1007/s11071-024-09474-2
- Alevras, P., Brown, I., Yurchenko, D. (2015). Experimental investigation of a rotating parametric pendulum. Nonlinear Dynamics, 81 (1-2), 201–213. doi: https://doi.org/10.1007/s11071-015-1982-8
- Radomski, A. P., Sierociński, D. J., Chiliński, B. D. (2024). Proposition of a structural health monitoring model for a concept of an innovative variable mass pendular tuned mass damper. Diagnostyka, 1–10. doi: https://doi.org/10.29354/diag/185458
Downloads
Published
How to Cite
Issue
Section
License
Copyright (c) 2024 Stanislav Semenchenko, Mykola Dorokhov

This work is licensed under a Creative Commons Attribution 4.0 International License.
The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.







