Кількісна оцінка волатильності цін на активи за допомогою дробового броунівського руху
DOI:
https://doi.org/10.15587/2706-5448.2025.329243Ключові слова:
фондовий ринок, дробовий броунівський рух, оцінювання параметрів, ринки з пам'яттю, волатильністьАнотація
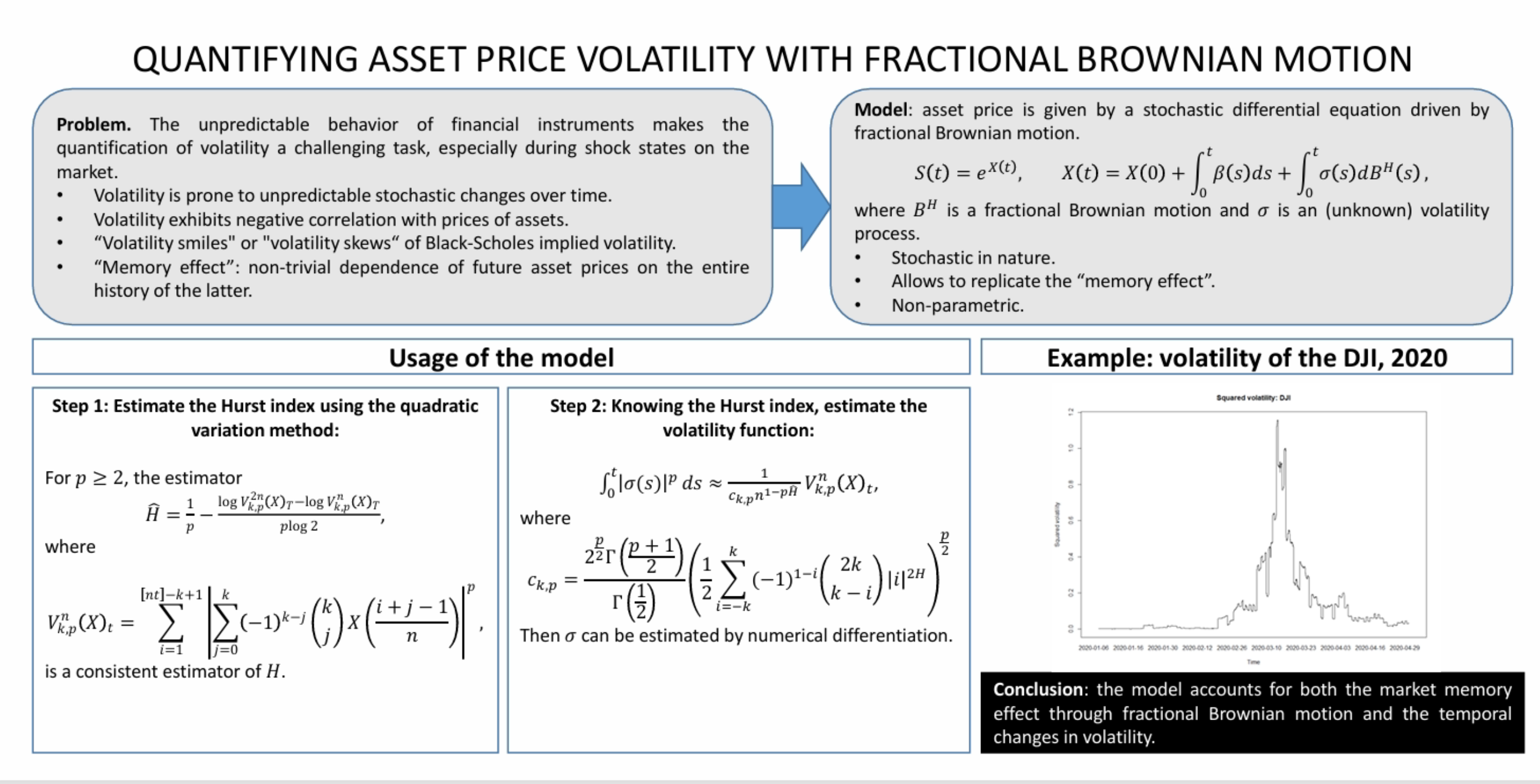
Об'єктом дослідження є поведінка волатильності фондового ринку у відповідь на раптові шоки та кризові коливання, з особливим акцентом на вивчення її складної часової структури та ефекту пам'яті. Одна з найбільших проблем у цій сфері полягає у стохастичній природі волатильності: вона розвивається нерегулярно в часі, її не можна безпосередньо спостерігати, та її потрібно оцінювати за непрямими показниками. Традиційні моделі, особливо ті, що ґрунтуються на класичному броунівському русі, часто не можуть точно відобразити таку динаміку, оскільки нехтують довгостроковою залежністю або «пам'яттю ринку», яка зазвичай спостерігається в реальних фінансових часових рядах. Цей недогляд може призвести до значних помилок в оцінці волатильності, особливо під час фаз ринкової турбулентності, таких як фінансові кризи або глобальні події.
Під час дослідження використано модель дробової дифузії для моделювання динаміки цін на активи, що включає залежну від часу та початково невідому функцію волатильності. Цей підхід ґрунтується на дробовому броунівському русі, немарковські властивості якого дозволяють моделі ефективно враховувати довгострокові кореляції в поведінці ринку. Для оцінки волатильності використано статистичні інструменти, засновані на p-варіаціях, що дозволило обчислити індекс Херста та реконструювати основний шлях реалізованої волатильності з високою чутливістю до структурних змін на ринку.
Показано, що цей метод значно підвищує точність відстеження волатильності, особливо в стресових умовах, таких як ті, що спостерігалися під час кризи 2020 року, викликаної COVID-19. Це пов'язано з тим, що запропонований метод має низку особливостей, зокрема здатність враховувати ефекти пам'яті та адаптивно реагувати на високочастотні варіації даних. Завдяки цьому вдається точніше вловлювати різкі стрибки волатильності та тривалу невизначеність на ринку. Порівняно зі стандартними моделями, досягнено таких переваг: покращена реакція на динаміку ринку, підвищена надійність прогнозів волатильності в кризові періоди та більш реалістичне відображення складності фінансового ринку.
Посилання
- Black, F., Scholes, M. (1973). The Pricing of Options and Corporate Liabilities. Journal of Political Economy, 81 (3), 637–654. https://doi.org/10.1086/260062
- Merton, R. C. (1973). Theory of Rational Option Pricing. The Bell Journal of Economics and Management Science, 4 (1), 141. https://doi.org/10.2307/3003143
- Samuelson, P. A. (1959). Rational theory of warrant pricing. Industrial Management Review, 6 (2), 13–39.
- Gatheral, J. (2006). The volatility surface: A practitioner’s guide. John Wiley & Sons.
- Hull, J. C. (2022). Options, futures, and other derivatives. Pearson.
- Fouque, J.-P., Papanicolaou, G., Sircar, K. R. (2000). Derivatives in financial markets with stochastic volatility. Cambridge University Press.
- Hagan, P. S., Kumar, D., Lesniewski, A., Woodward, D. E. (2002). Managing smile risk. Wilmott Magazine, 84–108.
- Renault, E., Touzi, N. (1996). Option hedging and implied volatilities in a stochastic volatility model1. Mathematical Finance, 6 (3), 279–302. https://doi.org/10.1111/j.1467-9965.1996.tb00117.x
- Cont, R. (2001). Empirical properties of asset returns: stylized facts and statistical issues. Quantitative Finance, 1 (2), 223–236. https://doi.org/10.1080/713665670
- Cont, R. (2005). Long range dependence in financial markets. Fractals in engineering. Springer-Verlag, 159–179. https://doi.org/10.1007/1-84628-048-6_11
- Cont, R. (2006). Volatility clustering in financial markets: Empirical facts and agent-based models. Long memory in economics. Berlin Heidelberg: Springer, 289–309. https://doi.org/10.1007/3-540-34625-2_10
- Cox, J. C. (1996). The Constant Elasticity of Variance Option Pricing Model. The Journal of Portfolio Management, 23 (5), 15–17. https://doi.org/10.3905/jpm.1996.015
- Heston, S. L. (1993). A Closed-Form Solution for Options with Stochastic Volatility with Applications to Bond and Currency Options. Review of Financial Studies, 6 (2), 327–343. https://doi.org/10.1093/rfs/6.2.327
- Anh, V., Inoue, A. (2005). Financial Markets with Memory I: Dynamic Models. Stochastic Analysis and Applications, 23 (2), 275–300. https://doi.org/10.1081/sap-200050096
- Beran, J. (1994). Statistics for long-memory processes. Chapman & Hall/CRC. Available at: https://www.routledge.com/Statistics-for-Long-Memory-Processes/Beran/p/book/9780412049019
- Bollerslev, T., Ole Mikkelsen, H. (1996). Modeling and pricing long memory in stock market volatility. Journal of Econometrics, 73 (1), 151–184. https://doi.org/10.1016/0304-4076(95)01736-4
- Breidt, F. J., Crato, N., de Lima, P. (1998). The detection and estimation of long memory in stochastic volatility. Journal of Econometrics, 83 (1-2), 325–348. https://doi.org/10.1016/s0304-4076(97)00072-9
- Ding, Z., Granger, C. W. J. (1996). Modeling volatility persistence of speculative returns: A new approach. Journal of Econometrics, 73 (1), 185–215. https://doi.org/10.1016/0304-4076(95)01737-2
- Ding, Z., Granger, C. W. J., Engle, R. F. (1993). A long memory property of stock market returns and a new model. Journal of Empirical Finance, 1 (1), 83–106. https://doi.org/10.1016/0927-5398(93)90006-d
- Chronopoulou, A., Viens, F. G. (2010). Estimation and pricing under long-memory stochastic volatility. Annals of Finance, 8 (2-3), 379–403. https://doi.org/10.1007/s10436-010-0156-4
- Comte, F., Coutin, L., Renault, E. (2010). Affine fractional stochastic volatility models. Annals of Finance, 8 (2-3), 337–378. https://doi.org/10.1007/s10436-010-0165-3
- Comte, F., Renault, E. (1998). Long memory in continuous‐time stochastic volatility models. Mathematical Finance, 8 (4), 291–323. https://doi.org/10.1111/1467-9965.00057
- Gatheral, J., Jaisson, T., Rosenbaum, M. (2014). Volatility is Rough. SSRN Electronic Journal. https://doi.org/10.2139/ssrn.2509457
- Harms, P., Stefanovits, D. (2019). Affine representations of fractional processes with applications in mathematical finance. Stochastic Processes and Their Applications, 129 (4), 1185–1228. https://doi.org/10.1016/j.spa.2018.04.010
- Zähle, M. (1998). Integration with respect to fractal functions and stochastic calculus. I. Probability Theory and Related Fields, 111 (3), 333–374. https://doi.org/10.1007/s004400050171
- Bishwal, J. P. N. (2008). Parameter Estimation in Stochastic Differential Equations. Lecture Notes in Mathematics. Springer Berlin Heidelberg. https://doi.org/10.1007/978-3-540-74448-1
- Kessler, M., Lindner, A., Sorensen, M. (2012). Statistical Methods for Stochastic Differential Equations. Whittles Publishing. https://doi.org/10.1201/b12126
- Kutoyants, Y. A. (2004). Statistical Inference for Ergodic Diffusion Processes. London: Springer. https://doi.org/10.1007/978-1-4471-3866-2
- Berzin, C., Latour, A., León, J. R. (2014). Inference on the Hurst Parameter and the Variance of Diffusions Driven by Fractional Brownian Motion. Lecture Notes in Statistics. Springer International Publishing. https://doi.org/10.1007/978-3-319-07875-5
- Hu, Y., Nualart, D., Zhou, H. (2017). Parameter estimation for fractional Ornstein – Uhlenbeck processes of general Hurst parameter. Statistical Inference for Stochastic Processes, 22 (1), 111–142. https://doi.org/10.1007/s11203-017-9168-2
- Manuel Corcuera, J., Nualart, D., Woerner, J. H. C. (2006). Power variation of some integral fractional processes. Bernoulli, 12 (4), 713–735. https://doi.org/10.3150/bj/1155735933
- Prakasa Rao, B. L. (2010). Statistical inference for fractional diffusion processes. Wiley-Blackwell. https://doi.org/10.1002/9780470667125
- Cheridito, P. (2003). Arbitrage in fractional Brownian motion models. Finance and Stochastics, 7 (4), 533–553. https://doi.org/10.1007/s007800300101
- Rogers, L. C. G. (1997). Arbitrage with Fractional Brownian Motion. Mathematical Finance, 7 (1), 95–105. https://doi.org/10.1111/1467-9965.00025
- Guasoni, P. (2006). No arbitrage under transaction costs, with fractional Brownian motion and beyond. Mathematical Finance, 16 (3), 569–582. https://doi.org/10.1111/j.1467-9965.2006.00283.x
- Sottinen, T., Valkeila, E. (2003). On arbitrage and replication in the fractional Black–Scholes pricing model. Statistics & Decisions, 21 (2-2003), 93–108. https://doi.org/10.1524/stnd.21.2.93.19003
##submission.downloads##
Опубліковано
Як цитувати
Номер
Розділ
Ліцензія
Авторське право (c) 2025 Maryna Iurchenko, Laura Šaltytė-Vaisiauskė, Vitalina Babenko

Ця робота ліцензується відповідно до Creative Commons Attribution 4.0 International License.
Закріплення та умови передачі авторських прав (ідентифікація авторства) здійснюється у Ліцензійному договорі. Зокрема, автори залишають за собою право на авторство свого рукопису та передають журналу право першої публікації цієї роботи на умовах ліцензії Creative Commons CC BY. При цьому вони мають право укладати самостійно додаткові угоди, що стосуються неексклюзивного поширення роботи у тому вигляді, в якому вона була опублікована цим журналом, але за умови збереження посилання на першу публікацію статті в цьому журналі.








