Quantifying asset price volatility with fractional Brownian motion
DOI:
https://doi.org/10.15587/2706-5448.2025.329243Keywords:
stock market, fractional Brownian motion, parameter estimation, markets with memory, volatilityAbstract
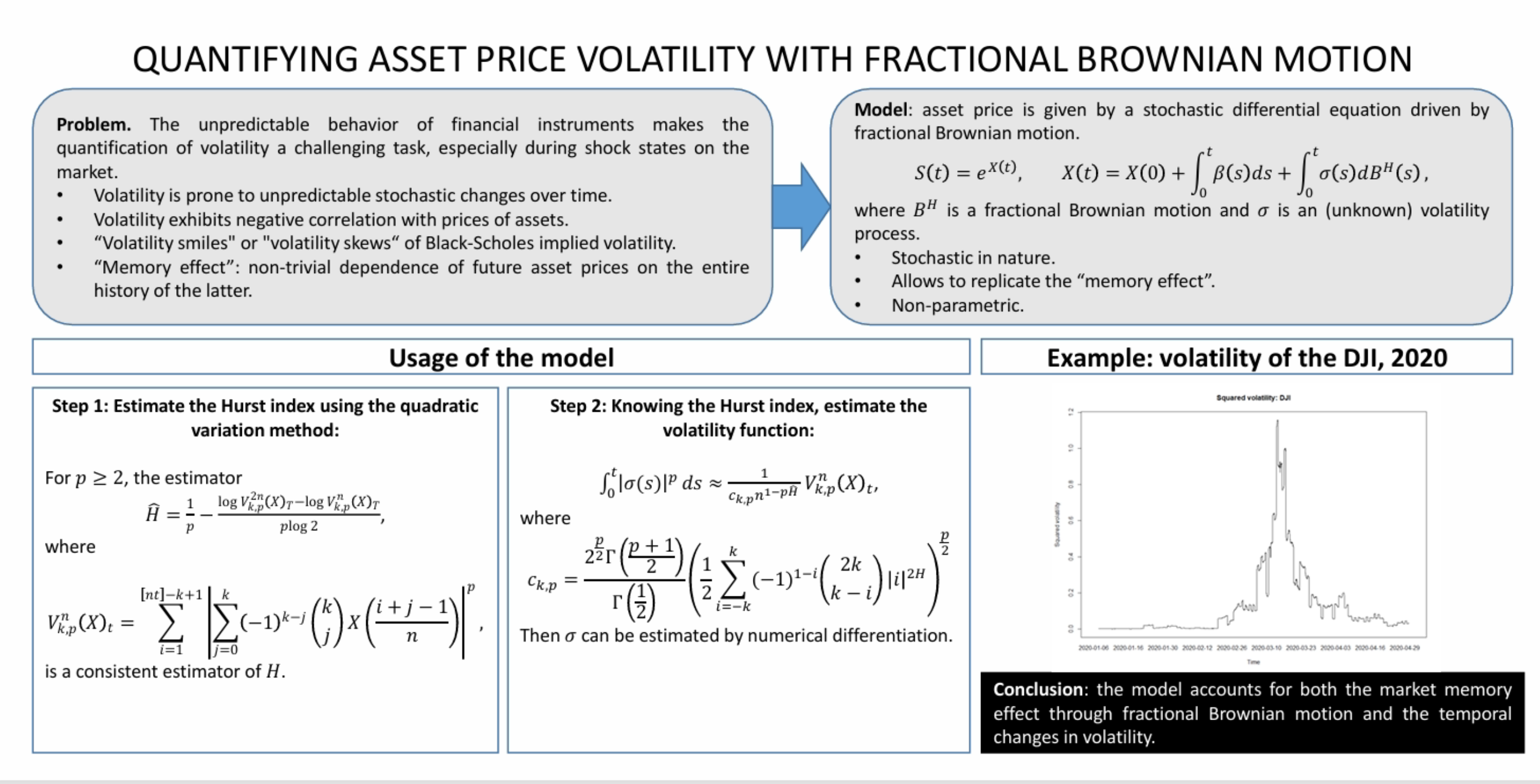
The object of the study is the behavior of stock market volatility in response to sudden shocks and crisis-driven fluctuations, with a specific focus on capturing its complex temporal structure and memory effects. One of the biggest challenges in this domain lies in the inherent stochastic nature of volatility: it evolves irregularly over time, cannot be directly observed, and must be estimated from indirect indicators. Conventional models, particularly those grounded in classical Brownian motion, often fall short in accurately representing such dynamics, as they neglect the long-range dependence – or “market memory” – commonly observed in real financial time series. This oversight can lead to significant errors in volatility estimation, especially during phases of market turbulence such as financial crises or global events.
A fractional diffusion framework was used during the study to model asset price dynamics, incorporating a time-dependent and initially unknown volatility function. This approach relies on fractional Brownian motion, whose non-Markovian properties enable the model to effectively account for long-term correlations in market behavior. To estimate the volatility, it is possible to employ statistical tools based on p-variations, which allowed to compute the Hurst index and reconstruct the underlying path of realized volatility with high sensitivity to structural market changes.
It is possible to obtain that this method significantly improves the accuracy of volatility tracking, particularly under stress conditions, such as those observed during the 2020 COVID-19 crisis. It is connected to the fact that the suggested method has a number of features, in particular its ability to incorporate memory effects and to respond adaptively to high-frequency data variations. Thanks to that, let’s manage to capture abrupt volatility spikes and sustained market uncertainty more precisely. Compared to the standard models, it is possible to achieve the following advantages: enhanced responsiveness to market dynamics, improved reliability of volatility forecasts during crisis periods, and a more realistic reflection of financial market complexity.
References
- Black, F., Scholes, M. (1973). The Pricing of Options and Corporate Liabilities. Journal of Political Economy, 81 (3), 637–654. https://doi.org/10.1086/260062
- Merton, R. C. (1973). Theory of Rational Option Pricing. The Bell Journal of Economics and Management Science, 4 (1), 141. https://doi.org/10.2307/3003143
- Samuelson, P. A. (1959). Rational theory of warrant pricing. Industrial Management Review, 6 (2), 13–39.
- Gatheral, J. (2006). The volatility surface: A practitioner’s guide. John Wiley & Sons.
- Hull, J. C. (2022). Options, futures, and other derivatives. Pearson.
- Fouque, J.-P., Papanicolaou, G., Sircar, K. R. (2000). Derivatives in financial markets with stochastic volatility. Cambridge University Press.
- Hagan, P. S., Kumar, D., Lesniewski, A., Woodward, D. E. (2002). Managing smile risk. Wilmott Magazine, 84–108.
- Renault, E., Touzi, N. (1996). Option hedging and implied volatilities in a stochastic volatility model1. Mathematical Finance, 6 (3), 279–302. https://doi.org/10.1111/j.1467-9965.1996.tb00117.x
- Cont, R. (2001). Empirical properties of asset returns: stylized facts and statistical issues. Quantitative Finance, 1 (2), 223–236. https://doi.org/10.1080/713665670
- Cont, R. (2005). Long range dependence in financial markets. Fractals in engineering. Springer-Verlag, 159–179. https://doi.org/10.1007/1-84628-048-6_11
- Cont, R. (2006). Volatility clustering in financial markets: Empirical facts and agent-based models. Long memory in economics. Berlin Heidelberg: Springer, 289–309. https://doi.org/10.1007/3-540-34625-2_10
- Cox, J. C. (1996). The Constant Elasticity of Variance Option Pricing Model. The Journal of Portfolio Management, 23 (5), 15–17. https://doi.org/10.3905/jpm.1996.015
- Heston, S. L. (1993). A Closed-Form Solution for Options with Stochastic Volatility with Applications to Bond and Currency Options. Review of Financial Studies, 6 (2), 327–343. https://doi.org/10.1093/rfs/6.2.327
- Anh, V., Inoue, A. (2005). Financial Markets with Memory I: Dynamic Models. Stochastic Analysis and Applications, 23 (2), 275–300. https://doi.org/10.1081/sap-200050096
- Beran, J. (1994). Statistics for long-memory processes. Chapman & Hall/CRC. Available at: https://www.routledge.com/Statistics-for-Long-Memory-Processes/Beran/p/book/9780412049019
- Bollerslev, T., Ole Mikkelsen, H. (1996). Modeling and pricing long memory in stock market volatility. Journal of Econometrics, 73 (1), 151–184. https://doi.org/10.1016/0304-4076(95)01736-4
- Breidt, F. J., Crato, N., de Lima, P. (1998). The detection and estimation of long memory in stochastic volatility. Journal of Econometrics, 83 (1-2), 325–348. https://doi.org/10.1016/s0304-4076(97)00072-9
- Ding, Z., Granger, C. W. J. (1996). Modeling volatility persistence of speculative returns: A new approach. Journal of Econometrics, 73 (1), 185–215. https://doi.org/10.1016/0304-4076(95)01737-2
- Ding, Z., Granger, C. W. J., Engle, R. F. (1993). A long memory property of stock market returns and a new model. Journal of Empirical Finance, 1 (1), 83–106. https://doi.org/10.1016/0927-5398(93)90006-d
- Chronopoulou, A., Viens, F. G. (2010). Estimation and pricing under long-memory stochastic volatility. Annals of Finance, 8 (2-3), 379–403. https://doi.org/10.1007/s10436-010-0156-4
- Comte, F., Coutin, L., Renault, E. (2010). Affine fractional stochastic volatility models. Annals of Finance, 8 (2-3), 337–378. https://doi.org/10.1007/s10436-010-0165-3
- Comte, F., Renault, E. (1998). Long memory in continuous‐time stochastic volatility models. Mathematical Finance, 8 (4), 291–323. https://doi.org/10.1111/1467-9965.00057
- Gatheral, J., Jaisson, T., Rosenbaum, M. (2014). Volatility is Rough. SSRN Electronic Journal. https://doi.org/10.2139/ssrn.2509457
- Harms, P., Stefanovits, D. (2019). Affine representations of fractional processes with applications in mathematical finance. Stochastic Processes and Their Applications, 129 (4), 1185–1228. https://doi.org/10.1016/j.spa.2018.04.010
- Zähle, M. (1998). Integration with respect to fractal functions and stochastic calculus. I. Probability Theory and Related Fields, 111 (3), 333–374. https://doi.org/10.1007/s004400050171
- Bishwal, J. P. N. (2008). Parameter Estimation in Stochastic Differential Equations. Lecture Notes in Mathematics. Springer Berlin Heidelberg. https://doi.org/10.1007/978-3-540-74448-1
- Kessler, M., Lindner, A., Sorensen, M. (2012). Statistical Methods for Stochastic Differential Equations. Whittles Publishing. https://doi.org/10.1201/b12126
- Kutoyants, Y. A. (2004). Statistical Inference for Ergodic Diffusion Processes. London: Springer. https://doi.org/10.1007/978-1-4471-3866-2
- Berzin, C., Latour, A., León, J. R. (2014). Inference on the Hurst Parameter and the Variance of Diffusions Driven by Fractional Brownian Motion. Lecture Notes in Statistics. Springer International Publishing. https://doi.org/10.1007/978-3-319-07875-5
- Hu, Y., Nualart, D., Zhou, H. (2017). Parameter estimation for fractional Ornstein – Uhlenbeck processes of general Hurst parameter. Statistical Inference for Stochastic Processes, 22 (1), 111–142. https://doi.org/10.1007/s11203-017-9168-2
- Manuel Corcuera, J., Nualart, D., Woerner, J. H. C. (2006). Power variation of some integral fractional processes. Bernoulli, 12 (4), 713–735. https://doi.org/10.3150/bj/1155735933
- Prakasa Rao, B. L. (2010). Statistical inference for fractional diffusion processes. Wiley-Blackwell. https://doi.org/10.1002/9780470667125
- Cheridito, P. (2003). Arbitrage in fractional Brownian motion models. Finance and Stochastics, 7 (4), 533–553. https://doi.org/10.1007/s007800300101
- Rogers, L. C. G. (1997). Arbitrage with Fractional Brownian Motion. Mathematical Finance, 7 (1), 95–105. https://doi.org/10.1111/1467-9965.00025
- Guasoni, P. (2006). No arbitrage under transaction costs, with fractional Brownian motion and beyond. Mathematical Finance, 16 (3), 569–582. https://doi.org/10.1111/j.1467-9965.2006.00283.x
- Sottinen, T., Valkeila, E. (2003). On arbitrage and replication in the fractional Black–Scholes pricing model. Statistics & Decisions, 21 (2-2003), 93–108. https://doi.org/10.1524/stnd.21.2.93.19003
Downloads
Published
How to Cite
Issue
Section
License
Copyright (c) 2025 Maryna Iurchenko, Laura Šaltytė-Vaisiauskė, Vitalina Babenko

This work is licensed under a Creative Commons Attribution 4.0 International License.
The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.







