Determination of analytical dependencies of distributed forces in a deformable wheel – deformable surface contact zone

Authors

DOI:

https://doi.org/10.15587/2706-5448.2025.329471

Keywords:

deformable wheel, deformable surface, soil compaction, contact surface, contact zone

Abstract

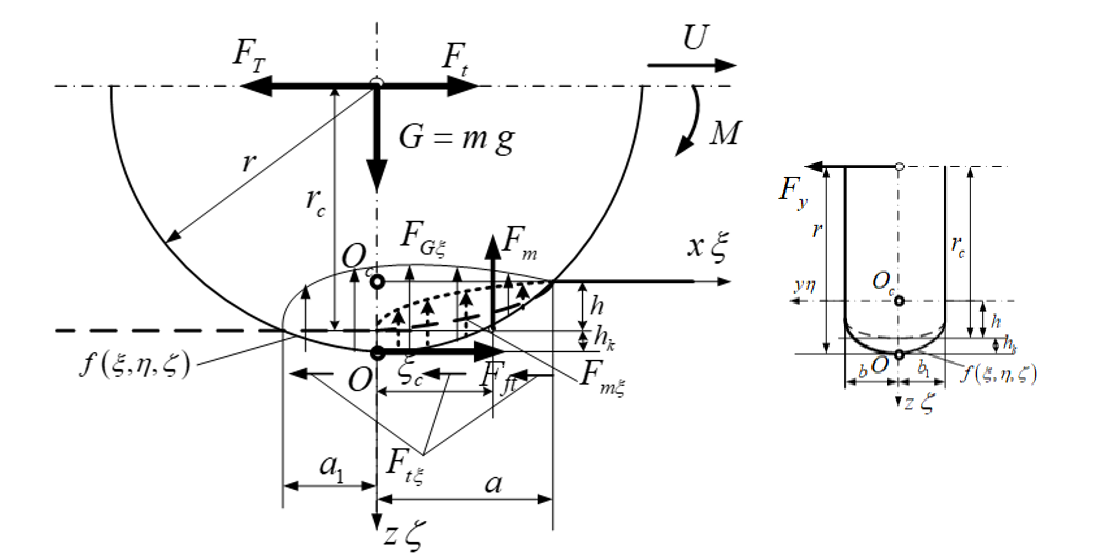
The object of this study is the contact interaction of two deformable bodies of inconsistent geometric shape, in particular, change in the stress-strain state of the wheel and the supporting surface. The significance of this topic arises from growing demands for vehicle mobility in difficult terrains, the necessity of minimizing environmental impact, and the need to optimize the design of mobile machinery components. A major challenge lies in developing a suitable analytical solution to define the stress-strain state variations within the contact zone between the wheel and soil or other surfaces.

This study employs an approach grounded in the fundamental principles of mathematical physics applied to elasticity theory problems. This enabled the derivation of analytical equations that describe the absolute deformations of both the surface and the wheel (tire), along with the contact pressure distribution. The pressure distribution within the contact zone was determined using the properties of surface integrals of the second kind. Concentrated forces, when related to the contact area, were equated to the integral value of this surface integral. The values of these distributed forces were then incorporated into the transformed Boussinesq and Cerruti potential equations.

The resulting analytical relationships can be utilized to determine the relative deformations of the contacting bodies and the stress distribution within them. Crucially, these relationships also serve as a basis for deriving equations that define the contact zone boundaries and the rolling resistance coefficient for deformable bodies. These derived relationships are general and presented in a form applicable to loads on both driving and passive (driven) wheels.

This proposed model offers substantially improved analytical accuracy over existing empirical methods. Moreover, these analytical dependencies help circumvent the computationally intensive calculations typically required by FEM (Finite Element Method) or DEM (Discrete Element Method) simulations for every unique loading scenario and material property set.

Author Biographies

Volodymyr Kovbasa, Poltava State Agrarian University

Doctor of Technical Sciences, Professor

Department of Mechanical and Electrical Engineering

Nataliia Priliepo, Poltava State Agrarian University

Department of Mechanical and Electrical Engineering

References

  1. Kushnarov, A. S., Kochev, V. I. (1989). Mekhaniko-tekhnologicheskie osnovy obrabotki pochvy. Kyiv: Urozhai, 144.
  2. Kovbasa, V. P. (2006). Mekhaniko-tekhnolohichne obgruntuvannia optymizatsii robochykh orhaniv z gruntom. [Doctoral dissertation; Natsionalnyi universytet bioresursiv i pryrodokorystuvannia Ukrainy]. Available at: https://uacademic.info/ua/document/0506U000111#!
  3. Koolen, A. J., Kuipers, H. (1983). Agricultural Soil Mechanics. Berlin: Springer-Verlag Berlin Heidelberg. https://doi.org/10.1007/978-3-642-69010-5
  4. Swamy, V. S., Pandit, R., Yerro, A., Sandu, C., Rizzo, D. M., Sebeck, K., Gorsich, D. (2023). Review of modeling and validation techniques for tire-deformable soil interactions. Journal of Terramechanics, 109, 73–92. https://doi.org/10.1016/j.jterra.2023.05.007
  5. Yang, W., Tiecheng, S., Yongjie, L., Chundi, S. (2016). Prediction for Tire – Pavement Contact Stress under Steady – State Conditions based on 3D Finite Element Method. Journal of Engineering Science and Technology Review, 9 (4), 17–25. https://doi.org/10.25103/jestr.094.04
  6. Xiao, W., Zhang, Y. (2016). Design of manned lunar rover wheels and improvement in soil mechanics formulas for elastic wheels in consideration of deformation. Journal of Terramechanics, 65, 61–71. https://doi.org/10.1016/j.jterra.2016.03.004
  7. Guthrie, A. G., Botha, T. R., Els, P. S. (2017). 3D contact patch measurement inside rolling tyres. Journal of Terramechanics, 69, 13–21. https://doi.org/10.1016/j.jterra.2016.09.004
  8. Yamashita, H., Jayakumar, P., Alsaleh, M., Sugiyama, H. (2017). Physics-Based Deformable Tire–Soil Interaction Model for Off-Road Mobility Simulation and Experimental Validation. Journal of Computational and Nonlinear Dynamics, 13 (2). https://doi.org/10.1115/1.4037994
  9. Bekker, M. G. (1969). Introduction to Terrain-Vehicle Systems. Ann Arbor: University of Michigan Press.
  10. Pacejka, H. B. (2012). Tire and Vehicle Dynamics. Butterworth-Heinemann. https://doi.org/10.1016/C2010-0-68548-8
  11. Kovbasa, V. P., Solomka, A. V., Spirin, A. V., Kucheruk, V. Yu., Karabekova, D. Zh., Khassenov, A. K. (2020). Theoretical determination of the distribution of forces and the size of the boundaries of the contact in the interaction of the deformable drive wheel with the soil. Bulletin of the Karaganda University “Physics Series”, 99 (3), 62–72. https://doi.org/10.31489/2020ph3/62-72
  12. Johnson, K. L. (1985). Contact Mechanics. London: Cambridge University Press. https://doi.org/10.1017/cbo9781139171731
  13. Wong, J. Y. (2022). Theory of Ground Vehicles. Hoboken: John Wiley & Sons. https://doi.org/10.1002/9781119719984
  14. Johnson, W., Mellor, P. B. (1973). Engineering plasticity. London, New York: Van Nostrand Reinhold Co.
  15. Kovbasa, V., Priliepo, N. (2024). Interactions of a Deformable Wheel with a Deformable Support Surface. International Journal of Innovative Technology and Exploring Engineering, 13 (9), 1–4. https://doi.org/10.35940/ijitee.i9944.13090824
Determination of analytical dependencies of distributed forces in a deformable wheel – deformable surface contact zone

Downloads

Published

2025-05-19

How to Cite

Kovbasa, V., & Priliepo, N. (2025). Determination of analytical dependencies of distributed forces in a deformable wheel – deformable surface contact zone. Technology Audit and Production Reserves, 3(1(83), 6–12. https://doi.org/10.15587/2706-5448.2025.329471

Issue

Vol. 3 No. 1(83) (2025): Industrial and technology systems

Section

Mechanics

License

Copyright (c) 2025 Volodymyr Kovbasa, Nataliia Priliepo

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.