Determination of analytical dependencies of distributed forces in a deformable wheel – deformable surface contact zone

Володимир Петрович Ковбаса; Наталія Володимирівна Прілєпо

doi:10.15587/2706-5448.2025.329471

Автор(и)

Володимир Петрович Ковбаса Полтавський державний аграрний університет, Україна https://orcid.org/0000-0003-4574-5826
Наталія Володимирівна Прілєпо Полтавський державний аграрний університет, Україна https://orcid.org/0000-0002-4182-7405

DOI:

https://doi.org/10.15587/2706-5448.2025.329471

Ключові слова:

деформівне колесо, деформівна поверхня, ущільнення ґрунту, поверхня контакту, зона контакту

Анотація

Об'єктом цього дослідження є контактна взаємодія двох деформівних тіл неузгодженої геометричної форми, зокрема, зміни напружено-деформованого стану колеса та опорної поверхні. Актуальність даної теми обумовлена зростанням вимог до прохідності техніки в складних умовах, необхідністю зниження негативного впливу на довкілля, а також потребою в оптимізації конструкцій рухомих елементів машин. Одним із найбільш складних питань є побудова адекватного аналітичного рішення для визначення змін напружено-деформованого стану в зоні контакту колеса з ґрунтовою або іншою поверхнею.

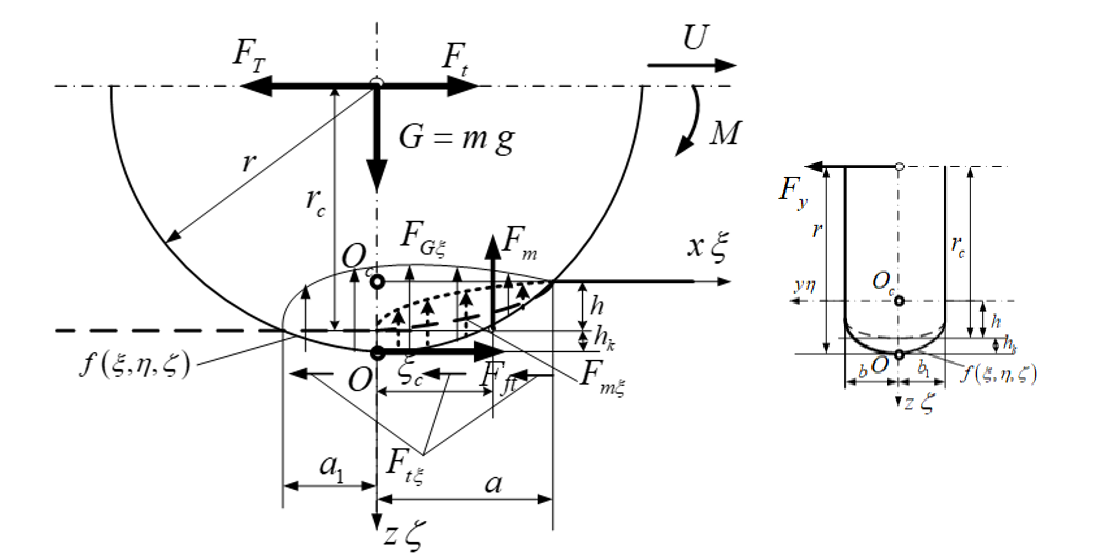
У цьому дослідженні застосовано підхід, заснований на основних положеннях математичної фізики, що використовуються при розв’язанні задач теорії пружності. Це дозволило вивести аналітичні рівняння для опису абсолютних деформацій поверхні та колеса (шини), розподілу контактного тиску та абсолютних деформацій. Розподіл тиску в зоні контакту був отриманий з використанням властивостей поверхневого інтеграла другого роду. При цьому зосереджені сили віднесені до площі контакту прирівнювались до інтегральної величини поверхневого інтегралу другого роду. Величини розподілених сил використовувались в перетворених рівняннях потенціалів Бусинеску та Черруті.

Отримані аналітичні залежності дозволяють використати їх для визначення відносних деформацій контактуючих тіл та розподілу напружень в них. Важливим є те, що ці аналітичні залежності дозволяють використати їх для отримання залежностей для визначення границь зони контакту та коефіцієнту тертя кочення для деформівних тіл. Отримані залежності мають загальний характер, оскільки представлені у загальному вигляді під дією навантажень як на ведуче колесо, так і на пасивне (ведене).

Запропонована модель забезпечує значне підвищення точності аналізу, в порівнянні з існуючими емпіричними підходами. Крім того, отримані залежності дозволять уникнути громіздких обчислень для кожного конкретного навантаження та кожного конкретного показника властивостей матеріалів методами FEM (finite element method) або DEM (discrete element method).

Біографії авторів

Володимир Петрович Ковбаса, Полтавський державний аграрний університет

Доктор технічних наук, професор

Кафедра механічної та електричної інженерії

Наталія Володимирівна Прілєпо, Полтавський державний аграрний університет

Кафедра механічної та електричної інженерії

Посилання

Kushnarov, A. S., Kochev, V. I. (1989). Mekhaniko-tekhnologicheskie osnovy obrabotki pochvy. Kyiv: Urozhai, 144.
Kovbasa, V. P. (2006). Mekhaniko-tekhnolohichne obgruntuvannia optymizatsii robochykh orhaniv z gruntom. [Doctoral dissertation; Natsionalnyi universytet bioresursiv i pryrodokorystuvannia Ukrainy]. Available at: https://uacademic.info/ua/document/0506U000111#!
Koolen, A. J., Kuipers, H. (1983). Agricultural Soil Mechanics. Berlin: Springer-Verlag Berlin Heidelberg. https://doi.org/10.1007/978-3-642-69010-5
Swamy, V. S., Pandit, R., Yerro, A., Sandu, C., Rizzo, D. M., Sebeck, K., Gorsich, D. (2023). Review of modeling and validation techniques for tire-deformable soil interactions. Journal of Terramechanics, 109, 73–92. https://doi.org/10.1016/j.jterra.2023.05.007
Yang, W., Tiecheng, S., Yongjie, L., Chundi, S. (2016). Prediction for Tire – Pavement Contact Stress under Steady – State Conditions based on 3D Finite Element Method. Journal of Engineering Science and Technology Review, 9 (4), 17–25. https://doi.org/10.25103/jestr.094.04
Xiao, W., Zhang, Y. (2016). Design of manned lunar rover wheels and improvement in soil mechanics formulas for elastic wheels in consideration of deformation. Journal of Terramechanics, 65, 61–71. https://doi.org/10.1016/j.jterra.2016.03.004
Guthrie, A. G., Botha, T. R., Els, P. S. (2017). 3D contact patch measurement inside rolling tyres. Journal of Terramechanics, 69, 13–21. https://doi.org/10.1016/j.jterra.2016.09.004
Yamashita, H., Jayakumar, P., Alsaleh, M., Sugiyama, H. (2017). Physics-Based Deformable Tire–Soil Interaction Model for Off-Road Mobility Simulation and Experimental Validation. Journal of Computational and Nonlinear Dynamics, 13 (2). https://doi.org/10.1115/1.4037994
Bekker, M. G. (1969). Introduction to Terrain-Vehicle Systems. Ann Arbor: University of Michigan Press.
Pacejka, H. B. (2012). Tire and Vehicle Dynamics. Butterworth-Heinemann. https://doi.org/10.1016/C2010-0-68548-8
Kovbasa, V. P., Solomka, A. V., Spirin, A. V., Kucheruk, V. Yu., Karabekova, D. Zh., Khassenov, A. K. (2020). Theoretical determination of the distribution of forces and the size of the boundaries of the contact in the interaction of the deformable drive wheel with the soil. Bulletin of the Karaganda University “Physics Series”, 99 (3), 62–72. https://doi.org/10.31489/2020ph3/62-72
Johnson, K. L. (1985). Contact Mechanics. London: Cambridge University Press. https://doi.org/10.1017/cbo9781139171731
Wong, J. Y. (2022). Theory of Ground Vehicles. Hoboken: John Wiley & Sons. https://doi.org/10.1002/9781119719984
Johnson, W., Mellor, P. B. (1973). Engineering plasticity. London, New York: Van Nostrand Reinhold Co.
Kovbasa, V., Priliepo, N. (2024). Interactions of a Deformable Wheel with a Deformable Support Surface. International Journal of Innovative Technology and Exploring Engineering, 13 (9), 1–4. https://doi.org/10.35940/ijitee.i9944.13090824