Дослідження руйнування ортотропних композитів із врахуванням їх структурної стохастичності
DOI:
https://doi.org/10.15587/2706-5448.2023.278121Ключові слова:
ортотропний композитний матеріал, надійність, стохастичність структури, руйнівне навантаження, функція розподілу, імовірність зруйнування, пластинаАнотація
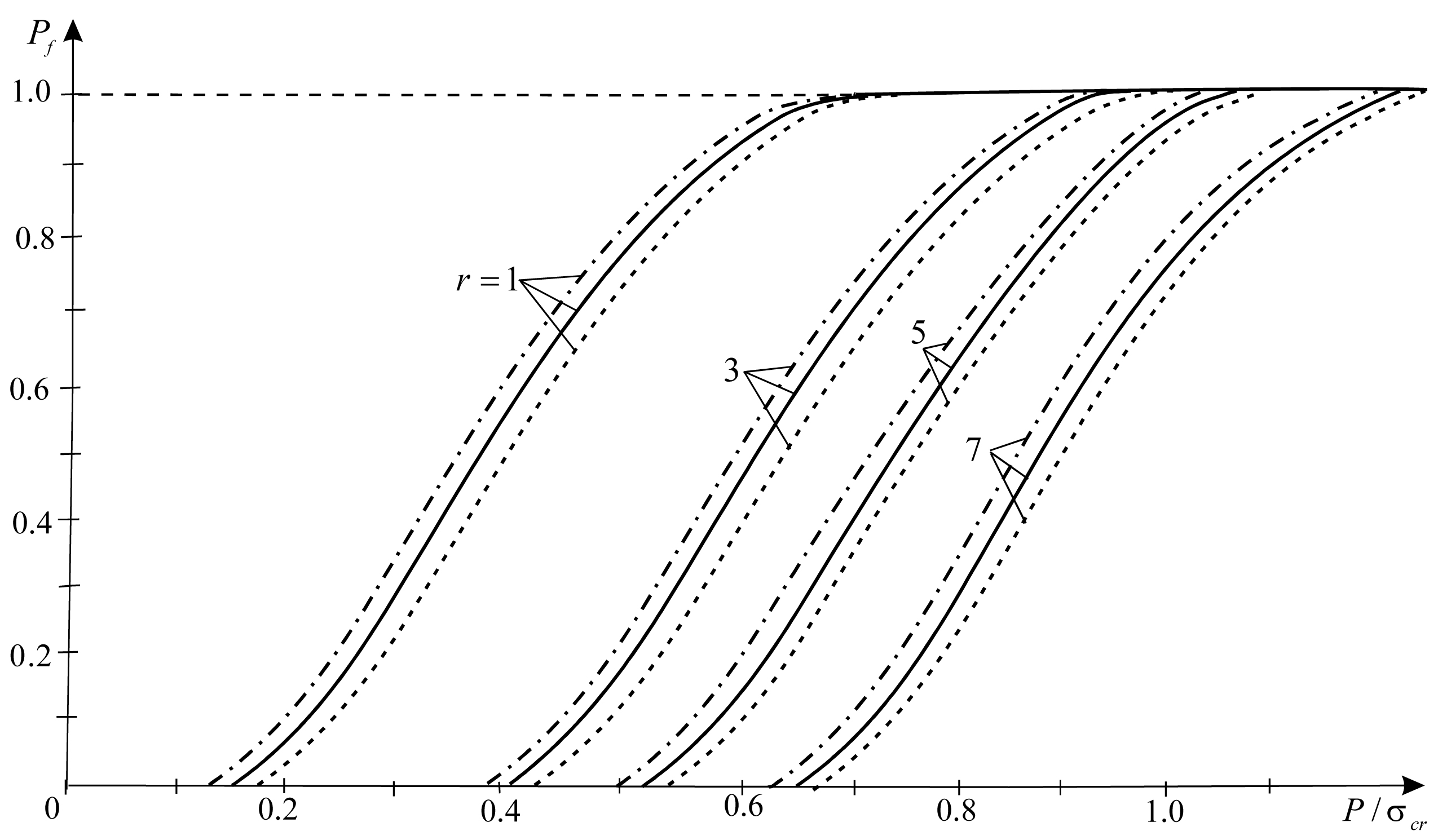
Об’єктом дослідження є побудова алгоритму оцінки надійності ортотропної композитної пластини з врахуванням стохастичності її структури за умов плоскої деформації. Пластина складається з матриці та елементів армування. Основні ортотропні напрямки матеріалу співпадають з напрямками дії навантаження. Проведені дослідження базуються на критерії руйнування, вираженого через компоненти макронапружень. Використовуємо гіпотезу найслабшої ланки, яка для випадку статистичної теорії міцності звучить так: граничне (руйнівне) навантаження для ортотропної композитної пластини дорівнює граничному навантаженню для її найслабшого елемента. Дефекти-тріщини характеризуються незалежними випадковими величинами – півдовжиною та кутом орієнтації між лінією дефекта та віссю ортотропії з більшим модулем пружності. Запропонованій моделі ортотропного композитного матеріалу відповідають відомі експериментальні дослідження епоксифенольного склопластику на кордній склотканині. Щільність розподілу ймовірностей орієнтації дефектів враховує їх переважаючу орієнтацію в напрямку армування. На базі отриманої інтегральної функції розподілу руйнівного навантаження композита здійснено побудову та дослідження діаграм залежності ймовірності руйнування пластин для різної кількості тріщин, структурної неоднорідності та типу прикладеного навантаження.
Комплексне застосування детерміністичного розв’язку механіки руйнування композитних матеріалів та методів теорії ймовірностей та математичної статистики дозволяє провести адекватнішу оцінку надійності композитних матеріалів з врахуванням стохастичності їх структури.
Основним змістом даної роботи є побудова та аналіз діаграм залежності ймовірності руйнування стохастично дефектних армованих композитних матеріалів.
Отримані результати дозволяють провести оцінку надійності ортотропних стохастично дефектних матеріалів за умов плоскої деформації.
Алгоритм сумісного поєднання дефектності та випадковості структури ортотропного композитного матеріалу дає змогу якісно дослідити його руйнування за різних видів прикладеного навантаження.
Посилання
- Onkar, A. K., Upadhyay, C. S., Yadav, D. (2007). Probabilistic failure of laminated composite plates using the stochastic finite element method. Composite Structures, 77 (1), 79–91. doi: https://doi.org/10.1016/j.compstruct.2005.06.006
- Sakata, S., Ashida, F., Enya, K. (2012). A Microscopic failure probability analysis of a unidirectional fiber reinforced composite material via a multiscale stochastic stress analysis for a microscopic random variation of an elastic property. Computational Materials Science, 62, 35–46. doi: https://doi.org/10.1016/j.commatsci.2012.05.008
- Gadade, A. M., Lal, A., Singh, B. (2016). Stochastic progressive failure analysis of laminated composite plates using Puck's failure criteria. Mechanics of Advanced Materials and Structures, 739–757. doi: https://doi.org/10.1080/15376494.2015.1029163
- Saberi, S., Abdollahi, A., Inam, F. (2021). Reliability analysis of bistable composite laminates. AIMS Materials Science, 8 (1), 29–41. doi: https://doi.org/10.3934/matersci.2021003
- Xu, J.-H., Zhou, G.-D., Zhu, T.-Y. (2021). Fatigue Reliability Assessment for Orthotropic Steel Bridge Decks Considering Load Sequence Effects. Frontiers in Materials, 8. doi: https://doi.org/10.3389/fmats.2021.678855
- Magar, A., Lal, A. (2021). Progressive failure analysis of laminated plate containing elliptical cutout. International Journal of Structural Integrity, 12 (4), 569–588. doi: https://doi.org/10.1108/ijsi-10-2020-0092
- Baitsar, R., Kvit, R. (2018). Method of the reliability calculation of orthotropic composite materials with random defects. ScienceRise, 10 (51), 28–32. doi: https://doi.org/10.15587/2313-8416.2018.146636
- Serensen, S. V., Zaitcev, G. P. (1982). Nesushchaia sposobnost tonkostennykh konstruktcii iz armirovannykh plastikov s defektami. Kyiv: Naukova dumka, 295.
- Vitvitckii, P. M., Popina, S. Iu. (1980). Prochnost i kriterii khrupkogo razrusheniia stokhasticheski defektnykh tel. Kyiv: Naukova dumka, 186.
- Deliavsky, M., Kvit, R. (1992). Macro-stress distribution near crack-like defects in anisotropic micro-inhomogeneous body under flat deformation and longitudinal displacement. Physicochemical Mechanics of Materials, 2, 50–54.
- Koroliuk, V. S., Portenko, N. I., Skorokhod, A. V., Turbin, A. F. (1985). Spravochnik po teorii veroiatnostei i matematicheskoi statistike. Moscow: Nauka, 640.
- Cheng, A. S., Laird, C. (1981). Fatigue life behaviour of copper single crystals. Part II: Model for crack nucleation in persistent slip bands. Fatigue & Fracture of Engineering Materials & Structures, 4, 343–353. doi: https://doi.org/10.1111/j.1460-2695.1981.tb01131.x
##submission.downloads##
Опубліковано
Як цитувати
Номер
Розділ
Ліцензія
Авторське право (c) 2023 Roman Kvit

Ця робота ліцензується відповідно до Creative Commons Attribution 4.0 International License.
Закріплення та умови передачі авторських прав (ідентифікація авторства) здійснюється у Ліцензійному договорі. Зокрема, автори залишають за собою право на авторство свого рукопису та передають журналу право першої публікації цієї роботи на умовах ліцензії Creative Commons CC BY. При цьому вони мають право укладати самостійно додаткові угоди, що стосуються неексклюзивного поширення роботи у тому вигляді, в якому вона була опублікована цим журналом, але за умови збереження посилання на першу публікацію статті в цьому журналі.








