Designing an object-oriented architecture for the finite element simulation of structural elements

Authors

DOI:

https://doi.org/10.15587/1729-4061.2022.268018

Keywords:

finite element method, object-oriented programming, design pattern, theory of elasticity, PyFEM

Abstract

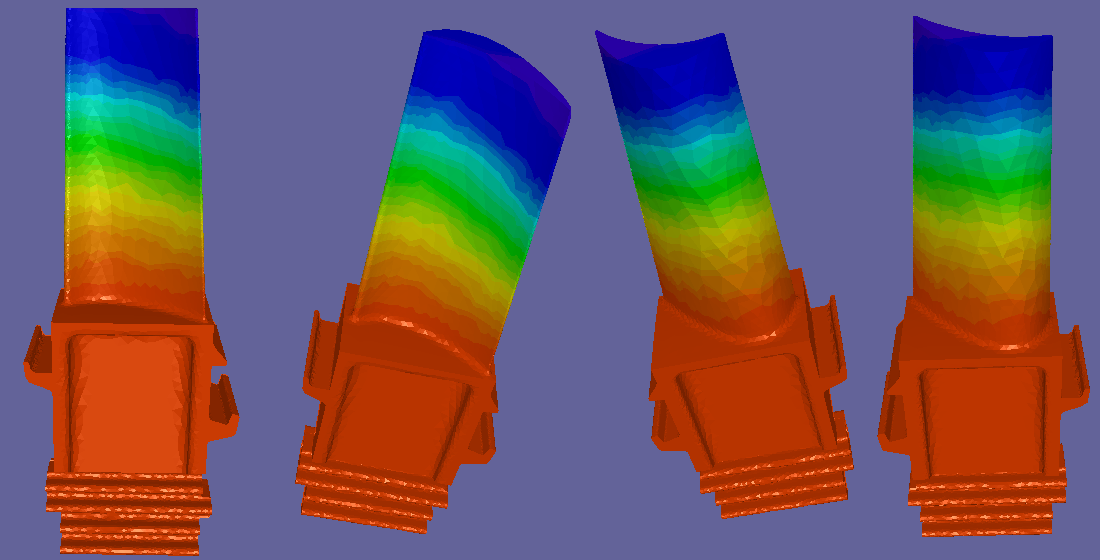
This paper reports the development of an architecture and software implementation of the library of classes for the finite-element analysis of problems in the theory of elasticity with an open-source code. The practical necessity of such systems is due to the fact that in modern equipment there are new types of materials whose structural elements' calculation has certain features. As a result, it is necessary to update the relevant scientific software or even devise a new one. A flexible software architecture is designed to reduce the time and complexity of such updates. Existing implementations of the method of finite elements with open source have been analyzed: it was revealed that there are no systems aimed at the most flexible and user-friendly architecture. The system of abstract classes proposed in the current work corresponds to known SOLID principles of object-oriented design and makes it possible to scale the already developed analysis program for new tasks in an easy and understandable way. To test the quality of the developed system from the point of view of software engineering, the maintainability index and cyclomatic complexity code metrics were used. The values of these metrics for the modules of the PyFEM system core vary in the following ranges: from 1 to 18 for the maintainability index, and from 22 to 100 for cyclomatic complexity. PyFEM testing was performed on the task of determining the stressed-strained state of the turbine rotor blade. Due to the ease of implementation, it was possible to build a set of effective and intuitive classes that make it possible to solve numerically the static and dynamic problems in the theory of elasticity. The developed class library can be used in the development of both universal and specialized software designed to analyze multiphysics problems.

Author Biographies

Oleksii Hniezdovskyi, National University "Zaporizhzhia Polytechnic"

Senior Lecturer

Department of Informational Technologies in Tourism

Oleksii Kudin, Zaporizhzhia National University

PhD, Associate Professor

Department of Software Engineering

Yuriy Belokon, Zaporizhzhia National University

Doctor of Technical Sciences, Associate Professor

Department of Pressure Metal Processing

Dmytro Kruglyak, Zaporizhzhia National University

PhD, Associate Professor

Department of Pressure Metal Processing

Sergii Ilin, Zaporizhzhia National University

PhD

Department of Thermal Power and Hydropower

References

  1. Breslavskyi, D. V., Korytko, Yu. M., Tatarinova, O. A. (2017). Proektuvannia ta rozrobka skinchennoelementnoho prohramnoho zabezpechennia. Kharkiv, 232. Available at: http://library.kpi.kharkov.ua/files/new_postupleniya/prropz.pdf
  2. Logg, A., Mardal, K.-A., Wells, G. (Eds.) (2012). Automated Solution of Differential Equations by the Finite Element Method. Lecture Notes in Computational Science and Engineering. doi: https://doi.org/10.1007/978-3-642-23099-8
  3. Choporov, S., Gomenyuk, S., Kudin, O., Lisnyak, A. (2018). Design patterns for object-oriented scientific software. CEUR Workshop Proceedings, 441–444. Available at: https://ceur-ws.org/Vol-2105/10000441.pdf
  4. Cimrman, R., Lukeš, V., Rohan, E. (2019). Multiscale finite element calculations in Python using SfePy. Advances in Computational Mathematics, 45 (4), 1897–1921. doi: https://doi.org/10.1007/s10444-019-09666-0
  5. Hecht, F. (2012). New development in freefem++. Journal of Numerical Mathematics, 20 (3-4). doi: https://doi.org/10.1515/jnum-2012-0013
  6. Xie, J., Ehmann, K., Cao, J. (2022). MetaFEM: A generic FEM solver by meta-expressions. Computer Methods in Applied Mechanics and Engineering, 394, 114907. doi: https://doi.org/10.1016/j.cma.2022.114907
  7. Renard, Y., Poulios, K. (2021). GetFEM: Automated FE Modeling of Multiphysics Problems Based on a Generic Weak Form Language. ACM Transactions on Mathematical Software, 47 (1), 1–31. doi: https://doi.org/10.1145/3412849
  8. Badia, S., Verdugo, F. (2020). Gridap: An extensible Finite Element toolbox in Julia. Journal of Open Source Software, 5 (52), 2520. doi: https://doi.org/10.21105/joss.02520
  9. Khara, B., Balu, A., Joshi, A., Sarkar, S., Hegde, C., Krishnamurthy, A., Ganapathysubramanian, B. (2021). NeuFENet: Neural Finite Element Solutions with Theoretical Bounds for Parametric PDEs. arXiv. doi: https://doi.org/10.48550/arXiv.2110.01601
  10. Mitusch, S. K., Funke, S. W., Kuchta, M. (2021). Hybrid FEM-NN models: Combining artificial neural networks with the finite element method. Journal of Computational Physics, 446, 110651. doi: https://doi.org/10.1016/j.jcp.2021.110651
  11. Uriarte, C., Pardo, D., Omella, Á. J. (2022). A Finite Element based Deep Learning solver for parametric PDEs. Computer Methods in Applied Mechanics and Engineering, 391, 114562. doi: https://doi.org/10.1016/j.cma.2021.114562
  12. Grementieri, L., Galeone, P. (2022). Towards Neural Sparse Linear Solvers. arXiv. doi: https://doi.org/10.48550/arXiv.2203.06944.
  13. Trushevskyi, V. M., Shynkarenko, H. A., Shcherbyna, N. M. (2014). Metod skinchennykh elementiv i shtuchni neironni merezhi. Liviv: LNU imeni Ivana Frankach, 396.
  14. Geuzaine, C., Remacle, J.-F. (2009). Gmsh: A 3-D finite element mesh generator with built-in pre- and post-processing facilities. International Journal for Numerical Methods in Engineering, 79 (11), 1309–1331. doi: https://doi.org/10.1002/nme.2579
  15. Netgen/NGSolve. Available at: https://ngsolve.org/
  16. Weisfeld, M. (2019). The Object-Oriented Thought Process. Addison-Wesley, 412.
  17. Ihnatchenko, M. S., Kudin, O. V., Gnezdovskiy, O. V. (2020). Object-oriented implementation of the finite element analysis library in the python programming language. Visnyk of Zaporizhzhya National University. Physical and Mathematical Sciences, 1, 138–147. doi: https://doi.org/10.26661/2413-6549-2020-1-18
  18. Turan, O., Tanriöver, Ö. Ö. (2018). An Experimental Evaluation of the Effect of SOLID Principles to Microsoft VS Code Metrics. AJIT-e: Online Academic Journal of Information Technology, 9 (34), 7–24. doi: https://doi.org/10.5824/1309-1581.2018.4.001.x
  19. Ranjan, A., Rakshith, A. (2021). Analysis of Industrial Gas Turbine Blade. International Research Journal of Engineering and Technology, 8 (5), 4247–4251.
  20. Yuriy, B., Aleksandr, Z., Karina, B. (2017). The investigation of nanostructure formation in intermetallic γ-TiAl alloys. 2017 IEEE International Young Scientists Forum on Applied Physics and Engineering (YSF). doi: https://doi.org/10.1109/ysf.2017.8126640
  21. Sereda, B., Sereda, D., Belokon, Y. (2015). Investigation of corrosion and oxidation of γ-TiAl alloys obtained in self propagating high temperature synthesis. Materials Science and Technology Conference and Exhibition. Vol. 2. Columbus, 1249–1255.
Designing an object-oriented architecture for the finite element simulation of structural elements

Downloads

Published

2022-12-30

How to Cite

Hniezdovskyi, O., Kudin, O., Belokon, Y., Kruglyak, D., & Ilin, S. (2022). Designing an object-oriented architecture for the finite element simulation of structural elements. Eastern-European Journal of Enterprise Technologies, 6(2 (120), 78–84. https://doi.org/10.15587/1729-4061.2022.268018

Issue

Vol. 6 No. 2 (120) (2022): Information technology. Industry control systems

Section

Information technology

License

Copyright (c) 2022 Oleksii Hniezdovskyi, Oleksii Kudin, Yuriy Belokon, Dmytro Kruglyak, Sergii Ilin

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.

A license agreement is a document in which the author warrants that he/she owns all copyright for the work (manuscript, article, etc.).
The authors, signing the License Agreement with TECHNOLOGY CENTER PC, have all rights to the further use of their work, provided that they link to our edition in which the work was published.
According to the terms of the License Agreement, the Publisher TECHNOLOGY CENTER PC does not take away your copyrights and receives permission from the authors to use and dissemination of the publication through the world's scientific resources (own electronic resources, scientometric databases, repositories, libraries, etc.).
In the absence of a signed License Agreement or in the absence of this agreement of identifiers allowing to identify the identity of the author, the editors have no right to work with the manuscript.
It is important to remember that there is another type of agreement between authors and publishers – when copyright is transferred from the authors to the publisher. In this case, the authors lose ownership of their work and may not use it in any way.