Determining experimentally the patterns of the manifestation of the Sommerfeld effect in a ball auto-balancer

Authors

DOI:

https://doi.org/10.15587/1729-4061.2022.265578

Keywords:

inertial vibration exciter, resonant vibratory machine, steady state motion, Sommerfeld effect, autobalancing, motion stability

Abstract

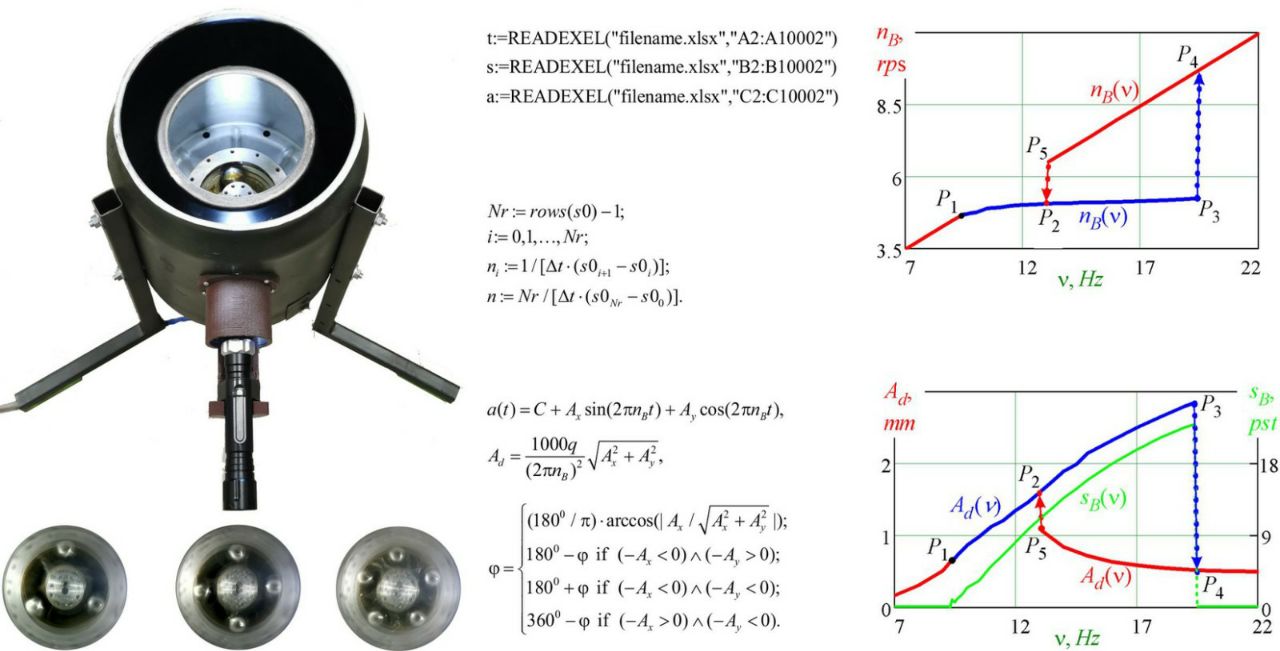
This paper proposes an experimental method for studying the Sommerfeld effect in auto-balancers or exciters of resonant vibrations of pendulum, ball, or roller type. The method is based on the processing of signals acquired from analog sensors of rotations and vibration acceleration using regression analysis. The method is tested on a specially designed rotor bench on isotropic viscoelastic supports, which executes spatial motion, and an auto-balancer with one ball.

Checking the accuracy of the method using stroboscopic lighting demonstrates the accuracy of determining the speed of rotation of the rotor, ball, oscillation frequency of the rotor, etc. with an error of several hundredths of a percent.

When fixing the ball relative to the rotor, a classic inertial vibration exciter is obtained. The rotor has two resonant velocities. The Sommerfeld effect is almost not manifested. With a gradual increase in the frequency of the current, the rotor speed increases monotonously. There is no significant slip or jump in the rotor speed. There are two distinct peaks on the amplitude-frequency characteristic. Therefore, such a vibration exciter is not suitable for the excitation of resonant vibrations.

With the free placement of the ball in the oil, the behavior of the system changes significantly in the vicinity of the first resonant velocity. The first narrow resonant peak disappears in the roto. Instead, there is a long, gentle resonant rise. It lasts at a current frequency of 9.4 Hz to 19.3 Hz. The amplitude at the reference point on the resonant rise increases from 0.7 mm to 2.84 mm. Therefore, by changing the frequency of the current, it is possible to smoothly change the amplitude of the rotor oscillations by almost 4 times. The maximum amplitude of rotor oscillations is the same as at the first resonance with a fixed ball. Due to the gentleness of the resonant rise, a freely installed ball itself is a reliable exciter of resonant vibrations

Author Biographies

Gennadiy Filimonikhin, Central Ukrainian National Technical University

Doctor of Technical Sciences, Professor, Head of Department

Department of Machine Parts and Applied Mechanics

Volodymyr Yatsun, Central Ukrainian National Technical University

PhD, Associate Professor

Department of Road Cars and Building

Anatolii Matsui, Central Ukrainian National Technical University

Doctor of Technical Sciences, Associate Professor

Department of Automation of Production Processes

Lubov Olijnichenko, Central Ukrainian National Technical University

PhD, Senior Lecturer

Department of Machine Parts and Applied Mechanics

Viktor Pukalov, Central Ukrainian National Technical University

PhD, Associate Professor

Department of Machine Parts and Applied Mechanics

References

  1. Sommerfeld, A. (1902). Beiträge zum dynamischen Ausbau der Festigkeitslehre. Zeitschrift des Vereines Deutscher Ingenieure, 46, 391–394.
  2. Blekhman, I. I. (2000). Vibrational mechanics: nonlinear dynamic effects, general approach, applications. World Scientific, 536. doi: https://doi.org/10.1142/4116
  3. Kononenko, V. O., IGladwell, G. M. L. (Ed.) (1969). Vibrating systems with a limited power supply. London: Iliffe, 236.
  4. Balthazar, J. M. (Ed.) (2022). Nonlinear Vibrations Excited by Limited Power Sources. Springer Nature, 422. doi: https://doi.org/10.1007/978-3-030-96603-4
  5. Yaroshevich, N., Puts, V., Yaroshevich, Т., Herasymchuk, O. (2020). Slow oscillations in systems with inertial vibration exciters. Vibroengineering PROCEDIA, 32, 20–25. doi: https://doi.org/10.21595/vp.2020.21509
  6. Samantaray, A. (2021). Efficiency considerations for Sommerfeld effect attenuation. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 235 (21), 5247–5260. doi: https://doi.org/10.1177/0954406221991584
  7. Lanets, O. V., Shpak, Ya. V., Lozynskyi, V. I., Leonovych, P. Yu. (2013). Realizatsiia efektu Zommerfelda u vibratsiinomu maidanchyku z inertsiinym pryvodom. Avtomatyzatsiia vyrobnychykh protsesiv u mashynobuduvanni ta pryladobuduvanni, 47, 12–28. Available at: http://nbuv.gov.ua/UJRN/Avtomatyzac_2013_47_4
  8. Kuzo, І. V., Lanetc, O. V., Gurskii, V. M. (2013). Synthesis of low-frequency resonance vibratory machines with an aeroinertia drive. Naukovyi visnyk Natsionalnoho hirnychoho universytetu, 2, 60–67. Available at: http://nbuv.gov.ua/UJRN/Nvngu_2013_2_11
  9. Ryzhik, B., Sperling, L., Duckstein, H. (2004). Non-synchronous Motions Near Critical Speeds in a Single-plane Autobalancing Device. Technische Mechanik, 24, 25–36. Available at: https://journals.ub.uni-magdeburg.de/index.php/techmech/article/view/911
  10. Lu, C.-J., Tien, M.-H. (2012). Pure-rotary periodic motions of a planar two-ball auto-balancer system. Mechanical Systems and Signal Processing, 32, 251–268. doi: https://doi.org/10.1016/j.ymssp.2012.06.001
  11. Jung, D. (2018). Supercritical Coexistence Behavior of Coupled Oscillating Planar Eccentric Rotor/Autobalancer System. Shock and Vibration, 2018, 1–19. doi: https://doi.org/10.1155/2018/4083897
  12. Drozdetskaya, O., Fidlin, A. (2021). Passing through resonance of the unbalanced rotor with self-balancing device. Nonlinear Dynamics, 106 (3), 1647–1657. doi: https://doi.org/10.1007/s11071-021-06973-4
  13. Artyunin, A. I., Eliseyev, S. V. (2013). Effect of “Crawling” and Peculiarities of Motion of a Rotor with Pendular Self-Balancers. Applied Mechanics and Materials, 373-375, 38–42. doi: https://doi.org/10.4028/www.scientific.net/amm.373-375.38
  14. Artyunin, A. I., Barsukov, S. V., Sumenkov, O. Y.; Radionov, A., Kravchenko, O., Guzeev, V., Rozhdestvenskiy, Y. (Eds.) (2020). Peculiarities of Motion of Pendulum on Mechanical System Engine Rotating Shaft. Proceedings of the 5th International Conference on Industrial Engineering (ICIE 2019). ICIE 2019. Lecture Notes in Mechanical Engineering. Cham: Springer, 649–657. doi: https://doi.org/10.1007/978-3-030-22041-9_70
  15. Filimonikhin, G., Yatsun, V. (2015). Method of excitation of dual frequency vibrations by passive autobalancers. Eastern-European Journal of Enterprise Technologies, 4 (7 (76)), 9–14. doi: https://doi.org/10.15587/1729-4061.2015.47116
  16. Filimonikhin, G., Yatsun, V., Filimonikhina, I., Ienina, I., Munshtukov, I. (2019). Studying the load jam modes within the framework of a flat model of the rotor with an auto­balancer. Eastern-European Journal of Enterprise Technologies, 5 (7 (101)), 51–61. doi: https://doi.org/10.15587/1729-4061.2019.177418
  17. Yatsun, V., Filimonikhin, G., Podoprygora, N., Pirogov, V. (2019). Studying the excitation of resonance oscillations in a rotor on isotropic supports by a pendulum, a ball, a roller. Eastern-European Journal of Enterprise Technologies, 6 (7 (102)), 32–43. doi: https://doi.org/10.15587/1729-4061.2019.182995
  18. Varanis, M., Balthazar, J. M., Silva, A., Mereles, A. G., Pederiva, R. (2018). Remarks on the Sommerfeld effect characterization in the wavelet domain. Journal of Vibration and Control, 25 (1), 98–108. doi: https://doi.org/10.1177/1077546318771804
  19. Yatsun, V., Filimonikhin, G., Nevdakha, A., Pirogov, V. (2018). Experimental study into rotational-oscillatory vibrations of a vibration machine platform excited by the ball auto-balancer. Eastern-European Journal of Enterprise Technologies, 4 (7 (94)), 34–42. doi: https://doi.org/10.15587/1729-4061.2018.140006
Determining experimentally the patterns of the manifestation of the Sommerfeld effect in a ball auto-balancer

Downloads

Published

2022-10-31

How to Cite

Filimonikhin, G., Yatsun, V., Matsui, A., Olijnichenko, L., & Pukalov, V. (2022). Determining experimentally the patterns of the manifestation of the Sommerfeld effect in a ball auto-balancer. Eastern-European Journal of Enterprise Technologies, 5(7 (119), 96–104. https://doi.org/10.15587/1729-4061.2022.265578

Issue

Vol. 5 No. 7 (119) (2022): Applied mechanics

Section

Applied mechanics

License

Copyright (c) 2022 Gennadiy Filimonikhin, Volodymyr Yatsun, Anatolii Matsui, Lubov Olijnichenko, Viktor Pukalov

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.

A license agreement is a document in which the author warrants that he/she owns all copyright for the work (manuscript, article, etc.).
The authors, signing the License Agreement with TECHNOLOGY CENTER PC, have all rights to the further use of their work, provided that they link to our edition in which the work was published.
According to the terms of the License Agreement, the Publisher TECHNOLOGY CENTER PC does not take away your copyrights and receives permission from the authors to use and dissemination of the publication through the world's scientific resources (own electronic resources, scientometric databases, repositories, libraries, etc.).
In the absence of a signed License Agreement or in the absence of this agreement of identifiers allowing to identify the identity of the author, the editors have no right to work with the manuscript.
It is important to remember that there is another type of agreement between authors and publishers – when copyright is transferred from the authors to the publisher. In this case, the authors lose ownership of their work and may not use it in any way.