Estimating the stability of steady motion of vibration machines operating on the somerfeld effect using an empirical method
DOI:
https://doi.org/10.15587/1729-4061.2022.268718Keywords:
inertial vibration exciter, resonant vibration machine, steady state mode of motion, Sommerfeld effect, stability of motionAbstract
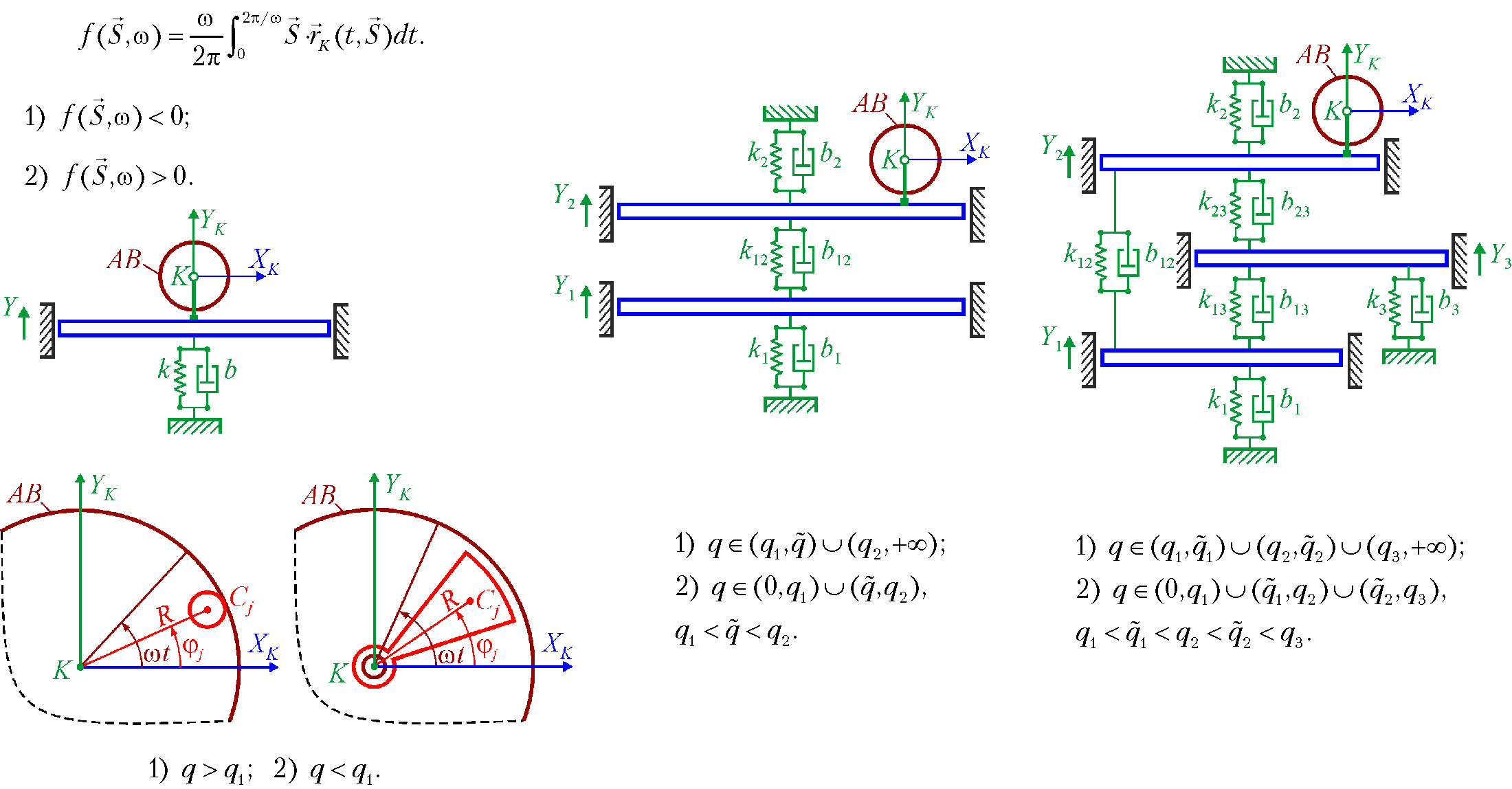
One-, two-, and three-mass vibration machines with translational motion of platforms and a vibration exciter of a ball, roller, or pendulum type with several loads were studied. The empirical criterion for the onset of auto-balancing was applied in the extended formulation.
It has been established that a single-mass vibration machine has one resonant speed, and:
– at the after-resonance speeds of rotation of loads synchronously with the rotor, the auto-balancing mode becomes stable;
– at the pre-resonance speeds of rotation of loads, loads tend to gather together.
In a dual-mass vibration machine, there are two resonant speeds and one additional speed located between two resonant ones. The auto-balancing mode is stable when the loads rotate synchronously with the rotor at the following speeds:
– between the first resonant speed and the additional speed;
– greater than the second resonant speed.
At other speeds of rotation of loads, loads tend to gather together.
The three-mass vibration machine has three resonant speeds and two additional speeds, located one by one between adjacent resonant speeds. The auto-balancing mode is stable when the loads rotate synchronously with the rotor at the following speeds:
– between the first resonant speed and the first additional speed;
– between the second resonant speed and the second additional speed;
– greater than the third resonant speed.
At other speeds of rotation of loads, loads tend to gather together.
In a single-mass vibration machine, the value of the resonant speed does not depend on the viscosity of supports. In dual-mass and three-mass vibration machines, all characteristic speeds depend on the viscosity of supports. With small forces of viscous resistance, the values of these speeds are close to the characteristic speeds found in the absence of resistance forces.
References
- Thearle, E. L. (1950). Automatic dynamic balancers (Part 2 – Ring, pendulum, ball balancers). Machine Design, 22 (10), 103–106.
- Sommerfeld, A. (1902). Beiträge zum dynamischen Ausbau der Festigkeitslehre. Zeitschrift des Vereines Deutscher Ingenieure, 46, 391–394.
- Ryzhik, B., Sperling, L., Duckstein, H. (2004). Non-Synchronous Motions Near Critical Speeds in a Single-Plane Auto-Balancing Device. Technische Mechanik, 24 (1), 25–36. Available at: https://journals.ub.uni-magdeburg.de/index.php/techmech/article/view/911
- Lu, C.-J., Tien, M.-H. (2012). Pure-rotary periodic motions of a planar two-ball auto-balancer system. Mechanical Systems and Signal Processing, 32, 251–268. doi: https://doi.org/10.1016/j.ymssp.2012.06.001
- Jung, D. (2018). Supercritical Coexistence Behavior of Coupled Oscillating Planar Eccentric Rotor/Autobalancer System. Shock and Vibration, 2018, 1–19. doi: https://doi.org/10.1155/2018/4083897
- Drozdetskaya, O., Fidlin, A. (2021). Passing through resonance of the unbalanced rotor with self-balancing device. Nonlinear Dynamics, 106 (3), 1647–1657. doi: https://doi.org/10.1007/s11071-021-06973-4
- Yatsun, V., Filimonikhin, G., Dumenko, K., Nevdakha, A. (2017). Equations of motion of vibration machines with a translational motion of platforms and a vibration exciter in the form of a passive auto-balancer. Eastern-European Journal of Enterprise Technologies, 5 (1 (89)), 19–25. doi: https://doi.org/10.15587/1729-4061.2017.111216
- Kuzo, I. V., Lanets, O. V., Gurskyi, V. M. (2013). Synthesis of low-frequency resonance vibratory machines with an aeroinertia drive. Naukovyi visnyk Natsionalnoho hirnychoho universytetu, 2, 60–67. Available at: http://nbuv.gov.ua/UJRN/Nvngu_2013_2_11
- Tusset, A. M., Bueno, Á. M., dos Santos, J. P. M., Tsuchida, M., Balthazar, J. M. (2016). A non-ideally excited pendulum controlled by SDRE technique. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 38 (8), 2459–2472. doi: https://doi.org/10.1007/s40430-016-0517-7
- Blekhman, I. I., Semenov, Yu. A., Yaroshevych, M. P. (2020). On the Possibility of Designing Adaptive Vibration Machinery Using Self-synchronizing Exciters. Mechanisms and Machine Science, 231–236. doi: https://doi.org/10.1007/978-3-030-33491-8_28
- Sperling, L., Ryzhik, B., Duckstein, H. (2004). Single-Plain Auto-Balancing of Rigid Rotors. Technische Mechanik, 24 (1).
- Yaroshevich, N., Puts, V., Yaroshevich, Т., Herasymchuk, O. (2020). Slow oscillations in systems with inertial vibration exciters. Vibroengineering PROCEDIA, 32, 20–25. doi: https://doi.org/10.21595/vp.2020.21509
- Sohn, J.-S., Lee, J. W., Cho, E.-H., Park, N.-C., Park, Y.-P. (2007). Dynamic Analysis of a Pendulum Dynamic Automatic Balancer. Shock and Vibration, 14 (2), 151–167. doi: https://doi.org/10.1155/2007/452357
- Filimonikhin, G., Filimonikhina, I., Dumenko, K., Lichuk, M. (2016). Empirical criterion for the occurrence of auto-balancing and its application for axisymmetric rotor with a fixed point and isotropic elastic support. Eastern-European Journal of Enterprise Technologies, 5 (7 (83)), 11–18. doi: https://doi.org/10.15587/1729-4061.2016.79970
- Filimonikhin, G., Filimonikhina, I., Yakymenko, M., Yakimenko, S. (2017). Application of the empirical criterion for the occurrence of auto-balancing for axisymmetric rotor on two isotropic elastic supports. Eastern-European Journal of Enterprise Technologies, 2 (7 (86)), 51–58. doi: https://doi.org/10.15587/1729-4061.2017.96622
Downloads
Published
How to Cite
Issue
Section
License
Copyright (c) 2022 Gennadiy Filimonikhin, Volodymyr Amosov, Antonina Haleeva, Iryna Ienina, Mareks Mezitis, Yuriy Nevdakha, Guntis Strautmanis, Oleksii Vasylkovskyi

This work is licensed under a Creative Commons Attribution 4.0 International License.
The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.
A license agreement is a document in which the author warrants that he/she owns all copyright for the work (manuscript, article, etc.).
The authors, signing the License Agreement with TECHNOLOGY CENTER PC, have all rights to the further use of their work, provided that they link to our edition in which the work was published.
According to the terms of the License Agreement, the Publisher TECHNOLOGY CENTER PC does not take away your copyrights and receives permission from the authors to use and dissemination of the publication through the world's scientific resources (own electronic resources, scientometric databases, repositories, libraries, etc.).
In the absence of a signed License Agreement or in the absence of this agreement of identifiers allowing to identify the identity of the author, the editors have no right to work with the manuscript.
It is important to remember that there is another type of agreement between authors and publishers – when copyright is transferred from the authors to the publisher. In this case, the authors lose ownership of their work and may not use it in any way.









