Automatic construction of a fuzzy system with a matrix representation of rules and a correct knowledge base

Authors

DOI:

https://doi.org/10.15587/1729-4061.2022.268908

Keywords:

expert system, fuzzy logic, fuzzy classification, Hoare logic, resolution method

Abstract

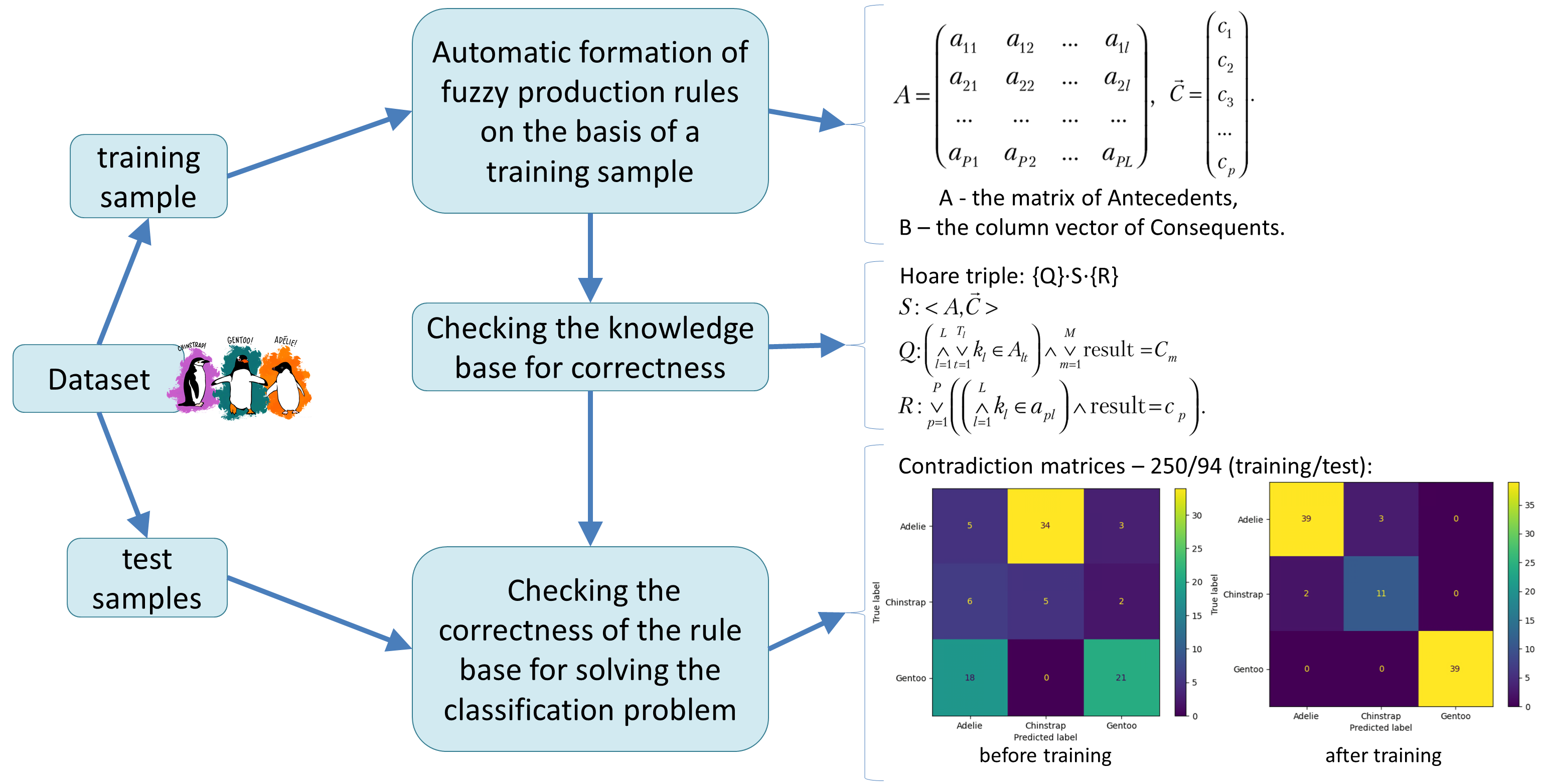
The object of this study is the process of automatic formation of fuzzy production rules on the basis of a training sample for solving the classification problem. The problem of automatically creating and then checking the correctness of a fuzzy inference model for a classification task is solved. The result is an automatically constructed correct database of rules for solving the classification problem. Analysis of the correctness of the knowledge base is carried out using the criteria of completeness, minimality, coherence, and consistency. To prove the completeness of the rule base, Hoare logic and the resolution method are used. The quality of the classification is assessed using such metrics as accuracy, precision, recall, f1-score. The dependence of the classification result on the size of the training sample is considered.

The expert system has the following features: the ability to learn from data; high level of accuracy; the correct knowledge base. The knowledge base is formed using the objects of the training sample on the basis of linguistic variables and term sets. A production model of knowledge representation is applied, combining the Mamdani and Takagi-Sugeno-Kang models. It is assumed that the left parts of the production rules describe combinations of the features of objects, and the right parts correspond to classes. The matrix representation of the antecedents of the rules is used. Consequents are represented as a column vector. For the automatic construction of the matrix of antecedents, it is proposed to use the Cartesian product. The formation of the consequent vector is carried out automatically using domain data and a training procedure.

The resulting expert system can be used to solve the problems of classification, clustering, data mining, and big data analysis

Author Biographies

Danylo Yehoshkin, Oles Honchar Dnipro National University

Postgraduate Student

Department of Computer Technology

Natalia Guk, Oles Honchar Dnipro National University

Doctor of Physical and Mathematical Sciences, Professor, Head of Department

Department of Computer Technology

References

  1. Zadeh, L. A., Abbasov, A. M., Yager, R. R., Shahbazova, S. N., Reformat, M. Z. (Eds.) (2014). Recent Developments and New Directions in Soft Computing. Studies in Fuzziness and Soft Computing. doi: https://doi.org/10.1007/978-3-319-06323-2
  2. Ternovoi, M. Yu., Shtohryna, E. S. (2015). Formalnaia spetsyfykatsyia svoistv baz nechetkykh znanyi Mamdany na osnove metahrafa. Visnyk Kharkivskoho natsionalnoho universytetu imeni V. N. Karazina. Seriya: Matematychne modeliuvannia. Informatsiyni tekhnolohiyi. Avtomatyzovani systemy upravlinnia, 27, 157–171. Available at: http://nbuv.gov.ua/UJRN/VKhIMAM_2015_27_17
  3. Krivulya, G. F., Shkil', A. S., Kucherenko, D. E. (2013). Analiz korrektnosti produkcionnyh pravil v sistemah nechetkogo logicheskogo vyvoda s ispol'zovaniem kvantovyh modelej. ASU i pribory avtomatiki, 165, 42–53. Available at: https://openarchive.nure.ua/server/api/core/bitstreams/eeb5b66f-7eb9-4db4-b045-0e774308ee6d/content
  4. Darwiche, A., Marquis, P. (2002). A Knowledge Compilation Map. Journal of Artificial Intelligence Research, 17, 229–264. doi: https://doi.org/10.1613/jair.989
  5. Sugiura, A., Riesenhuber, M., Koseki, Y. (1993). Comprehensibility Improvement of Tabular Knowledge Bases. AAAI-93 Proceedings, 716–721. Available at: https://www.aaai.org/Papers/AAAI/1993/AAAI93-107.pdf
  6. Sugiura, A., Koseki, Y. (1995). Comprehensibility Improvement of Tabular Knowledge Bases. Journal of the Japanese Society for Artificial Intelligence, 10 (4), 628–635. doi: https://doi.org/10.11517/jjsai.10.4_628
  7. Kondratenko, Y. P., Kozlov, A. V. (2019). Generation of Rule Bases of Fuzzy Systems Based on Modified Ant Colony Algorithms. Journal of Automation and Information Sciences, 51 (3), 4–25. doi: https://doi.org/10.1615/jautomatinfscien.v51.i3.20
  8. Zheldak, T. A., Koriashkina, L. S. (2020). Nechitki mnozhyny v systemakh upravlinnia ta pryiniattia rishen. Dnipro: NTU «DP», 222–227.
  9. Hoare, C. A. R. (1969). An axiomatic basis for computer programming. Communications of the ACM, 12 (10), 576–580. doi: https://doi.org/10.1145/363235.363259
  10. Gries, D. (1981). The Predicate Transformer wp. The Science of Programming, 108–113. doi: https://doi.org/10.1007/978-1-4612-5983-1_8
  11. Dijkstra, E. W. (1975). Guarded commands, nondeterminacy and formal derivation of programs. Communications of the ACM, 18 (8), 453–457. doi: https://doi.org/10.1145/360933.360975
  12. Simplify. ESC/Java2 Summary. Available at: https://www.kindsoftware.com/products/opensource/escjava2
  13. Hizha, A. L., Vysokopoyasnyj, I. G. (2017). Avtomaticheskaya proverka semanticheskoy pravil'nosti resheniy zadach po programmirovaniyu. Pytannia prykladnoi matematyky i matematychnoho modeliuvannia, 17, 234–246. Available at: http://nbuv.gov.ua/UJRN/Ppmmm_2017_17_29
  14. Gorman, K. B., Williams, T. D., Fraser, W. R. (2014). Ecological Sexual Dimorphism and Environmental Variability within a Community of Antarctic Penguins (Genus Pygoscelis). PLoS ONE, 9 (3), e90081. doi: https://doi.org/10.1371/journal.pone.0090081
Automatic construction of a fuzzy system with a matrix representation of rules and a correct knowledge base

Downloads

Published

2022-12-30

How to Cite

Yehoshkin, D., & Guk, N. (2022). Automatic construction of a fuzzy system with a matrix representation of rules and a correct knowledge base . Eastern-European Journal of Enterprise Technologies, 6(4 (120), 14–22. https://doi.org/10.15587/1729-4061.2022.268908

Issue

Vol. 6 No. 4 (120) (2022): Mathematics and Cybernetics - applied aspects

Section

Mathematics and Cybernetics - applied aspects

License

Copyright (c) 2022 Danylo Yehoshkin, Natalia Guk

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.

A license agreement is a document in which the author warrants that he/she owns all copyright for the work (manuscript, article, etc.).
The authors, signing the License Agreement with TECHNOLOGY CENTER PC, have all rights to the further use of their work, provided that they link to our edition in which the work was published.
According to the terms of the License Agreement, the Publisher TECHNOLOGY CENTER PC does not take away your copyrights and receives permission from the authors to use and dissemination of the publication through the world's scientific resources (own electronic resources, scientometric databases, repositories, libraries, etc.).
In the absence of a signed License Agreement or in the absence of this agreement of identifiers allowing to identify the identity of the author, the editors have no right to work with the manuscript.
It is important to remember that there is another type of agreement between authors and publishers – when copyright is transferred from the authors to the publisher. In this case, the authors lose ownership of their work and may not use it in any way.