Determining static characteristics of corrugated shell elements made from composite materials
DOI:
https://doi.org/10.15587/1729-4061.2022.269399Keywords:
corrugated shell membrane, elastic static characteristic, composite materials, mechanical characteristics of reinforced shellsAbstract
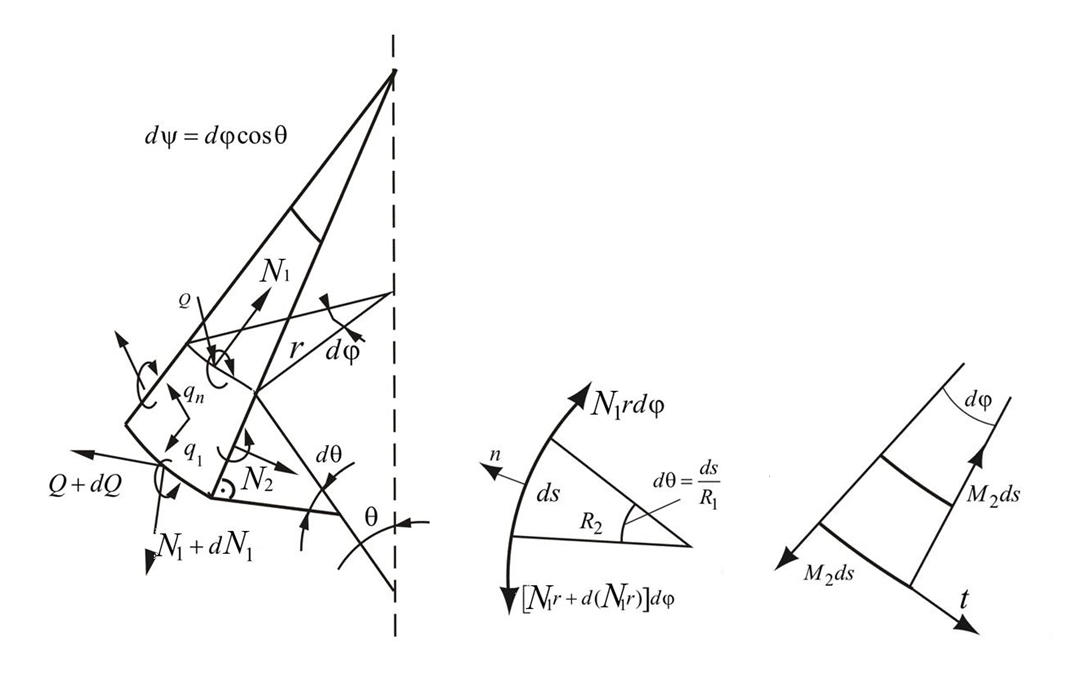
This paper considers elastic shell elements. They move under pressure. The type of dependence of displacement on pressure is called the elastic characteristic of the element. The object of this study is shell elements with a complex surface shape, consisting of composite materials of the "metal-metal" type. The composite is a metal shell with reinforcing fiber made of another metal material. The form of reinforcement is different. The task to be solved is to determine the elastic characteristics of the shell elements depending on the geometric parameters, as well as the mechanical values of the shell at its various points and in different directions. To this end, algorithms were built for calculating mechanical quantities depending on the percentage of the fiber and the shell matrix. It was required to derive a system of equations for determining the displacements and internal forces in the element depending on the geometric and mechanical parameters. A numerical calculation of shell elastic elements was performed and a comparison of the results of analytical calculation according to the algorithm developed in this work and experimental data was performed. The match between these results is 99.8–100 %. The characteristics of the shell elements were determined depending on the type of reinforcing fiber and matrix, on the geometric parameters, and the type of reinforcement of the shell. These studies make it possible to design shell elements with specified characteristics and predefined sensitivity.
References
- Andreeva, L. E. (1962). Uprugie elementy priborov. Moscow: Mashgiz, 456.
- Alfutov, N. A., Zinov'ev, P. A., Popov, B. G. (1984). Raschet mnogosloynyh plastin i obolochek iz kompozitsionnyh materialov. Moscow: Mashinostroenie, 264.
- Shimyrbaev, M. K. (1992). Utochnennye metody opredeleniya uprugih postoyannyh odnonapravlenno armirovannogo materiala. Vestnik AN RK.
- Kurochka, K. S., Nesterenya, I. L. (2014). Raschet mnogosloynyh osesimmetrichnyh obolochek metodom konechnyh elementov. Informatsionnye tekhnologii i sistemy 2014 (ITS 2014): materialy mezhdunarodnoy nauchnoy konferentsii. Minsk, 214–215. Available at: https://libeldoc.bsuir.by/handle/123456789/2008
- Golova, T. A., Andreeva, N. V. (2019). Analysis of methods of calculation of layered plates and shells for the calculation of multilayer structures. The Eurasian Scientific Journal, 5 (11).
- Bazhenov, V. A., Solovei, N. A., Krivenko, O. P., Mishchenko, O. A. (2014). Modeling of nonlinear deformation and buckling of elastic inhomogeneities shells. Stroitel'naya mekhanika inzhenernyh konstruktsiy i sooruzheniy, 5, 14–33.
- Kairov A. S., Vlasov O. I., Latanskaya L. A. (2017). Free vibrations of constructional non-homogeneous multilayer orthotropic composite cylindrical shells. Visnik Zaporizʹkogo nacionalʹnogo universitetu. Fiziko-matematicni nauki, 2, 57–65.
- San’kov, P., Tkach, N., Voziian, K., Lukianenko, V. (2016). Composite building materials and products. International scientific journal, 4 (1), 80–82. Available at: http://nbuv.gov.ua/UJRN/mnj_2016_4(1)__24
- Yankovskii, A. P. (2020). The refined model of viscoelastic-plastic deformation of reinforced cylindrical shells. PNRPU Mechanics Bulletin, 1, 138–149. doi: https://doi.org/10.15593/perm.mech/2020.1.11
- Bakulin, V. N. (2019). Posloyniy analiz napryazhenno-deformirovannogo sostoyaniya trekhsloynyh obolochek s vyrezami. Izvestiya Rossiyskoy Akademii Nauk. Mekhanika Tverdogo Tela, 2, 111–125. doi: https://doi.org/10.1134/s0572329919020028
- Senjanović, I., Čakmak, D., Alujević, N., Ćatipović, I., Vladimir, N., Cho, D.-S. (2019). Pressure and rotation induced tensional forces of toroidal shell and their influence on natural vibrations. Mechanics Research Communications, 96, 1–6. doi: https://doi.org/10.1016/j.mechrescom.2019.02.003
- Polyakova, I., Imambayeva, R., Aubakirova, B. (2021). Determining the dynamic characteristics of elastic shell structures. Eastern-European Journal of Enterprise Technologies, 6 (7 (114)), 43–51. doi: https://doi.org/10.15587/1729-4061.2021.245885
- Abramczyk, J. (2021). Transformed Shell Structures Determined by Regular Networks as a Complex Material for Roofing. Materials, 14 (13), 3582. doi: https://doi.org/10.3390/ma14133582
- Treshchev, A., Lapshina, M., Zavyalova, Y. (2021). Thermomechanical deformation of the orthotropic shell taking into account the deformation anisotropy. E3S Web of Conferences, 274, 03026. doi: https://doi.org/10.1051/e3sconf/202127403026
- Myntiuk, V. (2021). Spectral solution to a problem on the axisymmetric nonlinear deformation of a cylindrical membrane shell due to pressure and edges convergence. Eastern-European Journal of Enterprise Technologies, 5 (7 (113)), 6–13. doi: https://doi.org/10.15587/1729-4061.2021.242372
- Liu, Y., Zhu, R., Qin, Z., Chu, F. (2022). A comprehensive study on vibration characteristics of corrugated cylindrical shells with arbitrary boundary conditions. Engineering Structures, 269, 114818. doi: https://doi.org/10.1016/j.engstruct.2022.114818
- Lai, M., Eugster, S. R., Reccia, E., Spagnuolo, M., Cazzani, A. (2022). Corrugated shells: An algorithm for generating double-curvature geometric surfaces for structural analysis. Thin-Walled Structures, 173, 109019. doi: https://doi.org/10.1016/j.tws.2022.109019
- Khurukijwanich, C., Aimmanee, S. (2021). Anisotropic behaviors of helically corrugated cylindrical shells: Homogenized in-plane stiffness. Thin-Walled Structures, 160, 107378. doi: https://doi.org/10.1016/j.tws.2020.107378
- Khurukijwanich, C., Aimmanee, S. (2021). Anisotropic behaviors of helically corrugated cylindrical shells: Stress distributions and edge effects. Thin-Walled Structures, 168, 108263. doi: https://doi.org/10.1016/j.tws.2021.108263
- Biderman, V. L. (1977). Mekhanika tonkostennyh konstruktsiy. Moscow: Mashinostroenie, 488.
Downloads
Published
How to Cite
Issue
Section
License
Copyright (c) 2022 Irina Polyakova, Raikhan Imambayeva, Bakyt Aubakirova, Nazym Shogelova, Yevgeniya Glyzno, Aigerim Zhumagulova

This work is licensed under a Creative Commons Attribution 4.0 International License.
The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.
A license agreement is a document in which the author warrants that he/she owns all copyright for the work (manuscript, article, etc.).
The authors, signing the License Agreement with TECHNOLOGY CENTER PC, have all rights to the further use of their work, provided that they link to our edition in which the work was published.
According to the terms of the License Agreement, the Publisher TECHNOLOGY CENTER PC does not take away your copyrights and receives permission from the authors to use and dissemination of the publication through the world's scientific resources (own electronic resources, scientometric databases, repositories, libraries, etc.).
In the absence of a signed License Agreement or in the absence of this agreement of identifiers allowing to identify the identity of the author, the editors have no right to work with the manuscript.
It is important to remember that there is another type of agreement between authors and publishers – when copyright is transferred from the authors to the publisher. In this case, the authors lose ownership of their work and may not use it in any way.









