Implementing the method of figurative transformations to minimize partially defined Boolean functions

Authors

DOI:

https://doi.org/10.15587/1729-4061.2023.273293

Keywords:

minimization of partially defined Boolean functions by the method of figurative transformations, location of equivalent transformations

Abstract

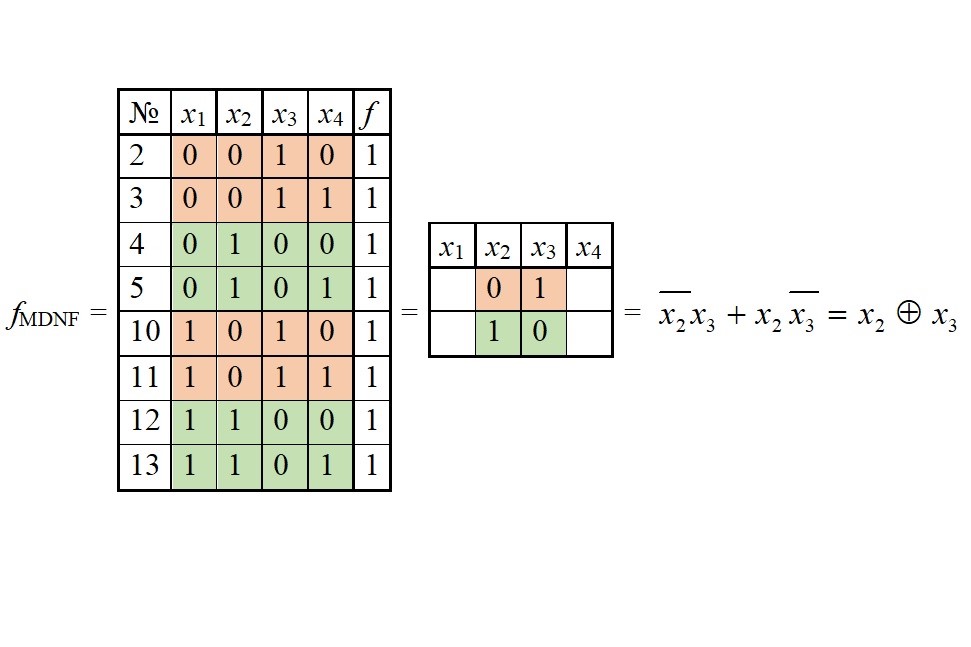
This paper reports a research that established the possibility of increasing the effectiveness of the method of figurative transformations to minimize partially defined Boolean functions. The method makes it possible, without loss of functionality, to reduce the complexity of the minimization procedure, compared to sorting out binary definitions of partially defined Boolean functions. The interpretation of the result is that the 2-(n, b)-design, 2-(n, x/b)-design systems are a reflection of logical operations. Therefore, the identification of such combinatorial systems in the truth table of logical functions directly and unambiguously establishes the location of logical operations for equivalent transformations of Boolean expressions. This, in turn, implicates an algorithm for simplifying Boolean functions, including partially defined Boolean functions. Thus, the method of figurative transformations simplifies and speeds up the procedure for minimizing partially defined Boolean functions, compared to analogs. This indicates that the visual-matrix form of the analytical method still has the prospect of increasing its hardware capabilities, including in terms of minimizing partially defined Boolean functions.

It has been experimentally confirmed that the method of figurative transformations increases the efficiency of minimizing partially defined Boolean functions, compared with analogs, by 100–200 %.

There is reason to argue about the possibility of increasing the efficiency of minimizing partially defined Boolean functions in the main and polynomial bases by the specified method. The effectiveness of the method, in particular, is ensured by carrying out all operations of generalized gluing of variables for dead-end disjunctive normal forms (DNF), followed by the use of implicant tables; optimal combination of a sequence of logical operations for gluing variables

Author Biographies

Mykhailo Solomko, National University of Water and Environmental Engineering

PhD, Associate Professor

Department of Computer Engineering

Mykola Antoniuk, Rivne State University of Humanities

PhD, Associate Professor

Department of Information and Communication Technologies and Methods of Teaching Informatics

Ihor Voitovych, Rivne State University of Humanities

Doctor of Pedagogical Sciences, Professor

Department of Information and Communication Technologies and Methods of Teaching Informatics

Yuliia Ulianovska, University of Customs and Finance

PhD, Associate Professor

Department of Computer Science and Software Engineering

Nataliia Pavlova, Rivne State University of Humanities

PhD, Associate Professor

Department of Information and Communication Technologies and Methods of Teaching Computer Science

Viacheslav Biletskyi, Rivne State University of Humanities

PhD, Associate Professor

Department of Information and Communication Technologies and Methods of Teaching Computer Science

References

  1. Savel'ev, A. Ya. (1987). Prikladnaya teoriya cifrovyh avtomatov. Moscow: Vysshaya shkola, 272. Available at: https://vdoc.pub/documents/-4o35jbu52gg0
  2. Prihozhiy, A. A. (2013). Chastichno opredelyonnye logicheskie sistemy i algoritmy. Minsk: BNTU, 343. Available at: https://rep.bntu.by/handle/data/37237
  3. Papakonstantinou, K. G., Papakonstantinou, G. (2018). A Nonlinear Integer Programming Approach for the Minimization of Boolean Expressions. Journal of Circuits, Systems and Computers, 27 (10), 1850163. doi: https://doi.org/10.1142/s0218126618501633
  4. Fišer, P., Hlavičcka, J. (2000). Efficient minimization method for Incompletely defined Boolean functions. Conference: 4th Int. Workshop on Boolean Problems (IWSBP). Available at: https://www.researchgate.net/publication/260987269_Efficient_minimization_method_for_incompletely_defined_Boolean_functions
  5. Dimopoulos, A. C., Pavlatos, C., Papakonstantinou, G. (2022). Multi‐output, multi‐level, multi‐gate design using non‐linear programming. International Journal of Circuit Theory and Applications, 50 (8), 2960–2968. doi: https://doi.org/10.1002/cta.3300
  6. Scholl, C., Melchior, S., Hotz, G., Molitor, P. (1997). Minimizing ROBDD sizes of incompletely specified Boolean functions by exploiting strong symmetries. Proceedings European Design and Test Conference. ED & TC 97. doi: https://doi.org/10.1109/edtc.1997.582364
  7. Rytsar, B. (2015). The Minimization Method of Boolean Functions in Polynomial Set-theoretical Format. Conference: Proc. 24th Inter. Workshop, CS@P’2015. Rzeszow, 130–146. Available at: https://www.researchgate.net/publication/298158364_The_Minimization_Method_of_Boolean_Functionns_in_Polynomial_Set-theoretical_Format
  8. Costamagna, A., De Micheli, G. (2023). Accuracy recovery: A decomposition procedure for the synthesis of partially-specified Boolean functions. Integration, 89, 248–260. doi: https://doi.org/10.1016/j.vlsi.2022.12.008
  9. Boroumand, S., Bouganis, C.-S., Constantinides, G. A. (2021). Learning Boolean Circuits from Examples for Approximate Logic Synthesis. Proceedings of the 26th Asia and South Pacific Design Automation Conference. doi: https://doi.org/10.1145/3394885.3431559
  10. Solomko, M. (2021). Developing an algorithm to minimize boolean functions for the visual-matrix form of the analytical method. Eastern-European Journal of Enterprise Technologies, 1 (4 (109)), 6–21. doi: https://doi.org/10.15587/1729-4061.2021.225325
  11. Riznyk, V., Solomko, M., Tadeyev, P., Nazaruk, V., Zubyk, L., Voloshyn, V. (2020). The algorithm for minimizing Boolean functions using a method of the optimal combination of the sequence of figurative transformations. Eastern-European Journal of Enterprise Technologies, 3 (4 (105)), 43–60. doi: https://doi.org/10.15587/1729-4061.2020.206308
  12. Minimizatsiya nepovnistiu vyznachenykh lohichnykh funktsiy. Available at: https://studfile.net/preview/14499737/page:17/
  13. Riznyk, V., Solomko, M. (2017). Application of super-sticking algebraic operation of variables for Boolean functions minimization by combinatorial method. Technology Audit and Production Reserves, 6 (2 (38)), 60–76. doi: https://doi.org/10.15587/2312-8372.2017.118336
  14. Pottosin, Yu. V. (2021). Minimization of Boolean functions in the class of orthogonal disjunctive normal forms. Informatics, 18 (2), 33–47. doi: https://doi.org/10.37661/1816-0301-2021-18-2-33-47
  15. Zakrevskij, A. D., Toropov, N. R., Romanov, V. I. (2010). DNF-implementation of partial boolean functions of many variables. Informatics, 1 (25), 102–111. Available at: https://inf.grid.by/jour/article/view/461/419
  16. Solomko, M., Batyshkina, I., Khomiuk, N., Ivashchuk, Y., Shevtsova, N. (2021). Developing the minimization of a polynomial normal form of boolean functions by the method of figurative transformations. Eastern-European Journal of Enterprise Technologies, 2 (4 (110)), 22–37. doi: https://doi.org/10.15587/1729-4061.2021.229786
  17. Riznyk, V., Solomko, M. (2018). Minimization of conjunctive normal forms of boolean functions by combinatorial method. Technology Audit and Production Reserves, 5 (2 (43)), 42–55. doi: https://doi.org/10.15587/2312-8372.2018.146312
  18. Sdvizhkov, O. A. (2012). Diskretnaya matematika i matematicheskie metody ekonomiki s primeneniem VBA Ehcel. Moscow: DMK, 212. Available at: https://www.studmed.ru/sdvizhkov-o-a-diskretnaya-matematika-i-matematicheskie-metody-ekonomiki-s-primeneniem-vba-excel_9edfd48c895.html
  19. Huang, J. (2014). Programing implementation of the Quine-McCluskey method for minimization of Boolean expression. arXiv. doi: https://doi.org/10.48550/arXiv.1410.1059
  20. Matematychna lohika ta dyskretna matematyka (2020). Kremenchuk, 61. Available at: http://document.kdu.edu.ua/metod/2020_2182.pdf
  21. Novytskyi, I. V., Us, S. A. (2013). Dyskretna matematyka v prykladakh i zadachakh. Dnipropetrovsk, 89. Available at: https://sau.nmu.org.ua/ua/osvita/metod/Discrete_Math(Novitskiy_Us_NMU_SAU).pdf
  22. Rytsar, B. Ye. (2015). A New Method of Minimization of Logical Functions in the Polynomial Set-theoretical Format. 2. Minimization of Complete and Incomplete Functions. УСиМ, 4, 9–30. Available at: http://dspace.nbuv.gov.ua/handle/123456789/87235
  23. Solomko, M., Batyshkina, I., Voitovych, I., Zubyk, L., Babych, S., Muzychuk, K. (2020). Devising a method of figurative transformations for minimizing boolean functions in the implicative basis. Eastern-European Journal of Enterprise Technologies, 6 (4 (108)), 32–47. doi: https://doi.org/10.15587/1729-4061.2020.220094
  24. Solomko, M., Tadeyev, P., Zubyk, L., Babych, S., Mala, Y., Voitovych, O. (2021). Implementation of the method of figurative transformations to minimizing symmetric Boolean functions. Eastern-European Journal of Enterprise Technologies, 4 (4 (112)), 23–39. doi: https://doi.org/10.15587/1729-4061.2021.239149
  25. Zakrevskiy, A. D. (1981). Logicheskiy sintez kaskadnyh shem. Moscow, 414.
  26. Chu, Z., Pan, H. (2023). Survey on Exact Logic Synthesis Based on Boolean SATisfiability. Journal of Electronics & Information Technology, 45 (1), 14–23. doi: https://doi.org/10.11999/JEIT220391
  27. Yong-Xin, X. (1987). Xiao map for minimization of boolean expression. International Journal of Electronics, 63 (3), 353–358. doi: https://doi.org/10.1080/00207218708939138
  28. Osuagwu, C. C., Anyanwu, C. D., Agada, J. O. (1989). Fast Minimization on the Xiao Map Using Row Group Structure Rules. Nigerian Journal of Technology, 13 (1), 51–61. Available at: https://www.ajol.info/index.php/njt/article/view/123260
Implementing the method of figurative transformations to minimize partially defined Boolean functions

Downloads

Published

2023-02-28

How to Cite

Solomko, M., Antoniuk, M., Voitovych, I., Ulianovska, Y., Pavlova, N., & Biletskyi, V. (2023). Implementing the method of figurative transformations to minimize partially defined Boolean functions. Eastern-European Journal of Enterprise Technologies, 1(4 (121), 6–25. https://doi.org/10.15587/1729-4061.2023.273293

Issue

Vol. 1 No. 4 (121) (2023): Mathematics and Cybernetics - applied aspects

Section

Mathematics and Cybernetics - applied aspects

License

Copyright (c) 2023 Mykhailo Solomko, Mykola Antoniuk, Ihor Voitovych, Yuliia Ulianovska, Nataliia Pavlova, Viacheslav Biletskyi

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.

A license agreement is a document in which the author warrants that he/she owns all copyright for the work (manuscript, article, etc.).
The authors, signing the License Agreement with TECHNOLOGY CENTER PC, have all rights to the further use of their work, provided that they link to our edition in which the work was published.
According to the terms of the License Agreement, the Publisher TECHNOLOGY CENTER PC does not take away your copyrights and receives permission from the authors to use and dissemination of the publication through the world's scientific resources (own electronic resources, scientometric databases, repositories, libraries, etc.).
In the absence of a signed License Agreement or in the absence of this agreement of identifiers allowing to identify the identity of the author, the editors have no right to work with the manuscript.
It is important to remember that there is another type of agreement between authors and publishers – when copyright is transferred from the authors to the publisher. In this case, the authors lose ownership of their work and may not use it in any way.