Determining a flow structure in the region of local obstacles of different types taking into account the hydrodynamic conditions for entering the initial section

Authors

DOI:

https://doi.org/10.15587/1729-4061.2023.277342

Keywords:

local obstacles of various types, onditions for entering the initial section, numerical solution

Abstract

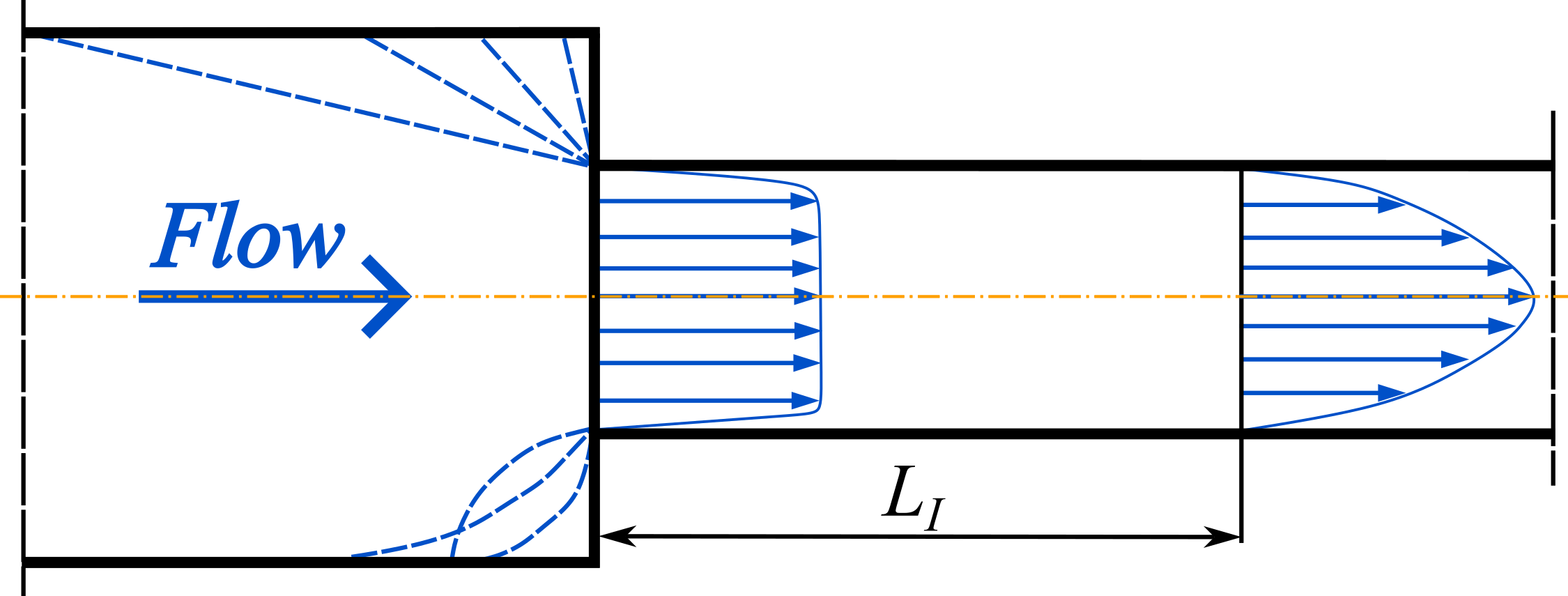
This paper investigates the influence of hydrodynamic conditions for entering the initial section of the channel located after local obstacles of various types. It is shown that the head losses in the valves and bends of pipelines and in various control elements can be several times higher than those in straight sections of the pipeline. It was established that the assumption about the rectangular shape of the velocity diagram at the entrance to the hydrodynamic initial section does not correspond to the flow pattern in real channels of technological equipment. It is proved that with the manifestation of inertia forces in the flow at the initial section of the channel, hydrodynamic energy losses usually increase, velocity and stress fields are significantly deformed. Given this, it seemed expedient to conduct a study into the processes of flow of viscous liquids in the initial section, located after local obstacles of various types. Experimental and analytical studies have confirmed that there is a significant influence of boundary conditions at the entrance to the initial section on the formation of velocity diagrams and energy loss along its length. The analytical-numerical solution to the system of differential equations describing such flow is given. While solving, the system of equations, by appropriate transformations, takes the form of a nonlinear integral-differential equation. This makes it possible to obtain correct dependences for determining the length of the velocity distribution and energy loss in the investigated section of the channel. The results of calculations of velocity fields in the region of local obstacles agree well with known ideas of the flow pattern, which is observed in physical experiments and the results of analytical solutions. The quantitative difference in results ranges within 12–20 % depending on the Reynolds number. Thus, there is reason to assert that the results of studies reported here could be the basis for devising a procedure of hydrodynamic calculation aimed at structural and operational improvement of existing and designed technological equipment.

Author Biographies

Serhii Nosko, National Technical University of Ukraine “Igor Sikorsky Kyiv Polytechnic Institute”

PhD, Associate Professor

Department of Applied Hydro-Aeromechanics and Mechatronics

Dmytro Kostiuk, National Technical University of Ukraine “Igor Sikorsky Kyiv Polytechnic Institute”

PhD, Senior Lecturer

Department of Applied Hydro-Aeromechanics and Mechatronics

Oleksandr Haletskyi, National Technical University of Ukraine “Igor Sikorsky Kyiv Polytechnic Institute”

PhD, Senior Lecturer

Department of Applied Hydro-Aeromechanics and Mechatronics

Ihor Nochnichenko, National Technical University of Ukraine “Igor Sikorsky Kyiv Polytechnic Institute”

PhD, Associate Professor

Department of Applied Hydro-Aeromechanics and Mechatronics

References

  1. Safarifard, M., Aghaee, Z., Pourjafar, M., Bazargan, S., Sadeghy, K. (2020). Hydroelastic instability of viscoelastic fluids in developing flow through a compliant channel. Korea-Australia Rheology Journal, 32 (2), 99–119. doi: https://doi.org/10.1007/s13367-020-0010-9
  2. Joshi, Y., Vinoth, B. R. (2018). Entry Lengths of Laminar Pipe and Channel Flows. Journal of Fluids Engineering, 140 (6). doi: https://doi.org/10.1115/1.4038668
  3. Bruyatskiy, E. V., Kostin, A. G. (2009). Raschet poley skorosti i davleniya dlya techeniya v ploskom kanale s vnezapnym odnostoronnim suzheniem. Prykladnaia hidromekhanika, 11 (2), 3–15. Available at: http://hydromech.org.ua/content/pdf/ph/ph-11-2(03-15).pdf
  4. Bruyatskiy, E. V., Kostin, A. G., Nikiforovich, E. I., Rozumnyuk, N. V. (2008). Metod chislennogo resheniya uravneniy Nav'e-Stoksa v peremennykh skorost'-davlenie. Prykladna hidromekhanika, 10 (2), 13–23. Available at: http://dspace.nbuv.gov.ua/bitstream/handle/123456789/4635/02-Brujatskiy.pdf?sequence=1
  5. Zargartalebi, A., Zargartalebi, M., Benneker, A. M. (2021). Analysis of vortices in viscoelastic fluid flow through confined geometries at low Reynolds numbers. AIP Advances, 11 (8), 085213. doi: https://doi.org/10.1063/5.0059041
  6. Everts, M., Meyer, J. P. (2020). Laminar hydrodynamic and thermal entrance lengths for simultaneously hydrodynamically and thermally developing forced and mixed convective flows in horizontal tubes. Experimental Thermal and Fluid Science, 118, 110153. doi: https://doi.org/10.1016/j.expthermflusci.2020.110153
  7. Kutuzov, A. G. (2012). Bezvikhrevoe techenie vuzkouprugoy zhidkosti vo vkhodnom kanale ekstruzionnoy golovki Vestnik KGTU, 2, 137–139.
  8. Verbeeten, W. M. H., Peters, G. W. M., Baaijens, F. P. T. (2001). Differential constitutive equations for polymer melts: The extended Pom–Pom model. Journal of Rheology, 45 (4), 823–843. doi: https://doi.org/10.1122/1.1380426
  9. Kutuzova, E. R., Tazyukov, F. Kh., Khalaf, Kh. A. (2014). Dinamika techeniya vyazkouprugoy zhidkosti cherez ploskoe 8:1 suzhenie. Vest. Kazansk. Tekhnologich, 2, 83–85.
  10. Nosko, S. V., Bulygin, V. A. (2012). Hydrodynamic calculation of the forming part of machine for processing of cellulose acetate. Eastern-European Journal of Enterprise Technologies, 2 (7 (56)), 48–52. Available at: http://journals.uran.ua/eejet/article/view/3758
  11. Nosko, S. V., Mosiychuk, V. A. (2011). Issledovanie kinematicheskikh kharakteristik potoka v kanalakh litnikovoy sistemy, metodami vizualizatsii. Vestnik NTUU «KPI»: Mashinostroenie, 62, 79–82.
  12. Hnativ, R. M. (2011). Vykorystannia dopplerivskoho lokatora dlia vymiriuvannia shvydkostei pry neustalenomu rusi ridyn. Promyslova hidravlika i pnevmatyka, 1 (31), 60–63. Available at: http://nbuv.gov.ua/UJRN/inhpn_2011_1_16
  13. Poplavskiy, S. V., Nesterov, A. Yu., Boyko, V. M. (2020). Razrabotka i primenenie lazernogo doplerovskogo anemometra s pryamym spektral'nym analizom dlya issledovaniya vysokoskorostnykh mnogofaznykh potokov. Teplofizika i aeromekhanika, 4, 583–591. Available at: https://www.sibran.ru/journals/issue.php?ID=180040&ARTICLE_ID=180048
  14. Arda, D. R., Mackley, M. R. (2005). The effect of die exit curvature, die surface roughness and a fluoropolymer additive on sharkskin extrusion instabilities in polyethylene processing. Journal of Non-Newtonian Fluid Mechanics, 126 (1), 47–61. doi: https://doi.org/10.1016/j.jnnfm.2004.12.005
  15. Clemeur, N., Rutgers, R. P. G., Debbaut, B. (2004). Numerical simulation of abrupt contraction flows using the Double Convected Pom–Pom model. Journal of Non-Newtonian Fluid Mechanics, 117 (2-3), 193–209. doi: https://doi.org/10.1016/j.jnnfm.2004.02.001
  16. Tachibana, M., Iemoto, Y. (1981). Steady Laminar Flow in the Inlet Region of Rectangular Ducts. Bulletin of JSME, 24 (193), 1151–1158. doi: https://doi.org/10.1299/jsme1958.24.1151
  17. Mazo, A. B. (2018). Vychislitel'naya gidrodinamika. Chast' 1. Matematicheskie modeli, setki i setochnye skhemy. Kazan': Kazanskiy universitet, 165. Available at: https://www.researchgate.net/publication/329702419_VYCISLITELNAA_GIDRODINAMIKA_Cast_1_Matematiceskie_modeli_setki_i_setocnye_shemy_Ucebnoe_posobie_Kazan-2018
  18. Kalinin, E. I., Mazo, A. B., Isaev, S. A. (2016). Composite mesh generator for CFD problems. IOP Conference Series: Materials Science and Engineering, 158, 012047. doi: https://doi.org/10.1088/1757-899x/158/1/012047
  19. Shlikhting, G. (1974). Teoriya pogranichnogo sloya. Moscow: Nauka, 742.
  20. Miller, E., Rothstein, J. P. (2004). Control of the sharkskin instability in the extrusion of polymer melts using induced temperature gradients. Rheologica Acta, 44 (2), 160–173. doi: https://doi.org/10.1007/s00397-004-0393-4
  21. Batra, R. L., K. Koshy, M. (1978). Effect of non-uniform inlet velocity profile in the entrance region of a Bingham plastic flow Between parallel plates. International Journal of Engineering Science, 16 (8), 579–589. doi: https://doi.org/10.1016/0020-7225(78)90022-8
  22. Tomita, Y. (1991). Velocity Profile in Viscoelastic Flow of a Tube. Journal of Chem. Enginering of Japan, 4, 115–118.
  23. Nosko, S. V. (2014). Research of hydrodynamic conditions of entrance in channels of process equipment. Eastern-European Journal of Enterprise Technologies, 3 (7 (69)), 49–54. doi: https://doi.org/10.15587/1729-4061.2014.24876
  24. Cherry, E. M., Padilla, A. M., Elkins, C. J., Eaton, J. K. (2010). Three-dimensional velocity measurements in annular diffuser segments including the effects of upstream strut wakes. International Journal of Heat and Fluid Flow, 31 (4), 569–575. doi: https://doi.org/10.1016/j.ijheatfluidflow.2010.02.029
Determining a flow structure in the region of local obstacles of different types taking into account the hydrodynamic conditions for entering the initial section

Downloads

Published

2023-04-30

How to Cite

Nosko, S., Kostiuk, D., Haletskyi, O., & Nochnichenko, I. (2023). Determining a flow structure in the region of local obstacles of different types taking into account the hydrodynamic conditions for entering the initial section. Eastern-European Journal of Enterprise Technologies, 2(7 (122), 24–32. https://doi.org/10.15587/1729-4061.2023.277342

Issue

Vol. 2 No. 7 (122) (2023): Applied mechanics

Section

Applied mechanics

License

Copyright (c) 2023 Serhii Nosko, Dmytro Kostiuk, Oleksandr Haletskyi, Ihor Nochnichenko

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.

A license agreement is a document in which the author warrants that he/she owns all copyright for the work (manuscript, article, etc.).
The authors, signing the License Agreement with TECHNOLOGY CENTER PC, have all rights to the further use of their work, provided that they link to our edition in which the work was published.
According to the terms of the License Agreement, the Publisher TECHNOLOGY CENTER PC does not take away your copyrights and receives permission from the authors to use and dissemination of the publication through the world's scientific resources (own electronic resources, scientometric databases, repositories, libraries, etc.).
In the absence of a signed License Agreement or in the absence of this agreement of identifiers allowing to identify the identity of the author, the editors have no right to work with the manuscript.
It is important to remember that there is another type of agreement between authors and publishers – when copyright is transferred from the authors to the publisher. In this case, the authors lose ownership of their work and may not use it in any way.