Development of a discreet-continuous mathematical model of a percussion device with parameters of influence on the characteristics of an impact pulse

Authors

DOI:

https://doi.org/10.15587/1729-4061.2023.290029

Keywords:

impact device, discrete-continuous model, co-impact force, boundary conditions, dissipative resistance

Abstract

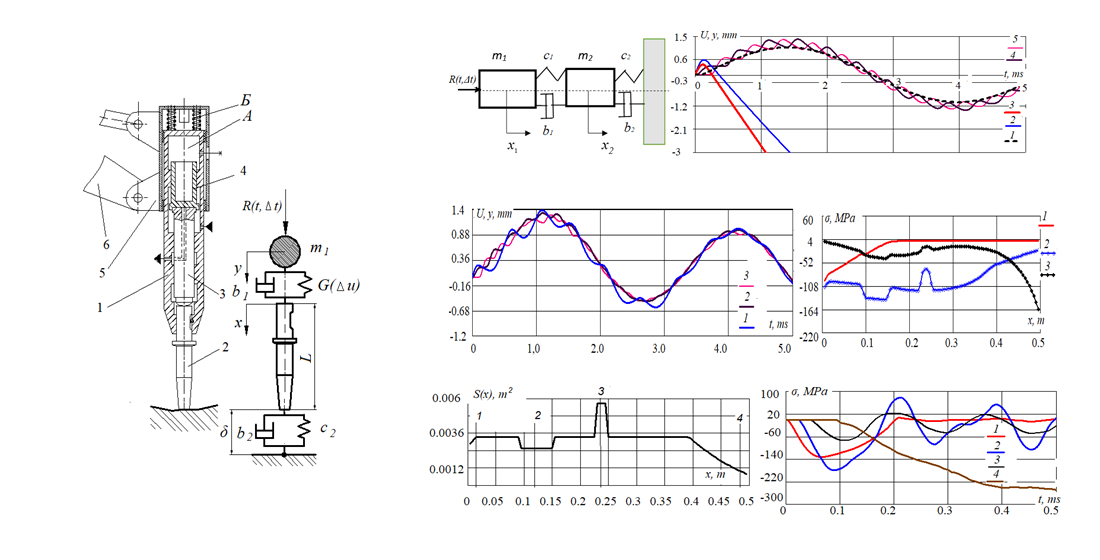
A study of a model of a discrete-continuous type of impactor in the energy transfer phase during the impact of a striker and a tool is presented. The device is used to destroy rocks, in construction equipment, and in the oil industry. In the mathematical model, the tool is represented by a rod with a variable profile, and the striker is a discrete element with a consolidated mass. The presence of rigid and dissipative connections models the impact interaction. The motion of the interacting elements of the impactor is described by a system of differential equations linked by boundary and initial conditions. The model allows determining the parameters of influence on the characteristic of the shock pulse at variable resistance of the working medium. The force of impact of a discrete element and the contact end of the rod is represented as a power law dependent on the difference in displacements of the contacting elements. The finite difference method is used to solve the initial boundary value problem. The parameters of the difference scheme were determined through modelling problems and were as follows: time step (1, ..., 5)·10-5 s; length step – (0.1...0.3) of the tool length, and for the mixed scheme – within 0.5...0.8. It was found that the time of striker-to-tool co-impact, depending on the stiffness coefficient, was 200...300 μs. With a load of up to 90 kN in the time range of 0...4 ms, the normal stresses in the tool sections at different times were 200...250 MPa. The combination of discrete and continuous elements simplifies the calculation scheme. It allows to determine the distribution of force characteristics in the cross-sections of the tool, the force and time of impact, and the influence of the working environment on these parameters. The developed model can be used to design impactors and optimize their parameters

Author Biographies

Viktor Slidenko, National Technical University of Ukraine “Igor Sikorsky Kyiv Polytechnic Institute”

Doctor of Technical Sciences, Associate Professor

Department of Automation of Electrical and Mechatronic Complexes

Oleksandr Slidenko, “Fenix-K” Limited Liability Company

PhD

Liubov Marchuk, National Technical University of Ukraine “Igor Sikorsky Kyiv Polytechnic Institute”

Postgraduate Student

Department of Automation of Electrical and Mechatronic Complexes

Viacheslav But, National Technical University of Ukraine “Igor Sikorsky Kyiv Polytechnic Institute”

Postgraduate Student

Department of Automation of Electrical and Mechatronic Complexes

References

  1. Xu, Q., Huang, Y. Y., Tian, X. Y. (2010). Present situation and development trends of hydraulic impactors research. Constraction Machinery and Equipment, 6, 47–62.
  2. Batako, A. D., Babitsky, V. I., Halliwell, N. A. (2004). Modelling of vibro-impact penetration of self-exciting percussive-rotary drill bit. Journal of Sound and Vibration, 271 (1-2), 209–225. doi: https://doi.org/10.1016/s0022-460x(03)00642-4
  3. Neyman, V., Neyman, L. (2017). Dynamical model the synchronous impact electromagnetic drive mechatronic modul. 12 International forum on strategic technology, 1, 188–193.
  4. Yu Neyman, V., Markov, A. V. (2018). Linear electromagnetic drive of impact machines with retaining striker. IOP Conference Series: Earth and Environmental Science, 194, 062023. doi: https://doi.org/10.1088/1755-1315/194/6/062023
  5. Yang, G., Fang, J. (2012). Structure Parameters Optimization Analysis of Hydraulic Hammer System. Modern Mechanical Engineering, 2 (4), 137–142. doi: https://doi.org/10.4236/mme.2012.24018
  6. Slidenko, V. M., Shevchuk, S. P., Zamaraieva, O. V., Listovshchyk, L. K. (2013). Adaptyvne funktsionuvannia impulsnykh vykonavchykh orhaniv hirnychykh mashyn. Kyiv: NTUU ”KPI”, 180.
  7. Zhukov, I. A., Molchanov, V. V. (2014). Rational Designing Two-Stage Anvil Block of Impact Mechanisms. Advanced Materials Research, 1040, 699–702. doi: https://doi.org/10.4028/www.scientific.net/amr.1040.699
  8. Zhukov, I. A., Dvornikov, L. T., Nikitenko, S. M. (2016). About creation of machines for rock destruction with formation of apertures of various cross-sections. IOP Conference Series: Materials Science and Engineering, 124, 012171. doi: https://doi.org/10.1088/1757-899x/124/1/012171
  9. Zhukov, I., Repin, A., Timofeev, E. (2018). Automated calculation and analysis of impacts generated in mining machine by anvil blocks of complex geometry. IOP Conference Series: Earth and Environmental Science, 134, 012071. doi: https://doi.org/10.1088/1755-1315/134/1/012071
  10. Slidenko, A. M., Slidenko, V. M., Valyukhov, S. G. (2021). Discrete-continuous three-element model of impact device. Journal of Physics: Conference Series, 2131 (3), 032091. doi: https://doi.org/10.1088/1742-6596/2131/3/032091
  11. Slidenko, A. M., Slidenko, V. M. (2019). Numerical research method of an impact device model. Journal of Physics: Conference Series, 1203, 012086. doi: https://doi.org/10.1088/1742-6596/1203/1/012086
  12. Vasylenko, M., Oleksiichuk, O. (2004). Teoriia kolyvan i stiikosti rukhu. Kyiv: Vyshcha shkola, 525.
  13. Samarskii, A. (2001). The Theory of Difference Schemes. Boca Raton: CRC Press, 786. doi: https://doi.org/10.1201/9780203908518
Development of a discreet-continuous mathematical model of a percussion device with parameters of influence on the characteristics of an impact pulse

Downloads

Published

2023-10-31

How to Cite

Slidenko, V., Slidenko, O., Marchuk, L., & But, V. (2023). Development of a discreet-continuous mathematical model of a percussion device with parameters of influence on the characteristics of an impact pulse. Eastern-European Journal of Enterprise Technologies, 5(7 (125), 70–79. https://doi.org/10.15587/1729-4061.2023.290029

Issue

Vol. 5 No. 7 (125) (2023): Applied mechanics

Section

Applied mechanics

License

Copyright (c) 2023 Viktor Slidenko, Oleksandr Slidenko, Liubov Marchuk, Viacheslav But

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.

A license agreement is a document in which the author warrants that he/she owns all copyright for the work (manuscript, article, etc.).
The authors, signing the License Agreement with TECHNOLOGY CENTER PC, have all rights to the further use of their work, provided that they link to our edition in which the work was published.
According to the terms of the License Agreement, the Publisher TECHNOLOGY CENTER PC does not take away your copyrights and receives permission from the authors to use and dissemination of the publication through the world's scientific resources (own electronic resources, scientometric databases, repositories, libraries, etc.).
In the absence of a signed License Agreement or in the absence of this agreement of identifiers allowing to identify the identity of the author, the editors have no right to work with the manuscript.
It is important to remember that there is another type of agreement between authors and publishers – when copyright is transferred from the authors to the publisher. In this case, the authors lose ownership of their work and may not use it in any way.