Determining the effect of a floating point on the Falcon digital signature algorithm security
DOI:
https://doi.org/10.15587/1729-4061.2024.295160Keywords:
quantum-resistant transformations, lattice-based cryptography, attack on implementation, NIST PQC, NTRUAbstract
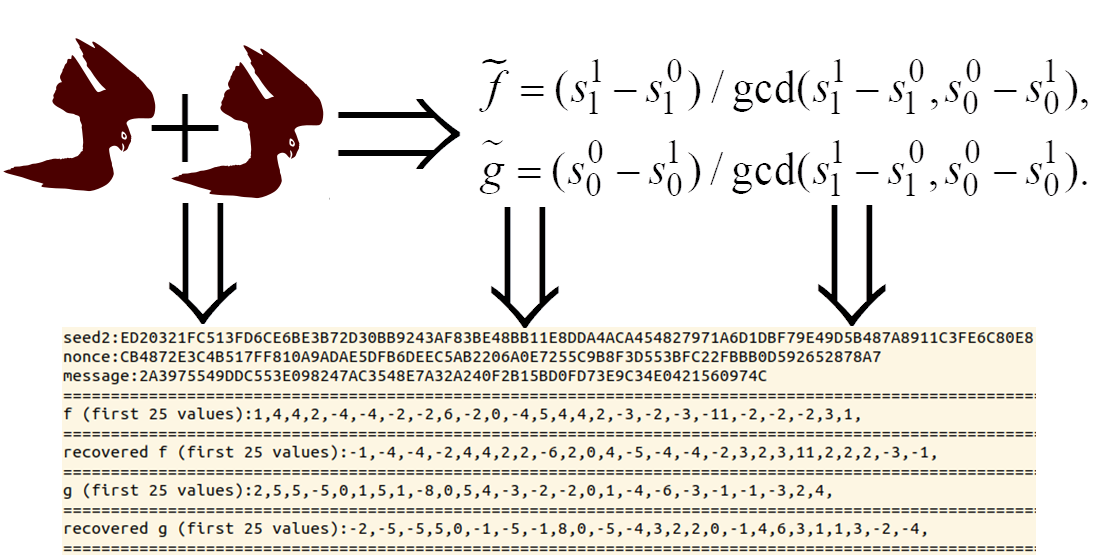
The object of research is digital signatures. The Falcon digital signature scheme is one of the finalists in the NIST post-quantum cryptography competition. Its distinctive feature is the use of floating-point arithmetic. However, floating-point arithmetic has so-called rounding noise, which accumulates during computations and in some cases may lead to significant changes in the processed values. The work considers the problem of using rounding noise to build attacks on implementation. The main result of the study is a novel attack on implementation, which enables the secret key recovery. This attack differs from existing attacks in using two separately secure implementations with different computation orders. As a result of the analysis, the conditions under which secret key recovery is possible were revealed. The attack requires 300,000 signatures and two implementations to recover key. The probability of successful attack ranges from 70 % to 76 %. This probability is explained by the structure of the Gaussian sampling algorithm used in the Falcon digital signature. At the same time, a necessary condition for conducting an attack is identical seed during signature generation. This condition makes the attack more theoretical than practical since the correct implementation of the Falcon makes probability of two identical seeds negligible. However, the possible usage of floating-point noise shows potential existence of additional attack vectors for the Falcon that should be covered in security models. The results could be used in the construction of digital signature security models and their implementation in existing information and communication systems
References
- Falcon: Fast-Fourier Lattice-based Compact Signatures over NTRU. Available at: https://falcon-sign.info/
- Post-Quantum Cryptography. NIST. Available at: https://csrc.nist.gov/projects/post-quantum-cryptography
- Tran, T., Liu, B. (1977). Accumulation of roundoff errors in floating point FFT. IEEE Transactions on Circuits and Systems, 24 (3), 132–143. https://doi.org/10.1109/tcs.1977.1084316
- Gentry, C., Peikert, C., Vaikuntanathan, V. (2008). How to Use a Short Basis:Trapdoors for hard lattices and new cryptographic constructions. Available at: https://eprint.iacr.org/2007/432.pdf
- Lyubashevsky, V., Prest, T. (2015). Quadratic Time, Linear Space Algorithms for Gram-Schmidt Orthogonalization and Gaussian Sampling in Structured Lattices. Lecture Notes in Computer Science, 789–815. https://doi.org/10.1007/978-3-662-46800-5_30
- Ducas, L., Nguyen, P. Q. (2012). Faster Gaussian Lattice Sampling Using Lazy Floating-Point Arithmetic. Lecture Notes in Computer Science, 415–432. https://doi.org/10.1007/978-3-642-34961-4_26
- Prest, T. (2015). Gaussian Sampling in Lattice-Based Cryptography. Paris: ENS PARIS. Available at: https://theses.hal.science/tel-01245066
- Prest, T. (2017). Sharper Bounds in Lattice-Based Cryptography Using the Rényi Divergence. Lecture Notes in Computer Science, 347–374. https://doi.org/10.1007/978-3-319-70694-8_13
- Ducas, L., Prest, T. (2016). Fast Fourier Orthogonalization. Proceedings of the ACM on International Symposium on Symbolic and Algebraic Computation. https://doi.org/10.1145/2930889.2930923
- Karabulut, E., Aysu, A. (2021). FALCON Down: Breaking FALCON Post-Quantum Signature Scheme through Side-Channel Attacks. 2021 58th ACM/IEEE Design Automation Conference (DAC). https://doi.org/10.1109/dac18074.2021.9586131
- Guerreau, M., Martinelli, A., Ricosset, T., Rossi, M. (2022). The Hidden Parallelepiped Is Back Again: Power Analysis Attacks on Falcon. IACR Transactions on Cryptographic Hardware and Embedded Systems, 2022 (3), 141–164. https://doi.org/10.46586/tches.v2022.i3.141-164
- Zhang, S., Lin, X., Yu, Y., Wang, W. (2023). Improved Power Analysis Attacks on Falcon. Lecture Notes in Computer Science, 565–595. https://doi.org/10.1007/978-3-031-30634-1_19
- Falcon source files (reference implementation). Available at: https://falcon-sign.info/impl/falcon.h.html
Downloads
Published
How to Cite
Issue
Section
License
Copyright (c) 2024 Oleksandr Potii, Olena Kachko, Serhii Kandii, Yevhenii Kaptol

This work is licensed under a Creative Commons Attribution 4.0 International License.
The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.
A license agreement is a document in which the author warrants that he/she owns all copyright for the work (manuscript, article, etc.).
The authors, signing the License Agreement with TECHNOLOGY CENTER PC, have all rights to the further use of their work, provided that they link to our edition in which the work was published.
According to the terms of the License Agreement, the Publisher TECHNOLOGY CENTER PC does not take away your copyrights and receives permission from the authors to use and dissemination of the publication through the world's scientific resources (own electronic resources, scientometric databases, repositories, libraries, etc.).
In the absence of a signed License Agreement or in the absence of this agreement of identifiers allowing to identify the identity of the author, the editors have no right to work with the manuscript.
It is important to remember that there is another type of agreement between authors and publishers – when copyright is transferred from the authors to the publisher. In this case, the authors lose ownership of their work and may not use it in any way.









