Identifying some regularities of the turbulent steady-state plane-parallel motion of incompressible fluid at the entrance length

Authors

DOI:

https://doi.org/10.15587/1729-4061.2024.302879

Keywords:

plane-parallel motion, hydrodynamic entrance region, turbulent motion, viscous fluid, velocity distribution

Abstract

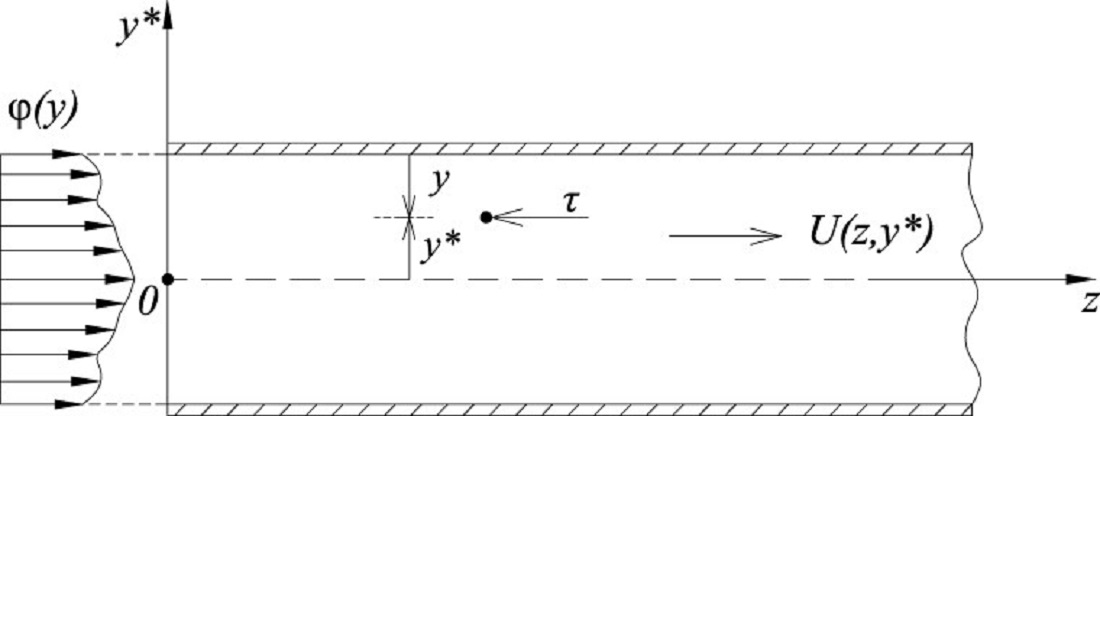
This paper investigates the structural changes in the turbulent motion of an incompressible fluid in the hydrodynamic entrance region of plane-parallel pressure motion. Movement in pressure hydromechanical systems usually occurs in a turbulent regime. Studying the patterns of changes in hydrodynamic parameters under conditions of stationary turbulent pressure motion in the inlet region is a very urgent task. The study was carried out on the basis of boundary layer equations. Taking into account the dependence of changes in the kinematic viscosity coefficient that occur between layers of fluid, a boundary value problem was formed. Analytical solutions have been obtained that make it possible to obtain patterns of changes in velocity and pressure in any effective flow section. Based on the general conclusions of the study, solutions were found for two cases:

  1. a) the velocity of the fluid entering the cylindrical pipe is constant;
  2. b) the velocity of the incoming fluid has a parabolic distribution.

For these cases, using computer analysis of the data obtained, general graphs of velocity changes were constructed in various sections along the hydrodynamic entrance region. These graphs, which display the change in velocity along the entire length of the inlet, make it possible to obtain the velocity of fluid movement at any point along the inlet length and estimate the length of the transition zone. The results obtained are among the least studied issues of classical fluid mechanics and are of important theoretical interest. The results obtained are applicable for the correct construction of the hydrodynamic entrance region of machinery. A calculation formula has been obtained to determine the length of the hydrodynamic inlet region

Author Biographies

Arestak Sarukhanyan, National University of Architecture and Construction of Armenia

Doctor of Technical Sciences, Professor, Head of Department

Department of Water Systems, Hydraulic Engineering and Hydropower

Garnik Vermishyan, National University of Architecture and Construction of Armenia

Candidate of Physics and Mathematics Sciences, Associate Professor

Department of Mathematics

Hovhannes Kelejyan, National University of Architecture and Construction of Armenia

Candidate of Technical Sciences, Associate Professor

Department Water Systems, Hydraulic Engineering and Hydropower

Armine Gevorgyan, National University of Architecture and Construction of Armenia

Candidate of Technical Sciences, Associate Professor

Department Water Systems, Hydraulic Engineering and Hydropower

References

  1. Targ, S. M. (1951). Fundamental Problems of Theory of Laminary Flows. Moscow: QITTL, 400.
  2. Sarukhanyan, A., Vardanyan, Y., Baljyan, P., Vermishyan, G. (2023). Pattern identification of the non-stationary laminar flow of a viscous fluid in the round pipe inlet section. Eastern-European Journal of Enterprise Technologies, 2 (7 (122)), 33–42. https://doi.org/10.15587/1729-4061.2023.278001
  3. Sarukhanyan, A., Vartanyan, A., Vermishyan, G., Tokmajyan, V. (2020). The Study of Hydrodynamic Processes Occurring on Transition of Sudden Expanding of Hydraulic Section of Plane – Parallel Full Pipe Flow. TEM Journal, 9 (4), 1494–1501. https://doi.org/10.18421/tem94-23
  4. Sarukhanyan, A., Vermishyan, G., Kelejyan, H. (2023). Plane-Parallel Laminar Flow of Viscous Fluid in the Transition Zone of the Inlet Section. Journal of Architectural and Engineering Research, 4, 75–85. https://doi.org/10.54338/27382656-2023.4-008
  5. Atabek, H. B., Chang, C. C. (1961). Oscillatory flow near the entry of a circular tube. Zeitschrift Für Angewandte Mathematik Und Physik ZAMP, 12 (3), 185–201. https://doi.org/10.1007/bf01592332
  6. Atabek, H. B., Chang, C. C., Fingerson, L. M. (1964). Measurement of Laminar Oscillatory Flow in the Inlet Length of a Circular Tube. Physics in Medicine and Biology, 9 (2), 219–227. https://doi.org/10.1088/0031-9155/9/2/309
  7. Avula, X. J. R. (1969). Analysis of suddenly started laminar flow in the entrance region of a circular tube. Applied Scientific Research, 21 (1), 248–259. https://doi.org/10.1007/bf00411611
  8. Crane, C. M. (1974). A new method for the numerical solution of time dependent viscous flow. Applied Scientific Research, 30 (1), 47–77. https://doi.org/10.1007/bf00385775
  9. Urbanowicz, K., Firkowski, M., Bergant, A. (2018). Comparing analytical solutions for unsteady laminar pipe flow. Conference: BHR Pressure Surges 2018. Available at: https://www.researchgate.net/publication/329759824_Comparing_analytical_solutions_for_unsteady_laminar_pipe_flow
  10. Vardy, A. E., Brown, J. M. B. (2010). Laminar pipe flow with time-dependent viscosity. Journal of Hydroinformatics, 13 (4), 729–740. https://doi.org/10.2166/hydro.2010.073
  11. Daprà, I., Scarpi, G. (2017). Unsteady Flow of Fluids With Arbitrarily Time-Dependent Rheological Behavior. Journal of Fluids Engineering, 139 (5). https://doi.org/10.1115/1.4035637
  12. Kannaiyan, A., Natarajan, S., Vinoth, B. R. (2022). Stability of a laminar pipe flow subjected to a step-like increase in the flow rate. Physics of Fluids, 34 (6). https://doi.org/10.1063/5.0090337
  13. Rocha, G. N., Poole, R. J., Oliveira, P. J. (2007). Bifurcation phenomena in viscoelastic flows through a symmetric 1:4 expansion. Journal of Non-Newtonian Fluid Mechanics, 141 (1), 1–17. https://doi.org/10.1016/j.jnnfm.2006.08.008
  14. Mullin, T., Seddon, J. R. T., Mantle, M. D., Sederman, A. J. (2009). Bifurcation phenomena in the flow through a sudden expansion in a circular pipe. Physics of Fluids, 21 (1). https://doi.org/10.1063/1.3065482
  15. Hawa, T., Rusak, Z. (2000). Viscous flow in a slightly asymmetric channel with a sudden expansion. Physics of Fluids, 12 (9), 2257–2267. https://doi.org/10.1063/1.1287610
  16. Fester, V., Mbiya, B., Slatter, P. (2008). Energy losses of non-Newtonian fluids in sudden pipe contractions. Chemical Engineering Journal, 145 (1), 57–63. https://doi.org/10.1016/j.cej.2008.03.003
  17. Chen, X., Hussain, F., She, Z.-S. (2018). Quantifying wall turbulence via a symmetry approach. Part 2. Reynolds stresses. Journal of Fluid Mechanics, 850, 401–438. https://doi.org/10.1017/jfm.2018.405
  18. Baidya, R., Philip, J., Hutchins, N., Monty, J. P., Marusic, I. (2017). Distance-from-the-wall scaling of turbulent motions in wall-bounded flows. Physics of Fluids, 29 (2). https://doi.org/10.1063/1.4974354
  19. Liu, L., Gadde, S. N., Stevens, R. J. A. M. (2021). Universal Wind Profile for Conventionally Neutral Atmospheric Boundary Layers. Physical Review Letters, 126 (10). https://doi.org/10.1103/physrevlett.126.104502
  20. Sun, B. (2019). Thirty years of turbulence study in China. Applied Mathematics and Mechanics, 40 (2), 193–214. https://doi.org/10.1007/s10483-019-2427-9
  21. Luchini, P. (2017). Universality of the Turbulent Velocity Profile. Physical Review Letters, 118 (22). https://doi.org/10.1103/physrevlett.118.224501
  22. Loicianski, L. G. (2003). Mechanics of Fluids and Gases. Moscow: Drofa, 840.
  23. Schlichting, H., Gersten, K. (2017). Boundary-Layer Theory. Springer Berlin Heidelberg. https://doi.org/10.1007/978-3-662-52919-5
  24. Tikhonov, A. N., Samarski, A. G. (1999). Equations of Mathematical Physics. Moscow: Nauka, 799.
Identifying some regularities of the turbulent steady-state plane-parallel motion of incompressible fluid at the entrance length

Downloads

Published

2024-04-30

How to Cite

Sarukhanyan, A., Vermishyan, G., Kelejyan, H., & Gevorgyan, A. (2024). Identifying some regularities of the turbulent steady-state plane-parallel motion of incompressible fluid at the entrance length. Eastern-European Journal of Enterprise Technologies, 2(7 (128), 47–55. https://doi.org/10.15587/1729-4061.2024.302879

Issue

Vol. 2 No. 7 (128) (2024): Applied mechanics

Section

Applied mechanics

License

Copyright (c) 2024 Arestak Sarukhanyan, Garnik Vermishyan, Hovhannes Kelejyan, Armine Gevorgyan

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.

A license agreement is a document in which the author warrants that he/she owns all copyright for the work (manuscript, article, etc.).
The authors, signing the License Agreement with TECHNOLOGY CENTER PC, have all rights to the further use of their work, provided that they link to our edition in which the work was published.
According to the terms of the License Agreement, the Publisher TECHNOLOGY CENTER PC does not take away your copyrights and receives permission from the authors to use and dissemination of the publication through the world's scientific resources (own electronic resources, scientometric databases, repositories, libraries, etc.).
In the absence of a signed License Agreement or in the absence of this agreement of identifiers allowing to identify the identity of the author, the editors have no right to work with the manuscript.
It is important to remember that there is another type of agreement between authors and publishers – when copyright is transferred from the authors to the publisher. In this case, the authors lose ownership of their work and may not use it in any way.