Development of a non-standard system for simplifying boolean functions

Authors

DOI:

https://doi.org/10.15587/1729-4061.2024.305826

Keywords:

simplification of Boolean functions, non-standard system, intervals of Boolean space, location of equivalent transformations

Abstract

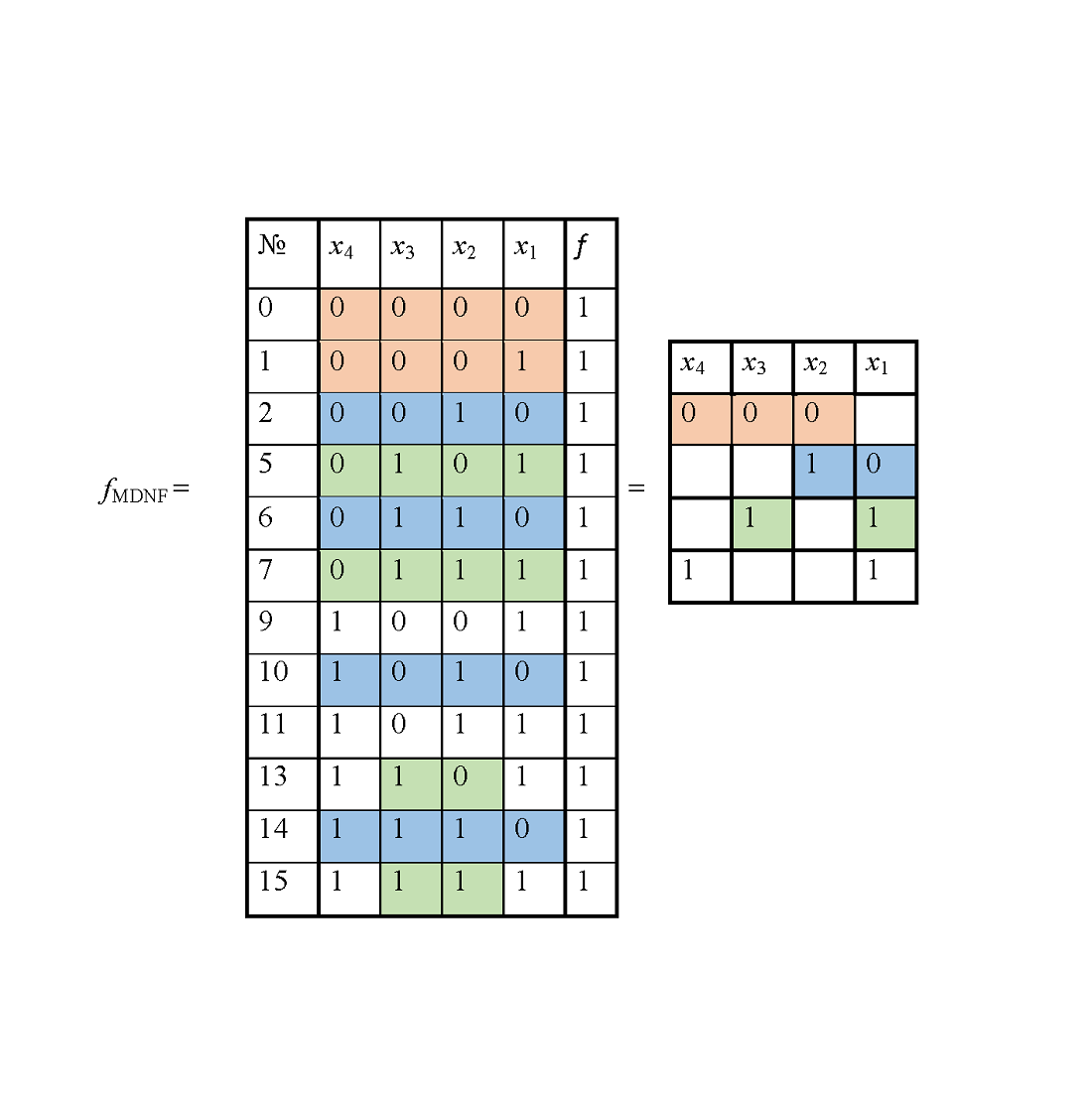
The object of this study is models of low-power digital logic circuits. The problem being solved is the effectiveness of the technique for simplifying Boolean functions to obtain optimal structures of logic circuits. A new theorem of a non-standard system of simplification of Boolean functions has been formulated, according to which in order to obtain a minimal function it will suffice to perform all non-redundant operations of simple and/or super-gluing of variables, which ultimately provides a minimal function in the main basis without using an implicant table. Thus, the problem of simplifying Boolean functions to the simplest normal equivalent is solved in one step. The interpretation of the result is that the properties of 2-(n, b)-design combinatorial systems make it possible to reproduce the definition of logical operations of super-gluing variables, to represent logical operations in a different way, and vice versa. This, in turn, ensures the establishment of the locations of equivalent transformations on the binary structure of the truth table and the implication of a systematic procedure for simplifying Boolean functions by an analytical method. Special feature of the results is that unambiguous identification of the locations of equivalent transformations is possible even when different intervals of the Boolean space containing the 2-(n, b)-design systems have common modules.

It has been experimentally confirmed that the non-standard system improves the efficiency of simplifying Boolean functions, including partially defined ones, by 200–300 % compared to analogs.

In terms of application, a non-standard system for simplifying Boolean functions will ensure the transfer of innovations to material production: from conducting fundamental research, expanding the capabilities of digital component design technology to organizing serial or mass production of novelties

Author Biography

Mykhailo Solomko, National University of Water and Environmental Engineering

PhD, Associate Professor

Department of Computer Engineering

References

  1. Riznyk, V., Solomko, M. (2018). Minimization of conjunctive normal forms of boolean functions by combinatorial method. Technology Audit and Production Reserves, 5 (2 (43)), 42–55. https://doi.org/10.15587/2312-8372.2018.146312
  2. Solomko, M., Batyshkina, I., Khomiuk, N., Ivashchuk, Y., Shevtsova, N. (2021). Developing the minimization of a polynomial normal form of boolean functions by the method of figurative transformations. Eastern-European Journal of Enterprise Technologies, 2 (4 (110)), 22–37. https://doi.org/10.15587/1729-4061.2021.229786
  3. Solomko, M., Khomiuk, N., Ivashchuk, Y., Nazaruk, V., Reinska, V., Zubyk, L., Popova, A. (2020). Implementation of the method of image transformations for minimizing the Sheffer functions. Eastern-European Journal of Enterprise Technologies, 5 (4 (107)), 19–34. https://doi.org/10.15587/1729-4061.2020.214899
  4. Solomko, M., Antoniuk, M., Voitovych, I., Ulianovska, Y., Pavlova, N., Biletskyi, V. (2023). Implementing the method of figurative transformations to minimize partially defined Boolean functions. Eastern-European Journal of Enterprise Technologies, 1 (4 (121)), 6–25. https://doi.org/10.15587/1729-4061.2023.273293
  5. Burmistrov, S. V., Khotunov, V. I., Zakharova, M. V., Mykhaylyuta, S. L., Liuta, M. V. (2023). Index method of minimization of Boolean functions. Bulletin of Cherkasy State Technological University, 2, 24–37. https://doi.org/10.24025/2306-4412.2.2023.273763
  6. Udovenko, A. (2023). DenseQMC: an efficient bit-slice implementation of the Quine-McCluskey algorithm. arXiv. https://doi.org/10.48550/arXiv.2302.10083
  7. Ignatiev, A., Previti, A., Marques-Silva, J. (2015). SAT-Based Formula Simplification. Theory and Applications of Satisfiability Testing -- SAT 2015, 287–298. https://doi.org/10.1007/978-3-319-24318-4_21
  8. Calò, E., Levy, J. (2023). General Boolean Formula Minimization with QBF Solvers. Artificial Intelligence Research and Development. https://doi.org/10.3233/faia230705
  9. Faroß, N., Schwarz, S. (2023). Gröbner Bases for Boolean Function Minimization. 8th International Workshop on Satisfiability Checking and Symbolic Computation. Available at: https://ceur-ws.org/Vol-3455/short4.pdf
  10. Le Charlier, B., Atindehou, M. M. (2016). A Method to Simplify Expressions: Intuition and Preliminary Experimental Results. EPiC Series in Computing. https://doi.org/10.29007/jv63
  11. Prasad, V. C. (2018). Novel method to simplify Boolean functions. Automatyka/Automatics, 22 (2), 29. https://doi.org/10.7494/automat.2018.22.2.29
  12. Siládi, V., Filo, T. (2013). Quine-Mccluskey algorithm on GPGPU. AWERProcedia Information Technology & Computer Science, 04, 814‒820. https://doi.org/10.13140/2.1.2113.1522
  13. Costamagna, A., De Micheli, G. (2023). Accuracy recovery: A decomposition procedure for the synthesis of partially-specified Boolean functions. Integration, 89, 248–260. https://doi.org/10.1016/j.vlsi.2022.12.008
  14. Boroumand, S., Bouganis, C.-S., Constantinides, G. A. (2021). Learning Boolean Circuits from Examples for Approximate Logic Synthesis. Proceedings of the 26th Asia and South Pacific Design Automation Conference. https://doi.org/10.1145/3394885.3431559
  15. Dimopoulos, A. C., Pavlatos, C., Papakonstantinou, G. (2022). Multi‐output, multi‐level, multi‐gate design using non‐linear programming. International Journal of Circuit Theory and Applications, 50 (8), 2960–2968. https://doi.org/10.1002/cta.3300
  16. Solomko, M. (2021). Developing an algorithm to minimize boolean functions for the visual-matrix form of the analytical method. Eastern-European Journal of Enterprise Technologies, 1 (4 (109)), 6–21. https://doi.org/10.15587/1729-4061.2021.225325
  17. Riznyk, V., Solomko, M. (2017). Application of super-sticking algebraic operation of variables for Boolean functions minimization by combinatorial method. Technology Audit and Production Reserves, 6 (2 (38)), 60–76. https://doi.org/10.15587/2312-8372.2017.118336
  18. McCluskey, E. J. (1956). Minimization of Boolean Functions. Bell System Technical Journal, 35 (6), 1417–1444. https://doi.org/10.1002/j.1538-7305.1956.tb03835.x
  19. Zakrevskiy, A. D. (1981). Logicheskiy sintez kaskadnyh shem. Moscow: Nauka, 416.
  20. Riznyk, V., Solomko, M., Tadeyev, P., Nazaruk, V., Zubyk, L., Voloshyn, V. (2020). The algorithm for minimizing Boolean functions using a method of the optimal combination of the sequence of figurative transformations. Eastern-European Journal of Enterprise Technologies, 3 (4 (105)), 43–60. https://doi.org/10.15587/1729-4061.2020.206308
  21. Rytsar, B. E. (1997). Metod minimizatsii bulevyh funktsiy. Problemy upravleniya i informatiki, 2, 100‒113.
  22. Rytsar, B. (1997). Minimization method of Boolean functions. SPIE Proceedings. https://doi.org/10.1117/12.284818
  23. Rytsar, B. Ye. (2005). Sposib pobudovy koniunktermovoho polia bulovoi funktsiyi. Visnyk Natsionalnoho universytetu "Lvivska politekhnika", 534, 21‒24. Available at: http://surl.li/siygp
  24. Minimizatsiya bulevyh funktsiy v klasse DNF. Available at: http://vuz.exponenta.ru/PDF/book/logic.pdf
  25. Kapuro, P. A. (2014). Tsifrovye funktsional'nye ustroystva v telekommunikatsiyah. Ch. 1: Bazovye tsifrovye funktsional'nye ustroystva. Minsk: BGUIR, 64. Available at: http://surl.li/siygv
  26. Rytsar, B. Ye. (2015). The Minimization Method of Boolean Functionns in Polynomial Set-theoretical Format. Conference: Proc. 24th Inter. Workshop, CS@P’2015. Vol. 2. Rzeszow, 130‒146. Available at: https://www.researchgate.net/publication/298158364_The_Minimization_Method_of_Boolean_Functionns_in_Polynomial_Set-theoretical_Format
  27. Solomko, M., Tadeyev, P., Zubyk, L., Babych, S., Mala, Y., Voitovych, O. (2021). Implementation of the method of figurative transformations to minimizing symmetric Boolean functions. Eastern-European Journal of Enterprise Technologies, 4 (4 (112)), 23–39. https://doi.org/10.15587/1729-4061.2021.239149
  28. Zakrevskiy, A. D., Pottosin, Yu. V., Cheremisinova, L. D. (2007). Logicheskie osnovy proektirovaniya diskretnyh ustroystv. Moscow: FIZMATLIT, 592.
  29. Rytsar, B. Ye., Belovolov, A. O. (2021). A New Method of the Logical Functions Minimization in the Polynomial Set-Theoretical Format. «Handshaking» Procedure. Control Systems and Computers, 1 (291), 03–14. https://doi.org/10.15407/csc.2021.01.003
  30. Rytsar, B. Ye. (2004). Teoretyko-mnozhynni optymizatsiyni metody lohikovoho syntezu kombinatsiynykh merezh. Lviv, 33. Available at: http://www.irbis-nbuv.gov.ua/publ/REF-0000263283
  31. Metod Kvayna ‒ Mak-Klaski nahozhdeniya sokrashchennoy DNF dvoichnoy funktsii. Available at: https://ematica.xyz/metodichki-i-knigi-po-matematike/kurs-lektcii-po-matematicheskoi-logike-i-teorii-algoritmov-aliev/6-1-metod-kvaina-mak-klaski-nakhozhdeniia-sokrashchennoi-dnf-dvoichnoi-funktcii
  32. Kupriyanova, D. V., Luk'yanova, I. V., Lutsik, Yu. A. (2021). Arifmeticheskie i logicheskie osnovy vychislitel'noy tehniki. Minsk: BGUIR, 72.
  33. Chong, K. H., Aris, I. B., Sinan, M. A., Hamiruce, B. M. (2007). Digital Circuit Structure Design via Evolutionary Algorithm Method. Journal of Applied Sciences, 7 (3), 380–385. https://doi.org/10.3923/jas.2007.380.385
  34. Coello Coello, C. A., Aguirre, A. H. (2002). Design of combinational logic circuits through an evolutionary multiobjective optimization approach. Artificial Intelligence for Engineering Design, Analysis and Manufacturing, 16 (1), 39–53. https://doi.org/10.1017/s0890060401020054
  35. Coello Coello, C. A., Hernandez Luna, E., Hernandez Aguirre, A. (2004). A comparative study of encodings to design combinational logic circuits using particle swarm optimization. Proceedings. 2004 NASA/DoD Conference on Evolvable Hardware, 2004. https://doi.org/10.1109/eh.2004.1310811
  36. Sysoienko, А. А., Sysoienko, S. V. (2023). Method for minimization of boolean functions with a large number of variables based on directed enumeration. Bulletin of Cherkasy State Technological University, 1, 42‒51. https://doi.org/10.24025/2306-4412.1.2023.274914
  37. Solomko, M., Batyshkina, I., Voitovych, I., Zubyk, L., Babych, S., Muzychuk, K. (2020). Devising a method of figurative transformations for minimizing boolean functions in the implicative basis. Eastern-European Journal of Enterprise Technologies, 6 (4 (108)), 32–47. https://doi.org/10.15587/1729-4061.2020.220094
  38. Riznyk, V. V., Solomko, M. T. (2017). Combinatorial method of minimizing boolean functions. Visnyk Natsionalnoho universytetu "Lvivska politekhnika". Serie: Kompiuterni systemy ta merezhi, 881, 135–151. https://doi.org/10.23939/csn2017.881.135
  39. Riznyk, V., Solomko, M. (2017). Minimization of Boolean functions by combinatorial method. Technology Audit and Production Reserves, 4 (2(36)), 49–64. https://doi.org/10.15587/2312-8372.2017.108532
  40. Riznyk, V., Solomko, M. (2018). Research of 5-bit boolean functions minimization protocols by combinatorial method. Technology Audit and Production Reserves, 4 (2 (42)), 41–52. https://doi.org/10.15587/2312-8372.2018.140351
  41. Markham Brown, F. (2010). McColl and Minimization. History and Philosophy of Logic, 31 (4), 337–348. https://doi.org/10.1080/01445340.2010.517387
  42. Quine, W. V. (1952). The Problem of Simplifying Truth Functions. The American Mathematical Monthly, 59 (8), 521–531. https://doi.org/10.1080/00029890.1952.11988183
Development of a non-standard system for simplifying boolean functions

Downloads

Published

2024-06-28

How to Cite

Solomko, M. (2024). Development of a non-standard system for simplifying boolean functions. Eastern-European Journal of Enterprise Technologies, 3(4 (129), 6–34. https://doi.org/10.15587/1729-4061.2024.305826

Issue

Vol. 3 No. 4 (129) (2024): Mathematics and Cybernetics - applied aspects

Section

Mathematics and Cybernetics - applied aspects

License

Copyright (c) 2024 Mykhailo Solomko

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.

A license agreement is a document in which the author warrants that he/she owns all copyright for the work (manuscript, article, etc.).
The authors, signing the License Agreement with TECHNOLOGY CENTER PC, have all rights to the further use of their work, provided that they link to our edition in which the work was published.
According to the terms of the License Agreement, the Publisher TECHNOLOGY CENTER PC does not take away your copyrights and receives permission from the authors to use and dissemination of the publication through the world's scientific resources (own electronic resources, scientometric databases, repositories, libraries, etc.).
In the absence of a signed License Agreement or in the absence of this agreement of identifiers allowing to identify the identity of the author, the editors have no right to work with the manuscript.
It is important to remember that there is another type of agreement between authors and publishers – when copyright is transferred from the authors to the publisher. In this case, the authors lose ownership of their work and may not use it in any way.