Mathematical and computer identification of the characteristics of oscillation frequency and deformations of the equipment element in the flush purification unit
DOI:
https://doi.org/10.15587/1729-4061.2024.308937Keywords:
computer simulation, mathematical examination, purification unit, graphical images, vibrating screen, frequencyAbstract
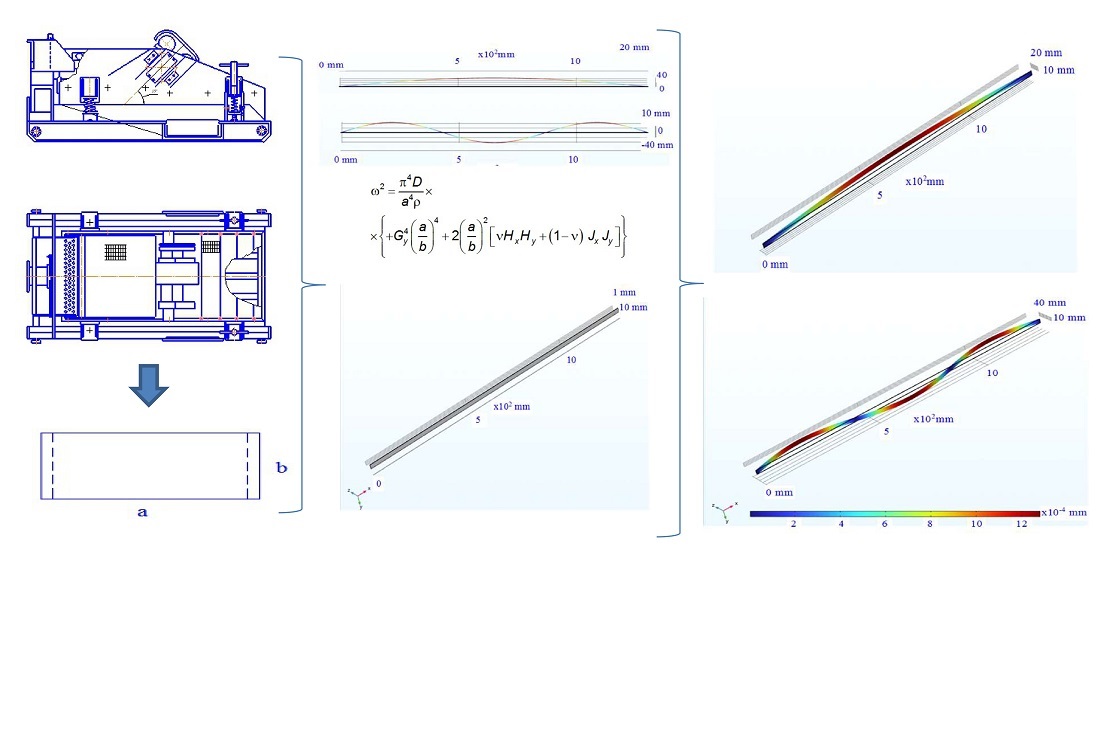
The object of research is an element of equipment in a vibrating screen, which is an active working body in the form of a plate.
The key element in the system of the flush purification unit is the vibrating screen. The basic design of the sieve does not allow the flush solution to be distributed evenly over the entire working surface. The concentration of drilling fluid in the central part of the equipment leads to premature abrasive wear and failure of the working element. Therefore, the structure of the vibrating screen needs to be improved in order to extend its service life. This task has been solved through the introduction of an active element to the structure for the redistribution of the solution through additional transverse vibrations.
The use of such an active element is an important step for improving the quality and efficiency of the purification system, which could optimize production processes and reduce costs in industry.
Taking into account transverse vibrations and calculating frequency parameters could help improve the design and use the vibrating screen more productively.
An analysis of the frequencies of oscillations of the active element-plate for cleaning the flush liquid with a vibrating screen was performed and a comparison of the analytically obtained results with the simulation data using the finite element method in the COMSOL Multiphysics software was carried out. The results are the basis for designing vibrating screens, conducting experimental and industrial research, and testing the screens. Computer studies have confirmed the possibility of using the improved design of the vibrating screen. By comparing the results of the calculation and computer simulation, the error was determined to be within 5 %.
The identified patterns could make it possible to select the plate oscillation frequencies depending on the known initial parameters, which would be useful for solving similar tasks.
References
- Surzhko, N. O., Savyk, V. M., Molchanov, P. O., Kaliuzhnyi, A. P. (2020). The efficiency increase of equipment work for the cleaning block of washing fluid. Zbirnyk naukovykh prats. Haluzeve mashynobuduvannia, budivnytstvo, 2 (55), 121–127. Available at: https://reposit.nupp.edu.ua/handle/PoltNTU/10187
- Surzhko, T., Knysh, M., Kuzub, Y., Kruchkov, O., Rubel, V. (2023). Study of the operating parameters of vibrations of a vibrosieve of the washing liquid purification unit. Technology Audit and Production Reserves, 4 (1 (72)), 34–39. https://doi.org/10.15587/2706-5448.2023.286362
- Kim, K., Kim, K., Han, C., Jang, Y., Han, P. (2020). A method for natural frequency calculation of the functionally graded rectangular plate with general elastic restraints. AIP Advances, 10 (8). https://doi.org/10.1063/5.0013625
- Kashmira Ajay Puranik, Surbhi R Tharewal, Monica S Mhetre. (2017). Eigen Frequency Vibration Analysis for Thin Plate. International Journal of Engineering Research And, 6 (03). https://doi.org/10.17577/ijertv6is030291
- Nesterenko, M. P., Molchanov, P. O. (2014). Rol vibrosyt v yakosti ochystky burovoho rozchynu. Zbirnyk naukovykh prats. Seriya: Haluzeve mashynobuduvannia, budivnytstvo, 1 (40), 82–90.
- Rubel, V., Rubel, V., Surzhko, T., Goshovskyi, S. (2024). Determining the effect of vibrating wave swabbing on the functional processes in carbonate low-permeability reservoirs. Engineering Technological Systems, 2 (1 (128)), 14–20. https://doi.org/10.15587/1729-4061.2024.299970
- Liakh, M. M., Fedoliak, N. V. (2016). Doslidzhennia vplyvu zminnykh parametriv na traiektoriyu rukhu vibroramy burovoho vibrosyta. Rozvidka ta rozrobka naftovykh i hazovykh rodovyshch, 3, 71–78. Available at: http://nbuv.gov.ua/UJRN/rrngr_2016_3_10
- Liakh, M. M., Fedoliak, N. V., Vakaliuk, V. M. (2015). Doslidzhennia vplyvu kolyvalnykh rukhiv sitky na efektyvnist roboty vibrosyta. Rozvidka ta rozrobka naftovykh i hazovykh rodovyshch, 4, 36–42. Available at: http://nbuv.gov.ua/UJRN/rrngr_2015_4_6
- Berezhnytskyi, B. S. (2016). Doslidzhennia kinematychnykh i dynamichnykh parametriv vibrosyt. Prykarpatskyi visnyk NTSh «Chyslo», 1, 328–336.
- Haţiegan, L. (Barboni), Haţiegan, C., Gillich, G. R., Hamat, C. O., Vasile, O., Stroia, M. D. (2018). Natural frequencies of thin rectangular plates clamped on contour using the Finite Element Method. IOP Conference Series: Materials Science and Engineering, 294, 012033. https://doi.org/10.1088/1757-899x/294/1/012033
- Alanbay, B., Kapania, R. K., Batra, R. C. (2020). Up to lowest 100 frequencies of rectangular plates using Jacobi polynomials and TSNDT. Journal of Sound and Vibration, 480, 115352. https://doi.org/10.1016/j.jsv.2020.115352
- Ilanko, S., Monterrubio, L. E., Mochida, Y. (2014). Natural Frequencies and Modes of Plates of Rectangular Planform. The Rayleigh–Ritz Method for Structural Analysis, 113–131. https://doi.org/10.1002/9781118984444.ch10
- Leissa, A. W. (1973). The free vibration of rectangular plates. Journal of Sound and Vibration, 31 (3), 257–293. https://doi.org/10.1016/s0022-460x(73)80371-2
- Timoshenko, S., Woinowsky-Krieger, S. (1959). Theory of plates and shells. New York: McGraw-Hill, 580. Available at: https://www.cap-recifal.com/ccs_files/articles/cuveaqua1_denisio/Timoshenko_-_Theory_of_plates_and_shells.pdf
Downloads
Published
How to Cite
Issue
Section
License
Copyright (c) 2024 Tetiana Surzhko, Petro Molchanov, Serhii Hudz, Maksym Knysh, Yuliya Sribna, Larysa Hrytsenko, Valerii Tytarenko, Vasyl Savyk, Victoriia Rubel

This work is licensed under a Creative Commons Attribution 4.0 International License.
The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.
A license agreement is a document in which the author warrants that he/she owns all copyright for the work (manuscript, article, etc.).
The authors, signing the License Agreement with TECHNOLOGY CENTER PC, have all rights to the further use of their work, provided that they link to our edition in which the work was published.
According to the terms of the License Agreement, the Publisher TECHNOLOGY CENTER PC does not take away your copyrights and receives permission from the authors to use and dissemination of the publication through the world's scientific resources (own electronic resources, scientometric databases, repositories, libraries, etc.).
In the absence of a signed License Agreement or in the absence of this agreement of identifiers allowing to identify the identity of the author, the editors have no right to work with the manuscript.
It is important to remember that there is another type of agreement between authors and publishers – when copyright is transferred from the authors to the publisher. In this case, the authors lose ownership of their work and may not use it in any way.









