Synthesis of expert matrices in inductive system-analytical research based on fuzzy logic algorithm

Authors

DOI:

https://doi.org/10.15587/1729-4061.2024.310326

Keywords:

inductive approach, fuzzy logic, criterion of relevance, criterion of corelevance, expert evaluations

Abstract

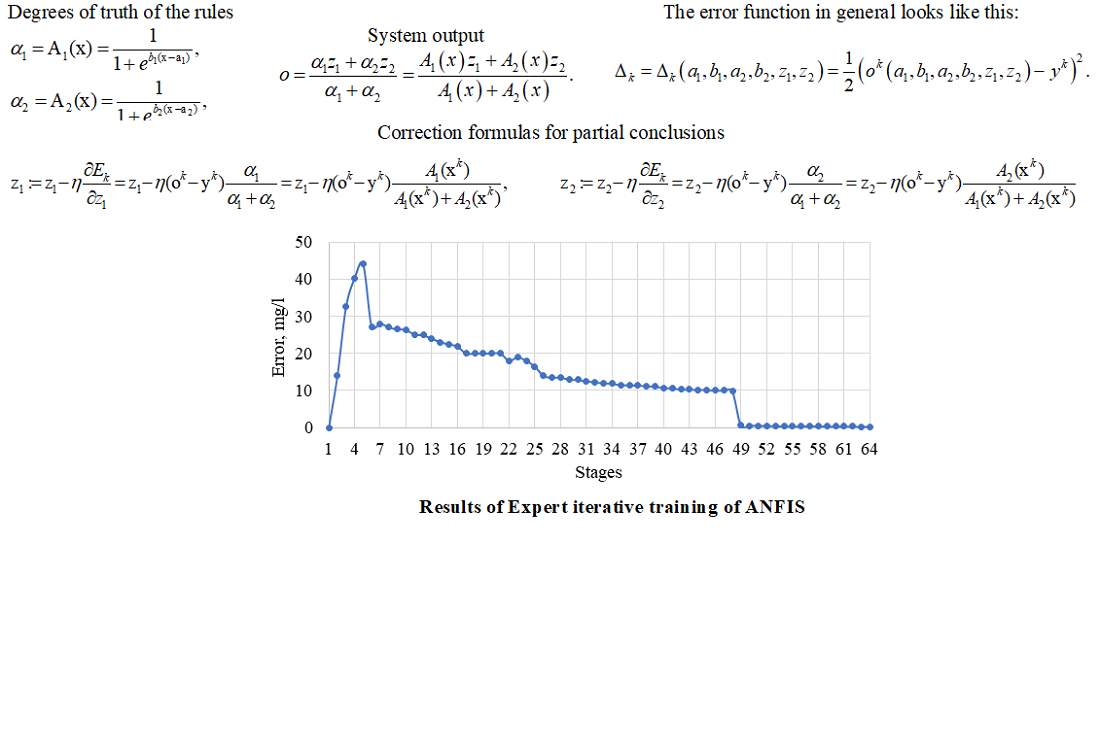
The object of research is the process of inductive modeling of complex systems. The studies that were conducted related to the application of algorithms of the fuzzy logic theory were to coordinate the conclusions of top-level experts in system information-analytical research (SIAR) in the tasks of innovative design. The possibilities of constructing elements of expert matrices of results, as well as evaluating the effectiveness of such applications, are defined. Thanks to this, obtaining formal expert evaluations in numerical form became possible. Experimental studies have confirmed that the proposed approach to the application of fuzzy logic algorithms to the construction of matrices of expert evaluations of SIAR results is quite effective and simple to implement. In addition, this approach fits well into the general paradigm of the Group Method of Data Handling (GMDH). In particular, it was established that the possibility of «retraining» such a block without significant efforts of professional experts can have a positive result, as well as have a good effect on the economic and time parameters of the research project. The main calculation formulas for the algorithm for building a fuzzy system using a neural network in a system with two rules are given. The construction of a fuzzy information output system trained on expert evaluations in the Matlab system is shown. As a result, a technologically acceptable standard deviation of 0.28268 mg/l was obtained. It has been established that by accumulating a database (knowledge) and/or using an information monitoring system, it is possible to «additionally train» a fuzzy system periodically or according to the established quality criterion in the program mode, without involving experts in this process. Thus, there are reasons to assert the importance of using a fuzzy system as one of the tools in inductive SIAR procedures

Author Biographies

Volodymyr Osypenko, Kyiv National University of Technologies and Design

Doctor of Technical Sciences, Professor

Department of Computer Science

Hanna Korohod, Kyiv National University of Technologies and Design

PhD, Associate Professor

Department of Computer Science

Borys Zlotenko, Kyiv National University of Technologies and Design

Doctor of Technical Sciences, Professor

Dean of Faculty of Mechatronics and Computer Technologies

Department of Computer Engineering and Electromechanics

Nataliia Chuprynka, Kyiv National University of Technologies and Design

PhD, Associate Professor, Head of Department

Department of Computer Science

Volodymyr Yakhno, Kyiv National University of Technologies and Design

PhD, Senior Lecturer

Department of Computer Science

References

  1. Ivakhnenko, A. G. (1970). Heuristic self-organization in problems of engineering cybernetics. Automatica, 6 (2), 207–219. https://doi.org/10.1016/0005-1098(70)90092-0
  2. Madala, H. R., Ivakhnenko, A. G. (2019). Inductive Learning Algorithms for Complex Systems Modeling. CRC Press. https://doi.org/10.1201/9781351073493
  3. Osypenko, V. (2013). Info-logical structure of inductive technologies of the searching system-information-analytical researches. Visnyk Natsionalnoho universytetu «Lvivska politekhnika». Ser. "Komp. nauky ta informatsiyni tekhnolohiyi", 751, 315–319.
  4. Osypenko, V. (2012). The Results Estimation in the Integrated System-Analytical Investigations Technologies. Control systems and computers, 1, 26–31. Available at: http://usim.org.ua/arch/2012/1/6.pdf
  5. Seno, P. S. (2007). Teoriya ymovirnostei ta matematychna statystyka. Kyiv: Znannia, 556.
  6. Wackerly, D., Mendenhall, W., Scheaffer, R. (2007). Mathematical Statistics with Applications. Brooks/Cole.
  7. Dalkey, N., Helmer, O. (1963). An Experimental Application of the DELPHI Method to the Use of Experts. Management Science, 9 (3), 458–467. https://doi.org/10.1287/mnsc.9.3.458
  8. Saaty, T. L. (2008). Relative measurement and its generalization in decision making why pairwise comparisons are central in mathematics for the measurement of intangible factors the analytic hierarchy/network process. Revista de La Real Academia de Ciencias Exactas, Fisicas y Naturales. Serie A. Matematicas, 102 (2), 251–318. https://doi.org/10.1007/bf03191825
  9. Andrieu, P., Cohen-Boulakia, S., Couceiro, M., Denise, A., Pierrot, A. (2023). A unifying rank aggregation framework to suitably and efficiently aggregate any kind of rankings. International Journal of Approximate Reasoning, 162, 109035. https://doi.org/10.1016/j.ijar.2023.109035
  10. Osypenko, V. (2011). Syntez ekspertnoi matrytsi za metrykoiu Kemeni v induktyvnykh tekhnolohiyakh informatsiyno-analitychnykh doslidzhen. Naukovyi visnyk NUBiP Ukrainy: Seriya «Enerhetyka i avtomatyzatsiya v APK», 166 (3), 119–127.
  11. Bury, H., Wagner, D. (2003). Application of Kemeny’s Median for Group Decision Support. Applied Decision Support with Soft Computing, 235–262. https://doi.org/10.1007/978-3-540-37008-6_10
  12. Davenport, A., Kalagnanam, J. (2004). A Computational Study of the Kemeny Rule for Preference Aggregation. AAAI’04, 697–702. Available at: https://cdn.aaai.org/AAAI/2004/AAAI04-110.pdf
  13. Zadeh, L. A. (1965). Fuzzy sets. Information and Control, 8 (3), 338–353. https://doi.org/10.1016/s0019-9958(65)90241-x
  14. Zadeh, L. A. (1994). Fuzzy logic, neural networks, and soft computing. Communications of the ACM, 37 (3), 77–84. https://doi.org/10.1145/175247.175255
  15. Bede, B. (2013). Mathematics of Fuzzy Sets and Fuzzy Logic. In Studies in Fuzziness and Soft Computing. Springer Berlin Heidelberg. https://doi.org/10.1007/978-3-642-35221-8
  16. Pal, N. R., Saha, S. (2008). Simultaneous Structure Identification and Fuzzy Rule Generation for Takagi–Sugeno Models. IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics), 38 (6), 1626–1638. https://doi.org/10.1109/tsmcb.2008.2006367
  17. Yadav, O. P., Singh, N., Chinnam, R. B., Goel, P. S. (2003). A fuzzy logic based approach to reliability improvement estimation during product development. Reliability Engineering & System Safety, 80 (1), 63–74. https://doi.org/10.1016/s0951-8320(02)00268-5
  18. Mehmanpazir, F., Asadi, S. (2016). Development of an evolutionary fuzzy expert system for estimating future behavior of stock price. Journal of Industrial Engineering International, 13 (1), 29–46. https://doi.org/10.1007/s40092-016-0165-7
  19. Sonbol, A. H., Fadali, M. S., Jafarzadeh, S. (2012). TSK Fuzzy Function Approximators: Design and Accuracy Analysis. IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics), 42 (3), 702–712. https://doi.org/10.1109/tsmcb.2011.2174151
  20. Alcala-Fdez, J., Alcala, R., Herrera, F. (2011). A Fuzzy Association Rule-Based Classification Model for High-Dimensional Problems With Genetic Rule Selection and Lateral Tuning. IEEE Transactions on Fuzzy Systems, 19 (5), 857–872. https://doi.org/10.1109/tfuzz.2011.2147794
  21. Adriaenssens, V., Baets, B. D., Goethals, P. L. M., Pauw, N. D. (2004). Fuzzy rule-based models for decision support in ecosystem management. Science of The Total Environment, 319 (1-3), 1–12. https://doi.org/10.1016/s0048-9697(03)00433-9
  22. Osypenko, V. V. (2014). Dva pidkhody do rozviazannia zadachi klasteryzatsiyi u shyrokomu sensi z pozytsiy induktyvnoho modeliuvannia. Energy and Automation, 1, 83–97. Available at: https://journals.nubip.edu.ua/index.php/Energiya/article/view/3433
  23. Ross, T. J. (2010). Fuzzy Logic with Engineering Applications. Wiley. https://doi.org/10.1002/9781119994374
  24. Passino, K. M., Yurkovich, S. (1997). Fuzzy Control. Addison-Wesley.
  25. Shi, Y., Mizumoto, M. (2000). A new approach of neuro-fuzzy learning algorithm for tuning fuzzy rules. Fuzzy Sets and Systems, 112 (1), 99–116. https://doi.org/10.1016/s0165-0114(98)00238-3
  26. Osypenko, V. V., Shtepa, V. N. (2010). Alhorytmy syntezu ekspertnoi matrytsi informatsiyno-analitychnykh doslidzhen na osnovi fazilohiky. Systemni tekhnolohiyi, 6 (71), 154–165. Available at: https://journals.nmetau.edu.ua/index.php/st/issue/view/76/51
  27. Shtepa, V. N., Donchenko, M. I., Sribnaya, O. G. (2007). Ochistka rastvorov ot dispersnyh primesey metodom elektrokoagulyatsii. 1. Elektrohimicheskoe poluchenie koagulyanta. Vistnyk NTU «KhPI». Khimiya, khimichna tekhnolohiya ta ekolohiya, 9, 86–94.
Synthesis of expert matrices in inductive system-analytical research based on fuzzy logic algorithm

Downloads

Published

2024-08-30

How to Cite

Osypenko, V., Korohod, H., Zlotenko, B., Chuprynka, N., & Yakhno, V. (2024). Synthesis of expert matrices in inductive system-analytical research based on fuzzy logic algorithm. Eastern-European Journal of Enterprise Technologies, 4(4 (130), 54–62. https://doi.org/10.15587/1729-4061.2024.310326

Issue

Vol. 4 No. 4 (130) (2024): Mathematics and Cybernetics - applied aspects

Section

Mathematics and Cybernetics - applied aspects

License

Copyright (c) 2024 Volodymyr Osypenko, Hanna Korohod, Borys Zlotenko, Nataliia Chuprynka, Volodymyr Yakhno

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.

A license agreement is a document in which the author warrants that he/she owns all copyright for the work (manuscript, article, etc.).
The authors, signing the License Agreement with TECHNOLOGY CENTER PC, have all rights to the further use of their work, provided that they link to our edition in which the work was published.
According to the terms of the License Agreement, the Publisher TECHNOLOGY CENTER PC does not take away your copyrights and receives permission from the authors to use and dissemination of the publication through the world's scientific resources (own electronic resources, scientometric databases, repositories, libraries, etc.).
In the absence of a signed License Agreement or in the absence of this agreement of identifiers allowing to identify the identity of the author, the editors have no right to work with the manuscript.
It is important to remember that there is another type of agreement between authors and publishers – when copyright is transferred from the authors to the publisher. In this case, the authors lose ownership of their work and may not use it in any way.