Implementation of a non-standard system for simplifying Peirce-Webb functions

Authors

DOI:

https://doi.org/10.15587/1729-4061.2024.312968

Keywords:

DNF simplification, Peirce-Webb function, Peirce-Webb basis, non-standard system, logical circuit, AND-NOT, OR-NOT gates

Abstract

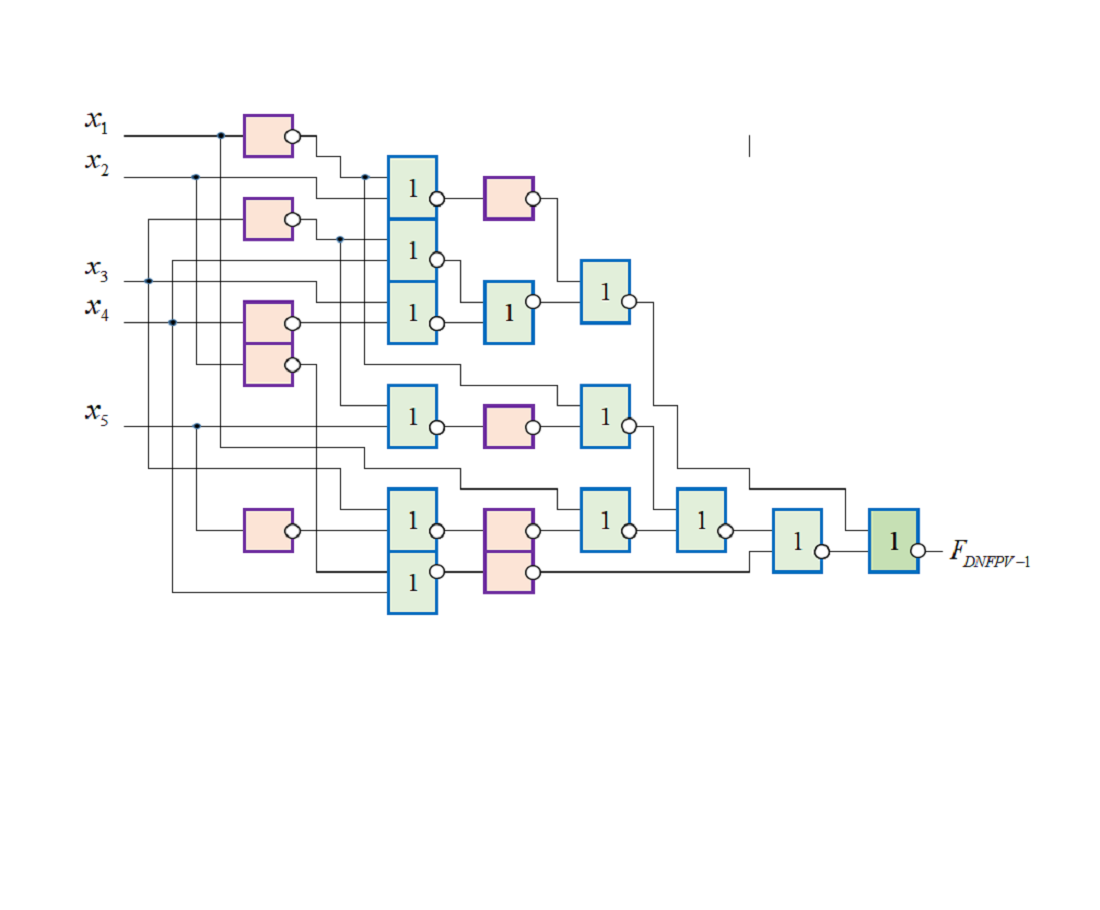
The object of research are models of optimal logic circuits based on universal Peirce-Webb functions. The problem solved is the efficiency of the technique for simplifying the Peirce-Webb functions. The extension of the non-standard system to the simplification of Peirce-Webb functions makes it possible to discover new rules of equivalent transformations of Boolean functions, and to complete the simplification procedure in one step. A feature of the simplification of functions in the Peirce-Webb basis by a non-standard system is fixing the digital project at the level of abstraction, followed by the application of the mechanism of logical synthesis to generate the corresponding equivalent at the level of gates of the logic circuit. The result of the transformation of the terms of the binary matrix in the end is some combinatorial system, metadata that can explain other data, for example, determine the minimum function for another logical basis.

The interpretation of the result consists in the use of combinatorial properties of binary structures of functions in the Peirce-Webb basis and binary structures of functions in the basic basis. These properties do not depend on the selected logical basis, which makes it possible to carry out equivalent transformations on binary matrices of Peirce-Webb functions according to the rules of the algebra of the main basis.

It has been experimentally confirmed that a non-standard system enables:

– to reduce the algorithmic complexity of simplifying the Peirce-Webb functions;

– to increase the performance of the simplification of Peirce-Webb functions by 200–300 %;

– to demonstrate the visibility of the process of simplifying functions.

In terms of application, the non-standard system of simplifying the Peirce-Webb functions could ensure the transfer of innovations to material production: from conducting fundamental research, expanding the capabilities of digital component design technology to organizing serial or mass production of novelties.

Author Biographies

Mykhailo Solomko, National University of Water and Environmental Engineering

PhD, Associate Professor

Department of Computer Engineering

Petro Tadeyev, National University of Water and Environmental Engineering

PhD, Doctor of Pedagogical Sciences, Professor

Department of Higher Mathematics

Mykola Antoniuk, Rivne State University of Humanities

PhD, Associate Professor

Department of Information and Communication Technologies and Methods of Teaching Informatics

Yuliia Mala, University of Customs and Finance

PhD

Department of Computer Science and Software Engineering

Stepaniia Babych, Rivne State University of Humanities

PhD, Associate Professor

Department of Information Technologies and Modeling

Yakiv Ivashchuk, National University of Water and Environmental Engineering

PhD

Department of Higher Mathematics

References

  1. Pucknell, D. A. (1990). Fundamentals of Digital Logic Design, With VLSI Circuit applications. Prentice Hall, 472.
  2. Mano, M., Kime, C. (2004). Logic and Computer Design Fundamentals. Prentice Hall.
  3. Baranov, S. (2008). Logic and System Design of Digital Systems. Tallinn: TUT Press.
  4. Micheli, G. (1994). Synthesis and Optimization of Digital Circuits. McGraw-Hill.
  5. Zakrevskij, A., Pottosin Yu., Cheremisinova, L. (2009). Optimization in Boolean Space. Tallinn: TUT Press.
  6. Baranov, S., Karatkevich, A. (2018). On Transformation of a Logical Circuit to a Circuit with NAND and NOR Gates Only. INTL JOURNAL OF ELECTRONICS AND TELECOMMUNICATIONS, 64 (3), 373–378. Available at: https://journals.pan.pl/dlibra/publication/123535/edition/107750/content
  7. Maxfield, M. (2018). Implementing and Converting Logic Circuits Using Only NAND or NOR Gates. Available at: https://www.eeweb.com/implementing-logic-functions-using-only-nand-or-nor-gates/
  8. Poomiga, M., Ananthi, M., Sinega, M., Aashika, S M., Nambi Rajan, M. (2021). Optimization of simple combinational universal logic gates. International Research Journal of Modernization in Engineering Technology and Science, 03 (08), 1000‒1006. Available at: https://www.irjmets.com/uploadedfiles/paper/volume_3/issue_8_august_2021/15911/final/fin_irjmets1630308031.pdf
  9. Olenev, A., Potekhina, E., Khabarov, A., Zvereva, L. (2024). Information and logical transformations in Schaeffer and Pierce Bases in Maple. ITM Web of Conferences, 59, 02006. https://doi.org/10.1051/itmconf/20245902006
  10. Menshikh, V. V., Nikitenko, V. A. (2022). Minimization of representations of the logical function in schaeffer and pierce bases. Bulletin of the South Ural State University Series “Mathematics. Mechanics. Physics,” 14 (4), 20–27. https://doi.org/10.14529/mmph220403
  11. Barland, I. (2012). An algorithm to implement a boolean function using only NAND's or only NOR's. Rice University. Available at: https://archive.org/details/cnx-org-col10347/page/n1/mode/2up
  12. Rajaei, A., Houshmand, M., Rouhani, M. (2011). Optimization of Combinational Logic Circuits Using NAND Gates and Genetic Programming. Soft Computing in Industrial Applications, 405–414. https://doi.org/10.1007/978-3-642-20505-7_36
  13. Dychka, I. A., Tarasenko, V. P., Onai, M. V. (2019). Osnovy prykladnoi teorii tsyfrovykh avtomativ. Kyiv, 505.
  14. Kalyadin, N. I. (2006). Praktikum po diskretnoy matematike (Chast' IV. Minimizatsiya FAL). Izhevsk: Izd-vo IzhGTU, 48.
  15. Riznyk, V., Solomko, M. (2017). Application of super-sticking algebraic operation of variables for Boolean functions minimization by combinatorial method. Technology Audit and Production Reserves, 6 (2 (38)), 60–76. https://doi.org/10.15587/2312-8372.2017.118336
  16. Solomko, M., Antoniuk, M., Voitovych, I., Ulianovska, Y., Pavlova, N., Biletskyi, V. (2023). Implementing the method of figurative transformations to minimize partially defined Boolean functions. Eastern-European Journal of Enterprise Technologies, 1 (4 (121)), 6–25. https://doi.org/10.15587/1729-4061.2023.273293
  17. Solomko, M. (2024). Development of a non-standard system for simplifying boolean functions. Eastern-European Journal of Enterprise Technologies, 3 (4 (129)), 6–34. https://doi.org/10.15587/1729-4061.2024.305826
  18. Kondratenko, N. R. (2010). Kompiuternyi praktykum z matematychnoi lohiky. Vinnytsia: VNTU, 117.
  19. Riznyk, V., Solomko, M. (2018). Minimization of conjunctive normal forms of boolean functions by combinatorial method. Technology Audit and Production Reserves, 5 (2 (43)), 42–55. https://doi.org/10.15587/2312-8372.2018.146312
  20. Ritsar, B. E. (1997). Metod minimizatsii bulevyh funktsiy. Problemy upravleniya i informatiki, 3, 100–113.
  21. Cheng, D. (2005). Semi-tensor Product of Matrices and its Applications to Dynamic Systems. New Directions and Applications in Control Theory, 61–79. https://doi.org/10.1007/10984413_5
  22. Feng, J., Zhao, R., Cui, Y. (2022). Simplification of logical functions with application to circuits. Electronic Research Archive, 30 (9), 3320–3336. https://doi.org/10.3934/era.2022168
  23. Cortadella, J. (2003). Timing-driven logic bi-decomposition. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 22 (6), 675–685. https://doi.org/10.1109/tcad.2003.811447
  24. Mishchenko, A., Steinbach, B., Perkowski, M. (2001). An algorithm for bi-decomposition of logic functions. Proceedings of the 38th Conference on Design Automation - DAC ’01, 103–108. https://doi.org/10.1145/378239.378353
  25. Chang S.-C., Marek-Sadowdka, M., Hwang, T. (1996). Technology mapping for TLU FPGAs based on decomposition of binary decision diagrams. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 15 (10), 1226–1236. https://doi.org/10.1109/43.541442
  26. Pottosin, Yu. V. (2022). Synthesis of combinational circuits by means of bi-decomposition of Boolean functions. Informatics, 19 (1), 7–18. https://doi.org/10.37661/1816-0301-2022-19-1-7-18
  27. Solomko, M., Batyshkina, I., Khomiuk, N., Ivashchuk, Y., Shevtsova, N. (2021). Developing the minimization of a polynomial normal form of boolean functions by the method of figurative transformations. Eastern-European Journal of Enterprise Technologies, 2 (4 (110)), 22–37. https://doi.org/10.15587/1729-4061.2021.229786
  28. Minziuk, V. (2023). Method of minimizing boolean functions for designing digital combinational circuits. Information and Communication Technologies, Electronic Engineering, 3 (1), 146–153. https://doi.org/10.23939/ictee2023.01.146
  29. Solomko, M., Khomiuk, N., Ivashchuk, Y., Nazaruk, V., Reinska, V., Zubyk, L., Popova, A. (2020). Implementation of the method of image transformations for minimizing the Sheffer functions. Eastern-European Journal of Enterprise Technologies, 5 (4 (107)), 19–34. https://doi.org/10.15587/1729-4061.2020.214899
  30. Solomko, M. (2021). Developing an algorithm to minimize boolean functions for the visual-matrix form of the analytical method. Eastern-European Journal of Enterprise Technologies, 1 (4 (109)), 6–21. https://doi.org/10.15587/1729-4061.2021.225325
  31. Riznyk, V., Solomko, M., Tadeyev, P., Nazaruk, V., Zubyk, L., Voloshyn, V. (2020). The algorithm for minimizing Boolean functions using a method of the optimal combination of the sequence of figurative transformations. Eastern-European Journal of Enterprise Technologies, 3 (4 (105)), 43–60. https://doi.org/10.15587/1729-4061.2020.206308
  32. Solomko, M., Tadeyev, P., Zubyk, L., Babych, S., Mala, Y., Voitovych, O. (2021). Implementation of the method of figurative transformations to minimizing symmetric Boolean functions. Eastern-European Journal of Enterprise Technologies, 4 (4 (112)), 23–39. https://doi.org/10.15587/1729-4061.2021.239149
Implementation of a non-standard system for simplifying Peirce-Webb functions

Downloads

Published

2024-10-31

How to Cite

Solomko, M., Tadeyev, P., Antoniuk, M., Mala, Y., Babych, S., & Ivashchuk, Y. (2024). Implementation of a non-standard system for simplifying Peirce-Webb functions. Eastern-European Journal of Enterprise Technologies, 5(4 (131), 6–32. https://doi.org/10.15587/1729-4061.2024.312968

Issue

Vol. 5 No. 4 (131) (2024): Mathematics and Cybernetics - applied aspects

Section

Mathematics and Cybernetics - applied aspects

License

Copyright (c) 2024 Mykhailo Solomko, Petro Tadeyev, Mykola Antoniuk, Yuliia Mala, Stepaniia Babych, Yakiv Ivashchuk

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.

A license agreement is a document in which the author warrants that he/she owns all copyright for the work (manuscript, article, etc.).
The authors, signing the License Agreement with TECHNOLOGY CENTER PC, have all rights to the further use of their work, provided that they link to our edition in which the work was published.
According to the terms of the License Agreement, the Publisher TECHNOLOGY CENTER PC does not take away your copyrights and receives permission from the authors to use and dissemination of the publication through the world's scientific resources (own electronic resources, scientometric databases, repositories, libraries, etc.).
In the absence of a signed License Agreement or in the absence of this agreement of identifiers allowing to identify the identity of the author, the editors have no right to work with the manuscript.
It is important to remember that there is another type of agreement between authors and publishers – when copyright is transferred from the authors to the publisher. In this case, the authors lose ownership of their work and may not use it in any way.