Determining the dynamic indicators of the pneumatic spring for high-speed rolling stock in the zone of a rail joint along a railroad track

Authors

DOI:

https://doi.org/10.15587/1729-4061.2024.315183

Keywords:

joint of railroad rails, pneumatic spring, high-speed rolling stock, acceleration of the rubber cord shell, deformations of the spring, natural frequency of spring oscillations

Abstract

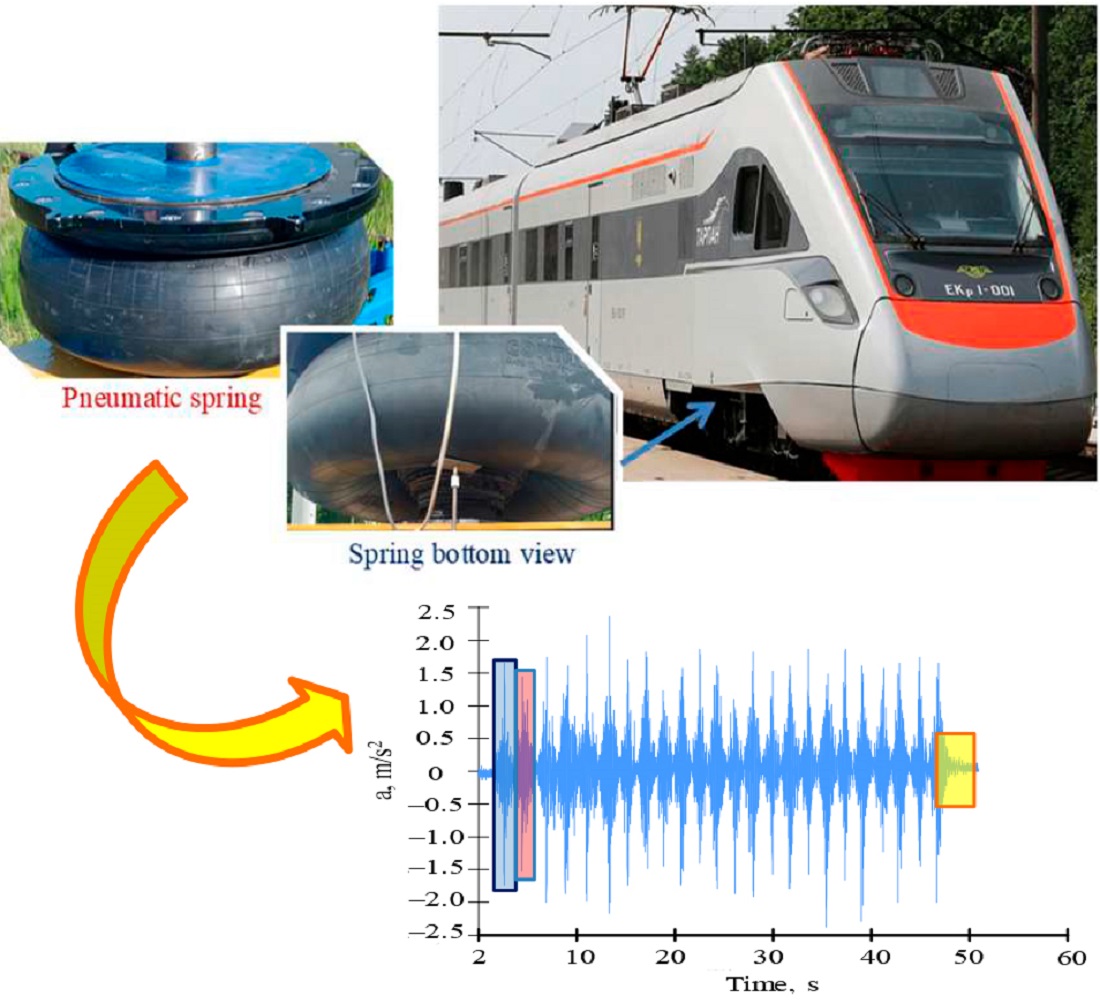
The object of this study is the pneumatic spring of the high-speed railroad rolling stock that moves over the rail joint of a railroad track with a vertical ledge.

The task solved was establishing the dynamic behavior of the rubber cord shell of the pneumatic spring of the high-speed railroad rolling stock, taking into account the design features of the railroad track, namely the rail joint.

The methodology for experimental testing of the pneumatic spring of the high-speed railroad rolling stock using the proposed dynamic test installation is given. Experimental tests of the pneumatic spring were carried out within the rail joint of the railroad track, which has a vertical ledge of 7.0 mm. It was established that the maximum value of the accelerations of the rubber cord shell of the pneumatic spring occurs in the vertical plane. The maximum vertical accelerations of the rubber cord shell of the pneumatic spring were 2.4 m/s2, horizontal transverse accelerations – 0.85 m/s2, and horizontal longitudinal accelerations – 0.9 m/s2.

It was determined that the deformations of the pneumatic spring in the vertical plane are higher than the deformations in the horizontal plane. The value of the maximum vertical deformations of the pneumatic spring was 4.1 mm, while the maximum value of horizontal deformations was 1.2 mm.

The natural frequencies and logarithmic decrements of oscillations damping were determined based on the obtained records of the free oscillations of the rubber cord shell of the pneumatic spring. It was established that the value of the first natural frequency of oscillations of the pneumatic spring is 3.21 Hz.

The logarithmic decrement of oscillation damping of the rubber cord shell of the pneumatic spring was determined based on the constructed graph of oscillation damping with an approximating exponent. It is 0.2147.

The obtained values of the dynamic indicators of the new pneumatic spring could be used in the future to control changes in the physical and mechanical properties of the rubber cord shell of the pneumatic spring under the operational conditions of the railroad track. In practice, engineers and scientists will be able to take into account the obtained dynamic parameters of the spring when designing and improving the pneumatic spring for high-speed train movement

Author Biographies

Andrii Kuzyshyn, Lviv Polytechnic National University

Doctor of Philosophy

Department of Railway Transport

Vitalii Kovalchuk, Lviv Polytechnic National University

Doctor of Technical Sciences, Professor

Department of Railway Transport

Yuriy Royko, Lviv Polytechnic National University

PhD, Associate Professor, Head of Department

Department of Transport Technologies

Yuliia Hermaniuk, Lviv Polytechnic National University

PhD, Associate Professor

Department of Transport Technologies

Yuriy Tereshchak, Lviv Research Institute for Forensic Expertise

PhD, Forensic Expert

Andrii Pulariia, Ukrainian State University of Science and Technologies

PhD, Associate Professor

Department of Wagons and Wagon Management

References

  1. Kuzyshyn, A., Batig, A., Kostritsa, S., Sobolevska, J., Kovalchuk, V., Dovhanyuk, S., Voznyak, O. (2018). Research of safety indicators of diesel train movement with two-stage spring suspension. MATEC Web of Conferences, 234, 05003. https://doi.org/10.1051/matecconf/201823405003
  2. Kuzyshyn, A., Batig, A., Kostritsa, S., Sobolevska, J., Dovhaniuk, S., Dzhus, V. (2020). Study of the dynamic behavior of rolling stock using a computer experiment. IOP Conference Series: Materials Science and Engineering, 985 (1), 012002. https://doi.org/10.1088/1757-899x/985/1/012002
  3. Kuzyshyn, A., Sobolevska, J., Kostritsa, S., Batig, A., Boiarko, V. (2023). Mathematical modeling of the second stage of spring suspension of high-speed rolling stock. AIP Conference Proceedings, 2684, 020007. https://doi.org/10.1063/5.0120402
  4. Kuzyshyn, A., Kostritsa, S., Ursulyak, L., Batig, A., Sobolevska, J., Voznyak, O. (2019). Research of the impact of geometric unevenness of the railway track on the dynamic parameters of the railway rolling stock with two-stage spring suspension. IOP Conference Series: Materials Science and Engineering, 664 (1), 012024. https://doi.org/10.1088/1757-899x/664/1/012024
  5. Alonso, A., Giménez, J. G., Nieto, J., Vinolas, J. (2010). Air suspension characterisation and effectiveness of a variable area orifice. Vehicle System Dynamics, 48, 271–286. https://doi.org/10.1080/00423111003731258
  6. Xu, L. (2020). Mathematical Modeling and Characteristic Analysis of the Vertical Stiffness for Railway Vehicle Air Spring System. Mathematical Problems in Engineering, 2020, 1–12. https://doi.org/10.1155/2020/2036563
  7. Sayyaadi, H., Shokouhi, N. (2010). Effects of air reservoir volume and connecting pipes' length and diameter on the air spring behavior inrail–vehicles. Iranian Journal of Science & Technology, Transaction B: Engineering, 34 (B5), 499–508. Available at: https://ijstm.shirazu.ac.ir/article_916.html
  8. Sayyaadi, H., Shokouhi, N. (2009). Improvement of passengers ride comfort in rail vehicles equipped with air springs. World Academy of Science, Engineering and Technology, 53, 827–833. Available at: https://citeseerx.ist.psu.edu/document?repid=rep1&type=pdf&doi=519a6631377f3334f9e80d6b02df0ab15b87c024
  9. Sayyaadi, H., Shokouhi, N. (2009). New dynamics model for rail vehicles and optimizing air suspension parameters using GA. International Jurnal of Science & Technology, 16 (6), 496–512. Available at: https://scientiairanica.sharif.edu/article_3135.html
  10. Jin, X., Wen, Z., Wang, K., Xiao, X. (2006). Effect of passenger car curving on rail corrugation at a curved track. Wear, 260 (6), 619–633. https://doi.org/10.1016/j.wear.2005.03.016
  11. Jin, X. S., Wen, Z. F. (2008). Effect of discrete track support by sleepers on rail corrugation at a curved track. Journal of Sound and Vibration, 315 (1-2), 279–300. https://doi.org/10.1016/j.jsv.2008.01.057
  12. Chen, J.-J., Yin, Z.-H., Rakheja, S., He, J.-H., Guo, K.-H. (2017). Theoretical modelling and experimental analysis of the vertical stiffness of a convoluted air spring including the effect of the stiffness of the bellows. Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering, 232 (4), 547–561. https://doi.org/10.1177/0954407017704589
  13. Facchinetti, A., Mazzola, L., Alfi, S., Bruni, S. (2010). Mathematical modelling of the secondary airspring suspension in railway vehicles and its effect on safety and ride comfort. Vehicle System Dynamics, 48, 429–449. https://doi.org/10.1080/00423114.2010.486036
  14. Gao, H. X., Chi, M. R., Zhu, M. H., Wu, P. B. (2013). Study on Different Connection Types of Air Spring. Applied Mechanics and Materials, 423-426, 2026–2034. https://doi.org/10.4028/www.scientific.net/amm.423-426.2026
  15. Li, X., Li, T. (2013). Research on vertical stiffness of belted air springs. Vehicle System Dynamics, 51 (11), 1655–1673. https://doi.org/10.1080/00423114.2013.819984
  16. Li, X., He, Y., Liu, W., Wei, Y. (2015). Research on the vertical stiffness of a rolling lobe air spring. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 230 (4), 1172–1183. https://doi.org/10.1177/0954409715585370
  17. Mazzola, L., Berg, M. (2012). Secondary suspension of railway vehicles - air spring modelling: Performance and critical issues. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 228 (3), 225–241. https://doi.org/10.1177/0954409712470641
  18. Nakajima, T., Shimokawa, Y., Mizuno, M., Sugiyama, H. (2014). Air Suspension System Model Coupled With Leveling and Differential Pressure Valves for Railroad Vehicle Dynamics Simulation. Journal of Computational and Nonlinear Dynamics, 9 (3). https://doi.org/10.1115/1.4026275
  19. Tanaka, T., Sugiyama, H. (2019). Prediction of railway wheel load unbalance induced by air suspension leveling valves using quasi-steady curve negotiation analysis procedure. Proceedings of the Institution of Mechanical Engineers, Part K: Journal of Multi-Body Dynamics, 234 (1), 19–37. https://doi.org/10.1177/1464419319867179
  20. Nieto, A. J., Morales, A. L., González, A., Chicharro, J. M., Pintado, P. (2008). An analytical model of pneumatic suspensions based on an experimental characterization. Journal of Sound and Vibration, 313 (1-2), 290–307. https://doi.org/10.1016/j.jsv.2007.11.027
  21. Kuzyshyn, A., Kovalchuk, V., Sobolevska, Y., Royko, Y., Kravets, I. (2024). Determining the effect of additional tank volume and air pressure in the spring on the dynamic indicators of a pneumatic system of spring suspension in high-speed railroad rolling stock. Eastern-European Journal of Enterprise Technologies, 3 (7 (129)), 47–62. https://doi.org/10.15587/1729-4061.2024.304051
  22. Kuzyshyn, A., Kovalchuk, V., Stankevych, V., Hilevych, V. (2023). Determining patterns in the influence of the geometrical parameters of the connecting pipeline on the dynamic parameters of the pneumatic spring of railroad rolling stock. Eastern-European Journal of Enterprise Technologies, 1 (7 (121)), 57–65. https://doi.org/10.15587/1729-4061.2023.274180
  23. Zhu, H., Yang, J., Zhang, Y., Feng, X. (2017). A novel air spring dynamic model with pneumatic thermodynamics, effective friction and viscoelastic damping. Journal of Sound and Vibration, 408, 87–104. https://doi.org/10.1016/j.jsv.2017.07.015
  24. Qi, Z., Li, F., Yu, D. (2016). A three-dimensional coupled dynamics model of the air spring of a high-speed electric multiple unit train. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 231 (1), 3–18. https://doi.org/10.1177/0954409715620534
  25. Xu, L. (2014). Research on nonlinear modeling and dynamic characteristics of lateral stiffness of vehicle air spring system. Advances in Mechanical Engineering, 12 (6). https://doi.org/10.1177/1687814020930457
  26. Redchenko, V. P. (2014). Analysis of dynamic testing of bridges using the program "SPECTRUM". Mosty ta tuneli: teoriya, doslidzhennia, praktyka, 6, 119–125. Available at: http://nbuv.gov.ua/UJRN/Mttdp_2014_6_17
  27. Kuzyshyn, A. Ya., Kovalchuk, V. V., Kostiv, N. V. (2024). Investigation of the Influence of a Turnout Cross on Vertical and Horizontal Deformations of a Pneumatic Spring of High-Speed Rolling Stock. Science and Transport Progress, 3 (107), 63–72. https://doi.org/10.15802/stp2024/312930
Determining the dynamic indicators of the pneumatic spring for high-speed rolling stock in the zone of a rail joint along a railroad track

Downloads

Published

2024-12-27

How to Cite

Kuzyshyn, A., Kovalchuk, V., Royko, Y., Hermaniuk, Y., Tereshchak, Y., & Pulariia, A. (2024). Determining the dynamic indicators of the pneumatic spring for high-speed rolling stock in the zone of a rail joint along a railroad track. Eastern-European Journal of Enterprise Technologies, 6(7 (132), 65–74. https://doi.org/10.15587/1729-4061.2024.315183

Issue

Vol. 6 No. 7 (132) (2024): Applied mechanics

Section

Applied mechanics

License

Copyright (c) 2024 Andrii Kuzyshyn, Vitalii Kovalchuk, Yuriy Royko, Yuliia Hermaniuk, Yuriy Tereshchak, Andrii Pulariia

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.

A license agreement is a document in which the author warrants that he/she owns all copyright for the work (manuscript, article, etc.).
The authors, signing the License Agreement with TECHNOLOGY CENTER PC, have all rights to the further use of their work, provided that they link to our edition in which the work was published.
According to the terms of the License Agreement, the Publisher TECHNOLOGY CENTER PC does not take away your copyrights and receives permission from the authors to use and dissemination of the publication through the world's scientific resources (own electronic resources, scientometric databases, repositories, libraries, etc.).
In the absence of a signed License Agreement or in the absence of this agreement of identifiers allowing to identify the identity of the author, the editors have no right to work with the manuscript.
It is important to remember that there is another type of agreement between authors and publishers – when copyright is transferred from the authors to the publisher. In this case, the authors lose ownership of their work and may not use it in any way.