Виявлення мережевих спільнот за допомогою модифікованого критерію модулярності
DOI:
https://doi.org/10.15587/1729-4061.2024.318452Ключові слова:
модулярність мереж, спільноти вузлів, розбиття мереж, асортативність, задачі великої розмірностіАнотація
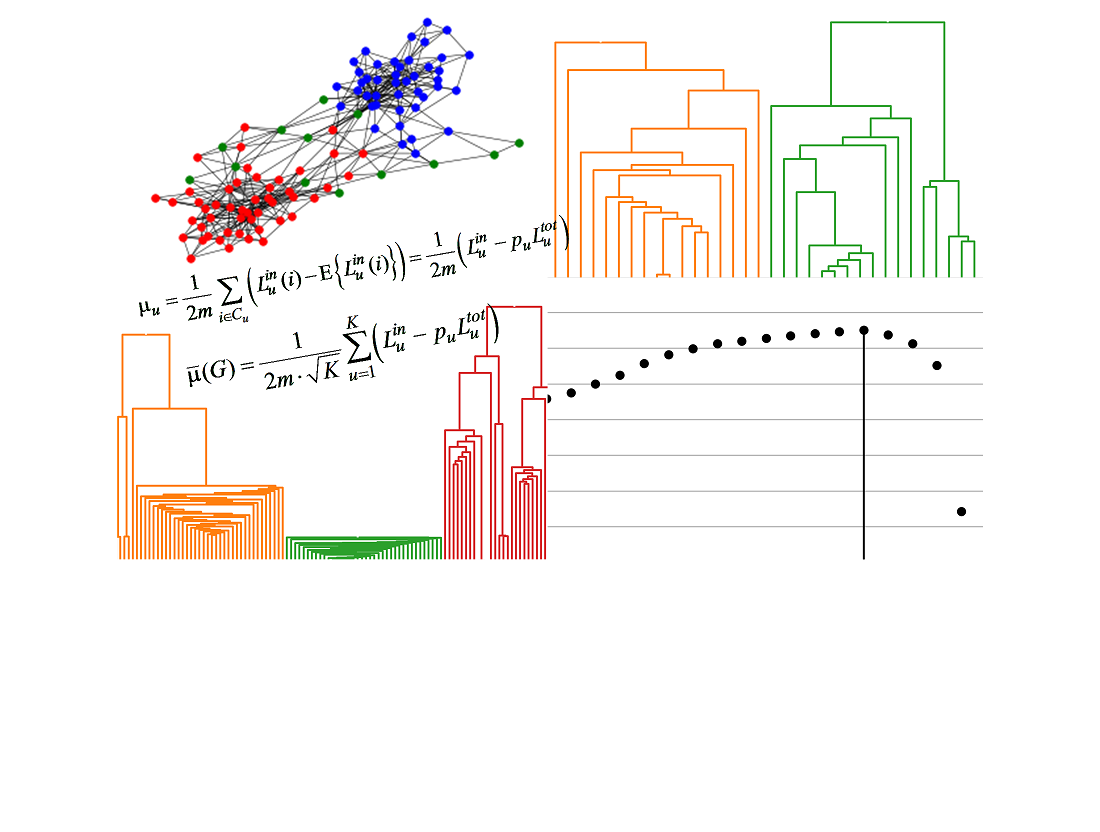
Об’єктом досліджень є складні мережі, моделлю яких є неорієнтовані зважені звичайні (без петель та кратних ребер) графи. Розглядається проблема визначення спільнот, тобто розбиття множини вузлів мережі спільноти. При цьому вважається, що такі спільноти повинні бути такими, що попарно не перетинаються. Наразі існує багато підходів до вирішення цієї проблеми та, відповідно, багато методів, які її реалізують. Розглядаються методи, які грунтуються на максимізації функції модулярності мережі. Запропоновано модифікований критерій (функцію) модулярності. Значення цього критерію явним чином залежить від кількості вузлів у спільнотах. Розбиття вузлів мережі на спільноти з максимізацією за таким критерієм є суттєво більш схильним до виділення малих спільнот, або навіть одноосібних вузлів. Ця властивість є визначальною характеристикою запропонованого метода та є корисною у разі, якщо мережа, яка аналізується, дійсно має малі спільноти. Крім того, запропонований критерій модулярності є нормованим відносно поточної кількості спільнот. Це дає змогу порівнювати між собою модулярність розбиттів мережі на різну кількість спільнот. Це, в свою чергу, дає змогу оцінити кількість спільнот, які формуються, у тих випадках, коли ця кількість апріорі невідома. Розроблено метод розбиття вузлів мережі на спільноти за критерієм максимуму модулярності. Відповідний алгоритм є субоптимальним, відноситься до класу жадібних, та має низьку обчислювальну складність – лінійну відносно кількості вузлів мережі. Внаслідок цього він є швидким, тому може застосовуватись для розбиття мереж на спільноти. Проведене тестування розробленого методу виявлення мережевих спільнот на класичних датасетах, яке підтвердило ефективність запропонованого підходу
Посилання
- Newman, M. E. J. (2003). Mixing patterns in networks. Physical Review E, 67 (2). https://doi.org/10.1103/physreve.67.026126
- Cinelli, M., Peel, L., Iovanella, A., Delvenne, J.-C. (2020). Network constraints on the mixing patterns of binary node metadata. Physical Review E, 102 (6). https://doi.org/10.1103/physreve.102.062310
- Hamdaqa, M., Tahvildari, L., LaChapelle, N., Campbell, B. (2014). Cultural scene detection using reverse Louvain optimization. Science of Computer Programming, 95, 44–72. https://doi.org/10.1016/j.scico.2014.01.006
- Girvan, M., Newman, M. E. J. (2002). Community structure in social and biological networks. Proceedings of the National Academy of Sciences, 99 (12), 7821–7826. https://doi.org/10.1073/pnas.122653799
- Pascual‐García, A., Bell, T. (2020). functionInk: An efficient method to detect functional groups in multidimensional networks reveals the hidden structure of ecological communities. Methods in Ecology and Evolution, 11 (7), 804–817. https://doi.org/10.1111/2041-210x.13377
- Newman, M. E. J. (2004). Detecting community structure in networks. The European Physical Journal B - Condensed Matter, 38 (2), 321–330. https://doi.org/10.1140/epjb/e2004-00124-y
- Karrer, B., Newman, M. E. J. (2011). Stochastic blockmodels and community structure in networks. Physical Review E, 83 (1). https://doi.org/10.1103/physreve.83.016107
- Cohen-Addad, V., Kosowski, A., Mallmann-Trenn, F., Saulpic, D. (2020). On the Power of Louvain in the Stochastic Block Model. Advances in Neural Information Processing Systems (NeurIPS 2020). Vancourer, 4055–4066. Available at: https://hal.science/hal-03140367
- Newman, M. E. J. (2006). Modularity and community structure in networks. Proceedings of the National Academy of Sciences, 103 (23), 8577–8582. https://doi.org/10.1073/pnas.0601602103
- Blondel, V. D., Guillaume, J.-L., Lambiotte, R., Lefebvre, E. (2008). Fast unfolding of communities in large networks. Journal of Statistical Mechanics: Theory and Experiment, 2008 (10), P10008. https://doi.org/10.1088/1742-5468/2008/10/p10008
- Raskin, L., Sira, O. (2021). Devising methods for planning a multifactorial multilevel experiment with high dimensionality. Eastern-European Journal of Enterprise Technologies, 5 (4 (113)), 64–72. https://doi.org/10.15587/1729-4061.2021.242304
- Fortunato, S., Barthélemy, M. (2007). Resolution limit in community detection. Proceedings of the National Academy of Sciences, 104 (1), 36–41. https://doi.org/10.1073/pnas.0605965104
- Orgnet. Available at: http://www.orgnet.com/
- Piraveenan, M., Prokopenko, M., Zomaya, A. Y. (2012). On congruity of nodes and assortative information content in complex networks. Networks and Heterogeneous Media, 7 (3), 441–461. https://doi.org/10.3934/nhm.2012.7.441
- Shergin, V., Udovenko, S., Chala, L. (2020). Assortativity Properties of Barabási-Albert Networks. Data-Centric Business and Applications, 55–66. https://doi.org/10.1007/978-3-030-43070-2_4
- Shergin, V., Chala, L., Udovenko, S. (2019). Assortativity Properties of Scale-Free Networks. 2019 IEEE International Scientific-Practical Conference Problems of Infocommunications, Science and Technology (PIC S&T), 723–726. https://doi.org/10.1109/picst47496.2019.9061369
- Shergin, V., Chala, L., Udovenko, S., Pohurska, M. (2018). Assortativity of an elastic network with implicit use of information about nodes degree. CEUR Workshop Proceedings, 131–140. Available at: https://ceur-ws.org/Vol-3018/Paper_12.pdf
- Noldus, R., Van Mieghem, P. (2015). Assortativity in complex networks. Journal of Complex Networks, 3 (4), 507–542. https://doi.org/10.1093/comnet/cnv005
- Network data. Available at: https://public.websites.umich.edu/~mejn/netdata/
##submission.downloads##
Опубліковано
Як цитувати
Номер
Розділ
Ліцензія
Авторське право (c) 2024 Vadim Shergin, Sergiy Grinyov, Larysa Chala, Serhii Udovenko

Ця робота ліцензується відповідно до Creative Commons Attribution 4.0 International License.
Закріплення та умови передачі авторських прав (ідентифікація авторства) здійснюється у Ліцензійному договорі. Зокрема, автори залишають за собою право на авторство свого рукопису та передають журналу право першої публікації цієї роботи на умовах ліцензії Creative Commons CC BY. При цьому вони мають право укладати самостійно додаткові угоди, що стосуються неексклюзивного поширення роботи у тому вигляді, в якому вона була опублікована цим журналом, але за умови збереження посилання на першу публікацію статті в цьому журналі.
Ліцензійний договір – це документ, в якому автор гарантує, що володіє усіма авторськими правами на твір (рукопис, статтю, тощо).
Автори, підписуючи Ліцензійний договір з ПП «ТЕХНОЛОГІЧНИЙ ЦЕНТР», мають усі права на подальше використання свого твору за умови посилання на наше видання, в якому твір опублікований. Відповідно до умов Ліцензійного договору, Видавець ПП «ТЕХНОЛОГІЧНИЙ ЦЕНТР» не забирає ваші авторські права та отримує від авторів дозвіл на використання та розповсюдження публікації через світові наукові ресурси (власні електронні ресурси, наукометричні бази даних, репозитарії, бібліотеки тощо).
За відсутності підписаного Ліцензійного договору або за відсутністю вказаних в цьому договорі ідентифікаторів, що дають змогу ідентифікувати особу автора, редакція не має права працювати з рукописом.
Важливо пам’ятати, що існує і інший тип угоди між авторами та видавцями – коли авторські права передаються від авторів до видавця. В такому разі автори втрачають права власності на свій твір та не можуть його використовувати в будь-який спосіб.










