Construction of adaptive inventory management models for a trading enterprise under unstable conditions
DOI:
https://doi.org/10.15587/1729-4061.2025.336050Keywords:
random demand, changes in operating activity characteristics, inventory replenishment, operating effectAbstract
This study’s object is the inventory management processes at a retail enterprise under conditions of random fluctuations in demand. The findings are aimed at solving the task related to the complexity in determining the optimal volumes of goods purchases under unstable conditions. As alternatives, it is proposed to consider two policies for replenishing stocks – the policy of a minimum stock of goods and the policy of a permanent reserve stock taking into account the possibility of transferring unsatisfied demand.
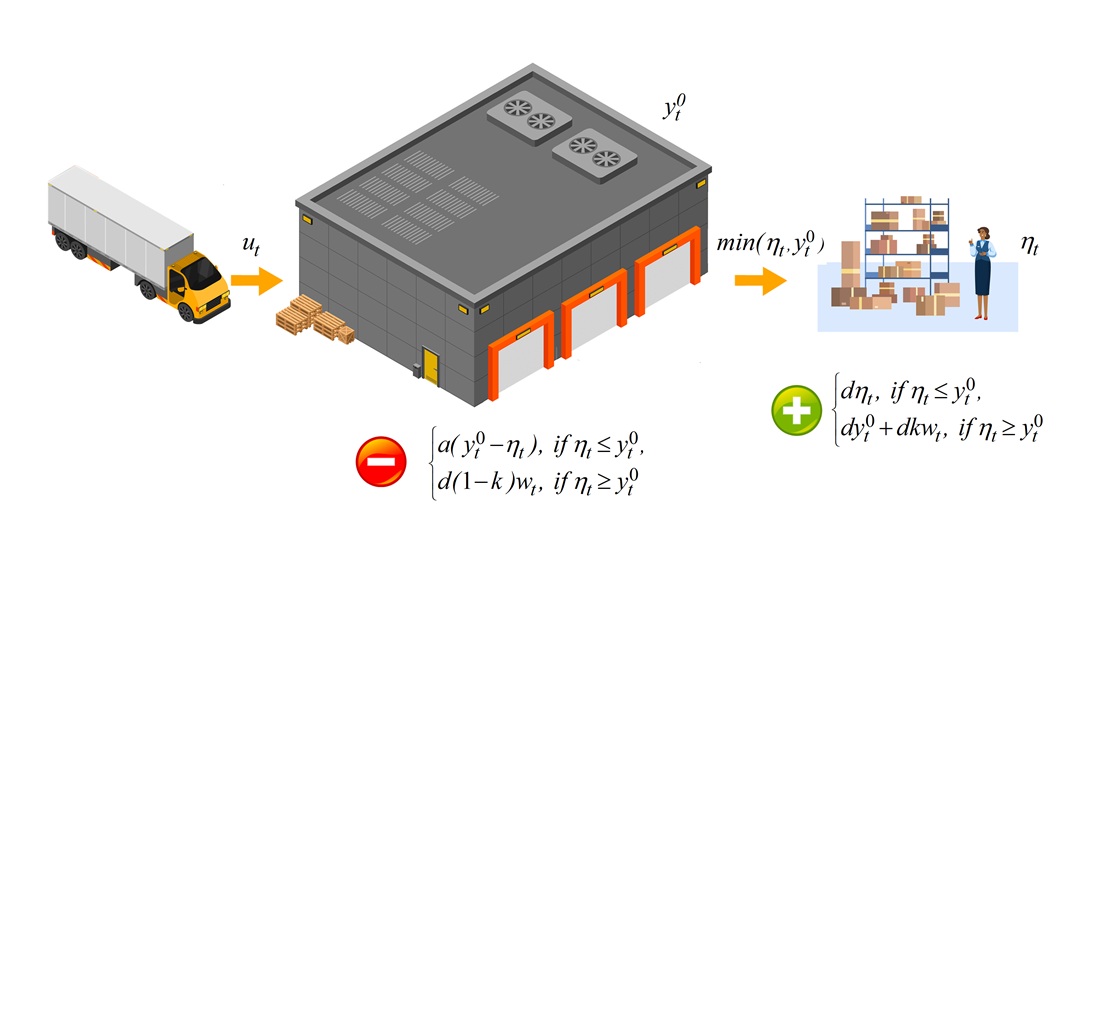
Each policy is estimated by the value of the expected operating effect, which takes into account the income from the sale of goods and losses from the storage of unsold goods or from unsatisfied demand. The hypothesis put forward assumes that the value of the expected operating effect of each policy could be calculated depending on parameters for the law of the probability distribution of demand volumes and on the economic characteristics of the situation.
A model of dependence of the expected operating effect on the volumes of purchases and the parameters of the normal probability distribution functions of demand has been built. Mathematical expressions for the expected operating effect for the two policies under analysis have been derived. A comparative analysis of the effectiveness of these policies was conducted, which made it possible to identify the zones of values of the indicators of the choice situation for which a certain policy is the best. Under certain conditions, the expected operational effect for an arbitrarily chosen policy could reach only 70% of the operational effect corresponding to the best policy. This proves the ability of adaptive management to improve the operational effect as well as its economic efficiency
References
- Retail trade volume index overview. Eurostat. Available at: https://ec.europa.eu/eurostat/statistics-explained/index.php?title=Retail_trade_volume_index_overview
- Share of value added to the gross domestic product of the United States in 2024, by industry. Statista. Available at: https://www.statista.com/statistics/248004/percentage-added-to-the-us-gdp-by-industry/
- Vyrobnytstvo ta rozpodil valovoho vnutrishnoho produktu za vydamy ekonomichnoi diyalnosti. Derzhavna sluzhba Ukrainy. Available at: https://www.ukrstat.gov.ua/operativ/operativ2008/vvp/vvp_ric/arh_vtr_u.htm
- Ziukov, S. (2015). A literature review on models of inventory management under uncertainty. Business Systems & Economics, 5 (1), 26. https://doi.org/10.13165/vse-15-5-1-03
- San-José, L. A., Sicilia, J., González-de-la-Rosa, M., Febles-Acosta, J. (2021). Profit maximization in an inventory system with time-varying demand, partial backordering and discrete inventory cycle. Annals of Operations Research, 316 (2), 763–783. https://doi.org/10.1007/s10479-021-04161-6
- Pando, V., San-José, L. A., Sicilia, J., Alcaide-López-de-Pablo, D. (2024). An inventory model with price- and stock-dependent demand and time- and stock quantity-dependent holding cost under profitability maximization. Computers & Operations Research, 164, 106520. https://doi.org/10.1016/j.cor.2023.106520
- Silver, E. A., Pyke, D. F., Thomas, D. J. (2016). Inventory and Production Management in Supply Chains. CRC Press. https://doi.org/10.1201/9781315374406
- Becerra, P., Mula, J., Sanchis, R. (2021). Green supply chain quantitative models for sustainable inventory management: A review. Journal of Cleaner Production, 328, 129544. https://doi.org/10.1016/j.jclepro.2021.129544
- Žic, J., Žic, S., Đukić, G. (2024). Quantitative Assessment of Green Inventory Management in Supply Chains: Simulation-Based Study of Economic and Environmental Outcomes Aligned with ISO 14083 Standard. Applied Sciences, 14 (20), 9507. https://doi.org/10.3390/app14209507
- Violi, A., Laganá, D., Paradiso, R. (2019). The inventory routing problem under uncertainty with perishable products: an application in the agri-food supply chain. Soft Computing, 24 (18), 13725–13740. https://doi.org/10.1007/s00500-019-04497-z
- Sun, Y., Qiu, R., Sun, M. (2024). Robust pricing and inventory decisions in ship‐from‐store omnichannel operations. Managerial and Decision Economics, 46 (1), 5–20. https://doi.org/10.1002/mde.4348
- Girija Bai, H., Mohamed Ismail, A., Kaviya, D., Muniappan, P. (2021). An EOQ model for deteriorating products with backorder and fixed transportation cost. Journal of Physics: Conference Series, 1770 (1), 012100. https://doi.org/10.1088/1742-6596/1770/1/012100
- Rahman, M. S., Das, S., Manna, A. K., Shaikh, A. A., Bhunia, A. K., Cárdenas-Barrón, L. E. et al. (2021). A Mathematical Model of the Production Inventory Problem for Mixing Liquid Considering Preservation Facility. Mathematics, 9 (24), 3166. https://doi.org/10.3390/math9243166
- Das, R., Barman, A., De, P. K. (2021). Integration of pricing and inventory decisions of deteriorating item in a decentralized supply chain: a Stackelberg-game approach. International Journal of System Assurance Engineering and Management, 13 (1), 479–493. https://doi.org/10.1007/s13198-021-01299-1
- Cárdenas-Barrón, L. E., Mandal, B., Sicilia, J., San-José, L. A., Abdul-Jalbar, B. (2021). Optimizing price, order quantity, and backordering level using a nonlinear holding cost and a power demand pattern. Computers & Operations Research, 133, 105339. https://doi.org/10.1016/j.cor.2021.105339
- Pervin, M., Roy, S. K., Sannyashi, P., Weber, G.-W. (2023). Sustainable inventory model with environmental impact for non-instantaneous deteriorating items with composite demand. RAIRO - Operations Research, 57 (1), 237–261. https://doi.org/10.1051/ro/2023005
- Hariom, Sharma, K. C., Singh, K., Singh, D. (2024). Analysis of an inventory model for time-dependent linear demand rate three levels of production with shortage. International Journal of Professional Business Review, 9 (4), e04579. https://doi.org/10.26668/businessreview/2024.v9i4.4579
- Zaruba, V. Ya. (2017). Optimization of production plans according to estimates of the probability of future orders. Marketynh i menedzhment innovatsiy, 2, 222–232. Available at: https://mmi.sumdu.edu.ua/wp-content/uploads/mmi/volume-8-issue-2/mmi2017_2_222_232.pdf
- Zaruba, V., Parfentenko, I. (2020). Risk Management Models in Operative Planning at an Industrial Enterprise. 2020 IEEE International Conference on Problems of Infocommunications. Science and Technology (PIC S&T), 33–38. https://doi.org/10.1109/picst51311.2020.9467954
- Potrashkova, L., Zaruba, V., Guryanova, L., Sokol, K., Kuksa, I. (2022). Analysis of the policy of operation activity of an enterprise with product reservation. Eastern-European Journal of Enterprise Technologies, 1 (3 (115)), 31–42. https://doi.org/10.15587/1729-4061.2022.252667
Downloads
Published
How to Cite
Issue
Section
License
Copyright (c) 2025 Viktor Zaruba, Liudmyla Potrashkova, Oleksii Khoroshevskyi, Taras Chmeruk

This work is licensed under a Creative Commons Attribution 4.0 International License.
The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.
A license agreement is a document in which the author warrants that he/she owns all copyright for the work (manuscript, article, etc.).
The authors, signing the License Agreement with TECHNOLOGY CENTER PC, have all rights to the further use of their work, provided that they link to our edition in which the work was published.
According to the terms of the License Agreement, the Publisher TECHNOLOGY CENTER PC does not take away your copyrights and receives permission from the authors to use and dissemination of the publication through the world's scientific resources (own electronic resources, scientometric databases, repositories, libraries, etc.).
In the absence of a signed License Agreement or in the absence of this agreement of identifiers allowing to identify the identity of the author, the editors have no right to work with the manuscript.
It is important to remember that there is another type of agreement between authors and publishers – when copyright is transferred from the authors to the publisher. In this case, the authors lose ownership of their work and may not use it in any way.








