Developing a method of accounting for the existence of local surface heat exchange in rods of variable cross-section
DOI:
https://doi.org/10.15587/1729-4061.2023.273635Keywords:
heat flux intensity, thermal conductivity coefficient, temperature, heat transfer coefficientAbstract
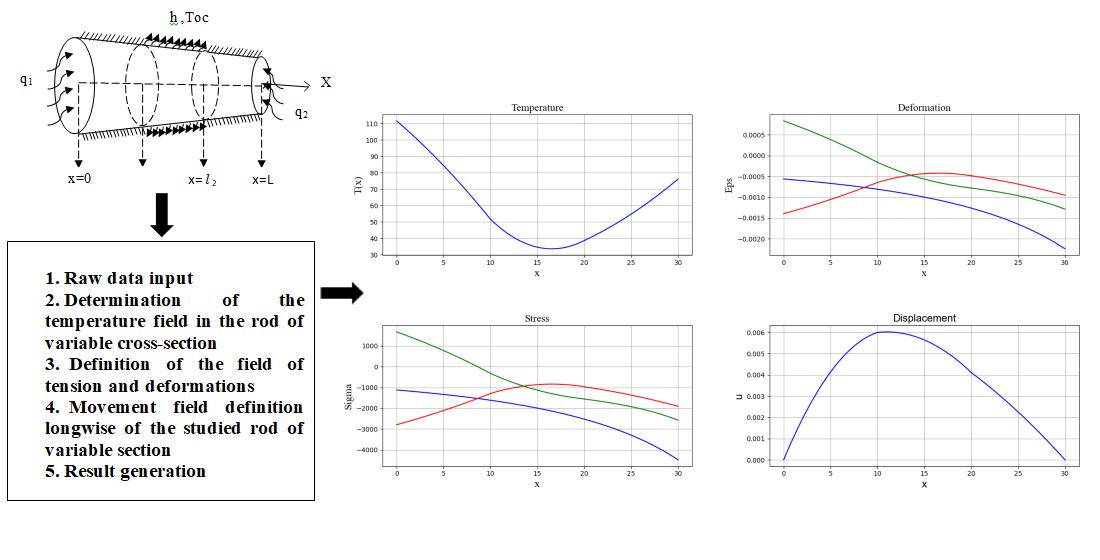
The load-bearing elements of a number of strategic equipment are of limited length and variable cross-section. Most of them are exposed to certain types of heat sources. In order to ensure the reliable operation of this equipment, it is necessary to know the temperature field along the length of the variable cross-section rod. In this paper, a computational algorithm and a method for determining the temperature field along the length of a rod with a limited length and variable cross-section are proposed. They are based on the fundamental laws of conservation of energy.
The nonlinearity of the process is due to nonlinear dependencies of the areas of the variable cross-section on the coordinate. The radius of the cross-section of the rod decreases linearly along the entire length, starting from the left end. The side surface of the first and third discrete elements of the rod is heat-insulated. Convective heat exchange with the environment takes place on the side surface of the second discrete element of the rod.
The cross-sectional area of the left end of the rod is under the heat flow with a constant intensity, and a heat flow with different intensities is supplied to the right end, wherein the heat transfer coefficient is considered constant. For this task, you must first determine the law of temperature distribution along the length of the rod. In addition, if one end is rigidly fixed and the other end is free, the elongation must be calculated depending on the available heat sources, the physical and geometric characteristics of the rod, taking into account the presence of insulation.
In case of pinching of both ends of the investigated rod, the value of axial compressive force is calculated taking into account the addition of real factors. The distribution of all components of the strain, stress, and displacement field is also defined
References
- Timoshenko, S., Goodier. J. N. (1951). Theory of Elasticity. New York. Available at: http://parastesh.usc.ac.ir/files/1538886893033.pdf
- Shorr, B. F. (2015). Thermoelasticity. Thermal Integrity in Mechanics and Engineering, 33–56. https://doi.org/10.1007/978-3-662-46968-2_2
- Banerjee, B. (2006). Basic Thermoelasticity. doi: http://dx.doi.org/10.13140/RG.2.1.1144.2005
- Saoud, S. (2009). Etude et Analyse Mathematique des Problems Non Lineaires Modelisant les Etats Thermiques d’un Superconducteur: Generalisation au Cas Tridimensionnel.
- Griffith, G., Tucker, S., Milsom, J., Stone, G. (2000). Problems with modern air-cooled generator stator winding insulation. IEEE Electrical Insulation Magazine, 16 (6), 6–10. doi: https://doi.org/10.1109/57.887599
- Li, Y. (2019). Investigation of Heat Transfer Characteristics on Rod Fastening Rotor. IOP Conference Series: Materials Science and Engineering, 677 (3), 032032. doi: https://doi.org/10.1088/1757-899x/677/3/032032
- Shibib, K., Minshid, M., Alattar, N. (2011). Thermal and stress analysis in Nd: YAG laser rod with different double end pumping methods. Thermal Science, 15, 399–407. doi: https://doi.org/10.2298/tsci101201004s
- Andreev, V., Turusov, R. (2016). Nonlinear modeling of the kinetics of thermal stresses in polymer rods. Advanced Materials and Structural Engineering, 719–722. doi: https://doi.org/10.1201/b20958-150
- Belytschko, T., Liu, W. K., Moran, B. (2000). Nonlinear Finite Elements for Continua and Structures. John Wiley and Sons.
- Wright, T. W. (2002). The Physics and Mathematics of Adiabatic Shear Bands. Cambridge University Press.
- Batra, R. C. (2006). Elements of Continuum Mechanics. AIAA. doi: https://doi.org/10.2514/4.861765
- Sukarno, D. H. (2021). Analysis of nuclear fuel rod temperature distribution using CFD calculation and analytical solution. PROCEEDINGS OF THE 6TH INTERNATIONAL SYMPOSIUM ON CURRENT PROGRESS IN MATHEMATICS AND SCIENCES 2020 (ISCPMS 2020). doi: https://doi.org/10.1063/5.0058888
- El-Azab, J. M., Kandel, H. M., Khedr, M. A., El-Ghandoor, H. M. (2014). Numerical Study of Transient Temperature Distribution in Passively Q-Switched Yb:YAG Solid-State Laser. Optics and Photonics Journal, 04 (03), 46–53. doi: https://doi.org/10.4236/opj.2014.43007
- Khany, S. E., Krishnan, K. N., Wahed, M. A. (2012). Study of Transient Temperature Distribution in a Friction Welding Process and its effects on its Joints. International Journal Of Computational Engineering Research, 2 (5), 1645.
- Mishchenko, A. (2020). Spatially Structure Spatial Problem of the Stressed-Deformed State of a Structural Inhomogeneous Rod. IOP Conference Series: Materials Science and Engineering, 953, 012004. doi: https://doi.org/10.1088/1757-899x/953/1/012004
- Hwang, J.-K. (2020). Thermal Behavior of a Rod during Hot Shape Rolling and Its Comparison with a Plate during Flat Rolling. Processes, 8 (3), 327. doi: https://doi.org/10.3390/pr8030327
- Logan, D. L. (2012). A First Course in the Finite Element Method. CENGAGE Learning, 727–764.
- Liu, Q., He, X. (2023). Thermal Analysis of Terfenol-D Rods with Different Structures. Micromachines, 14 (1), 216. doi: https://doi.org/10.3390/mi14010216
- Gaspar Jr., J. C. A., Moreira, M. L., Desampaio, P. A. B. (2011). Temperature Distribution on Fuel Rods: A study on the Effect of Eccentricity in the Position of UO2 Pellets. 20-th International Conference «Nuclear Energy for New Europe». Available at: https://arhiv.djs.si/proc/nene2011/pdf/814.pdf
Downloads
Published
How to Cite
Issue
Section
License
Copyright (c) 2023 Mukaddas Arshidinova, Azat Tashev, Anarbay Kudaykulov

This work is licensed under a Creative Commons Attribution 4.0 International License.
The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.
A license agreement is a document in which the author warrants that he/she owns all copyright for the work (manuscript, article, etc.).
The authors, signing the License Agreement with TECHNOLOGY CENTER PC, have all rights to the further use of their work, provided that they link to our edition in which the work was published.
According to the terms of the License Agreement, the Publisher TECHNOLOGY CENTER PC does not take away your copyrights and receives permission from the authors to use and dissemination of the publication through the world's scientific resources (own electronic resources, scientometric databases, repositories, libraries, etc.).
In the absence of a signed License Agreement or in the absence of this agreement of identifiers allowing to identify the identity of the author, the editors have no right to work with the manuscript.
It is important to remember that there is another type of agreement between authors and publishers – when copyright is transferred from the authors to the publisher. In this case, the authors lose ownership of their work and may not use it in any way.








