Знаходження аналітичного рішення для балістичного коефіцієнта розмагнічування циліндра за допомогою сферичних гармонік
DOI:
https://doi.org/10.15587/1729-4061.2024.301008Ключові слова:
балістичний коефіцієнт розмагнічування циліндра, індуктивна намагніченість, сферична гармоніка магнітного поляАнотація
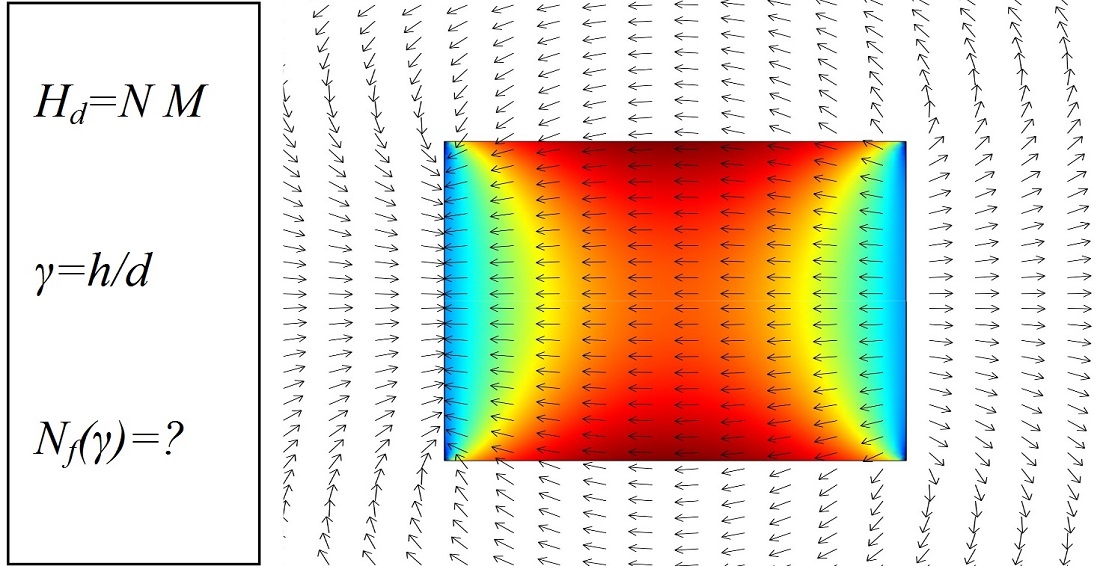
В роботі досліджується аналітичне рішення для розрахунку балістичного коефіцієнта розмагнічування магнетиків циліндричної форми при великих значеннях магнітної сприйнятливості і довільному значенні подовження. Застосування саме аналітичного рішення для розрахунку коефіцієнта розмагнічування суттєво спрощує моделювання та розрахунок магнітних характеристик технічних об'єктів циліндричної форми. Побудовано спрощену аналітичну модель скалярного потенціалу магнітного поля циліндра з нескінченною магнітною сприятливістю, індуктивно намагніченого в однорідному магнітному полі, застосовуючи наближене уявлення про розподіл фіктивних магнітних зарядів на його поверхні. Використано метод сферичного гармонічного аналізу для магнітного поля, що дозволило отримати аналітичне уявлення поля розмагнічування в центральному поперечному перерізі циліндра. Запропоновано обмеження гармонійного ряду цього представлення сімома першими гармоніками та застосовано додатковий амплітудний коефіцієнт для корекції внеску першої гармоніки в поле розмагнічування. Це дозволило компенсувати викривлення магнітного поля поблизу торців циліндра та наблизити спрощену аналітичну модель до цільової математичної моделі із однорідним магнітним полем розмагнічування. Виконано оцінку достовірності результатів розрахунку балістичного коефіцієнта розмагнічування за отриманою формулою шляхом їх порівняння з відомими результатами, отриманими за допомогою числового методу розрахунку та за емпіричними формулами. Показано, що запропонований підхід дозволяє отримувати достовірні з відхиленням до 5 % результати розрахунку балістичного коефіцієнта розмагнічування при нескінченній сприятливості в діапазоні значень подовження циліндра від 0.01 до 500
Посилання
- Rozenblat, M. A. (1954). Koeffitsienty razmagnichivaniya sterzhney vysokoy pronitsaemosti. Zhurnal tehnicheskoy fiziki, 4 (24), 637–661.
- Okoshi, T. (1965). Demagnetizing Factors of Rods and Tubes Computed from Analog Measurements. Journal of Applied Physics, 36 (8), 2382–2387. https://doi.org/10.1063/1.1714495
- Yamamoto, Y., Yamada, H. (1982). New analytical expressions for flux distribution and demagnetizing factor of cylindrical core. Electrical Engineering in Japan, 102 (3), 1–8. https://doi.org/10.1002/ecja.4391020302
- Getman, A. V., Konstantinov, A. V. (2013). Cylindrical harmonics of magnetic field of linear magnetized cylinder. Tecnnical Electrodinamics, 1, 3–8. Available at: http://dspace.nbuv.gov.ua/handle/123456789/62253
- Get'man, A. V., Konstantinov, A. V. (2013). Method of cylindrical harmonic analysis of magnetic field of objects with inductive magnetization. Eastern-European Journal of Enterprise Technologies, 3 (5 (63), 3–8. Available at: https://journals.uran.ua/eejet/article/view/14463
- Chen, D.-X., Brug, J. A., Goldfarb, R. B. (1991). Demagnetizing factors for cylinders. IEEE Transactions on Magnetics, 27 (4), 3601–3619. https://doi.org/10.1109/20.102932
- Varga, L. K., Kováč, J., Novák, L. (2020). Determination of external and internal demagnetizing factors for strip-like amorphous ribbon samples. Journal of Magnetism and Magnetic Materials, 507, 166845. https://doi.org/10.1016/j.jmmm.2020.166845
- Kobayashi, M., Ishikawa, Y. (1992). Surface magnetic charge distributions and demagnetizing factors of circular cylinders. IEEE Transactions on Magnetics, 28 (3), 1810–1814. https://doi.org/10.1109/20.141290
- Etse, K., Mininger, X. (2022). Determination of demagnetizing factors for various geometries using an iterative numerical approach. Journal of Magnetism and Magnetic Materials, 564, 170151. https://doi.org/10.1016/j.jmmm.2022.170151
- Chadebec, O., Rouve, L.-L., Coulomb, J.-L. (2002). New methods for a fast and easy computation of stray fields created by wound rods. IEEE Transactions on Magnetics, 38 (2), 517–520. https://doi.org/10.1109/20.996136
- Chen, D.-X., Pardo, E., Sanchez, A. (2006). Fluxmetric and magnetometric demagnetizing factors for cylinders. Journal of Magnetism and Magnetic Materials, 306 (1), 135–146. https://doi.org/10.1016/j.jmmm.2006.02.235
- Prozorov, R., Kogan, V. G. (2018). Effective Demagnetizing Factors of Diamagnetic Samples of Various Shapes. Physical Review Applied, 10 (1). https://doi.org/10.1103/physrevapplied.10.014030
- Maxwell, J. C. (1998). A Treatise On Electricity And Magnetism. Oxford University Press. https://doi.org/10.1093/oso/9780198503743.001.0001
- Smythe, W. (1989). Static and Dynamic Electricity. Hemisphere Publishing Corporation, 623.
- Van Bladel, J. G. (2006). Electromagnetic Fields. John Wiley & Sons. https://doi.org/10.1002/047012458x
- Vanderlinde, J. (2005). Classical Electromagnetic Theory. Springer Netherlands. https://doi.org/10.1007/1-4020-2700-1
- Get'man, A. V., Konstantinov, A. V. (2011). Spatial distribution of charged cylindrical surfaces potential. Eastern-European Journal of Enterprise Technologies, 2 (5 (50), 60–62. Available at: https://journals.uran.ua/eejet/article/view/1794
##submission.downloads##
Опубліковано
Як цитувати
Номер
Розділ
Ліцензія
Авторське право (c) 2024 Andriy Getman, Oleksandr Konstantinov

Ця робота ліцензується відповідно до Creative Commons Attribution 4.0 International License.
Закріплення та умови передачі авторських прав (ідентифікація авторства) здійснюється у Ліцензійному договорі. Зокрема, автори залишають за собою право на авторство свого рукопису та передають журналу право першої публікації цієї роботи на умовах ліцензії Creative Commons CC BY. При цьому вони мають право укладати самостійно додаткові угоди, що стосуються неексклюзивного поширення роботи у тому вигляді, в якому вона була опублікована цим журналом, але за умови збереження посилання на першу публікацію статті в цьому журналі.
Ліцензійний договір – це документ, в якому автор гарантує, що володіє усіма авторськими правами на твір (рукопис, статтю, тощо).
Автори, підписуючи Ліцензійний договір з ПП «ТЕХНОЛОГІЧНИЙ ЦЕНТР», мають усі права на подальше використання свого твору за умови посилання на наше видання, в якому твір опублікований. Відповідно до умов Ліцензійного договору, Видавець ПП «ТЕХНОЛОГІЧНИЙ ЦЕНТР» не забирає ваші авторські права та отримує від авторів дозвіл на використання та розповсюдження публікації через світові наукові ресурси (власні електронні ресурси, наукометричні бази даних, репозитарії, бібліотеки тощо).
За відсутності підписаного Ліцензійного договору або за відсутністю вказаних в цьому договорі ідентифікаторів, що дають змогу ідентифікувати особу автора, редакція не має права працювати з рукописом.
Важливо пам’ятати, що існує і інший тип угоди між авторами та видавцями – коли авторські права передаються від авторів до видавця. В такому разі автори втрачають права власності на свій твір та не можуть його використовувати в будь-який спосіб.










