Конструювання сферичних некруглих коліс, утворених симетричними дугами локсодроми
DOI:
https://doi.org/10.15587/1729-4061.2023.272400Ключові слова:
некруглі колеса, кочення, конічна передача, довжина дуги, сферична крива, локсодромаАнотація
Конічні зубчасті передачі використовуються для передачі крутного моменту між осями, що перетинаються. Вони мають високу надійність та довговічність роботи, стале передаточне число. Недоліком такої передачі є взаємне ковзання поверхонь зубців зубчастих коліс, що призводить до виникнення сил тертя і зносу їх робочих поверхонь. У зв’язку з цим постає питання проектування таких конічних передач, у яких було б відсутнє ковзання.
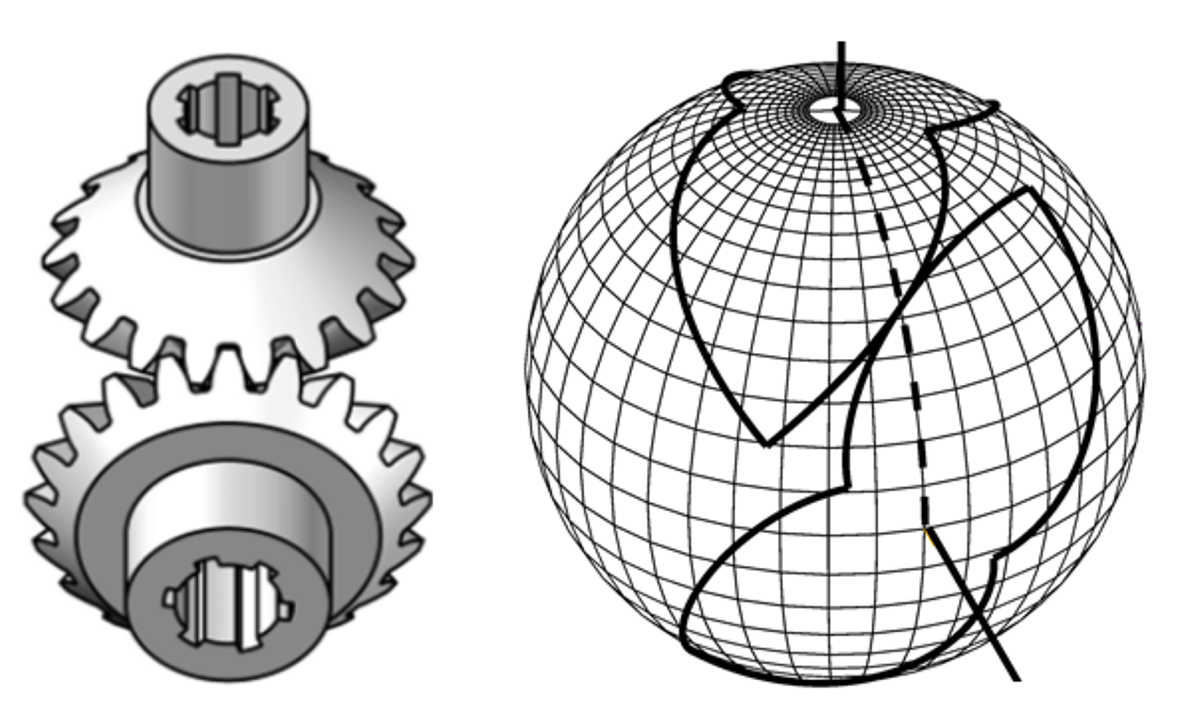
Під некруглими колесами розуміють пару замкнених кривих, які обертаються навколо нерухомих центрів і при цьому перекочуються одна по одній без ковзання. Вони можуть служити центроїдами для проектування циліндричних зубчастих передач між паралельними осями. Якщо осі обертання коліс перетинаються, то передачі називаються конічними. Аналогом передач між паралельними осями, у яких центроїди є плоскими замкненими кривими, для передач із осями, що перетинаються, є сферичні замкнені криві. Для конічної передачі зі сталим передавальним числом такими сферичними кривими є кола на поверхні сфери, а зі змінним передавальним числом – просторові сферичні криві. Розглянуто конструювання замкнених сферичних кривих, які обкочуються одна по одній без ковзання при їх обертанні навколо осей, що перетинаються у центрі сфери. Ці криві утворені із симетричних дуг локсодроми – кривої, яка перетинає всі меридіани кулі під сталим кутом. Цей кут має становити 45°, що забезпечує перетин локсодром під прямим кутом. Отримано аналітичні залежності, на основі яких здійснено розрахунок профілів сферичних некруглих коліс та їх візуалізацію засобами комп’ютерної графіки. Результати можуть бути використані у проектуванні некруглих коліс для текстильних станків, насосів гідромашин, насосів-дозаторів тощо
Посилання
- Konopatskiy, E., Voronova, O., Bezditnyi, A., Shevchuk, O. (2020). About one method of numeral decision of differential equalizations in partials using geometric interpolants. CPT2020 The 8th International Scientific Conference on Computing in Physics and Technology Proceedings. doi: https://doi.org/10.30987/conferencearticle_5fce27708eb353.92843700
- Konopatskiy, E. V., Bezditnyi, A. A. (2020). Geometric modeling of multifactor processes and phenomena by the multidimensional parabolic interpolation method. Journal of Physics: Conference Series, 1441 (1), 012063. doi: https://doi.org/10.1088/1742-6596/1441/1/012063
- Konopatskiy, E., Bezditnyi, A., Shevchuk, O. (2020). Modeling Geometric Varieties with Given Differential Characteristics and Its Application. Proceedings of the 30th International Conference on Computer Graphics and Machine Vision (GraphiCon 2020). Part 2, short31-1-short31-8. doi: https://doi.org/10.51130/graphicon-2020-2-4-31
- Tarelnyk, V., Martsynkovskyy, V., Gaponova, O., Konoplianchenko, I., Dovzyk, M., Tarelnyk, N., Gorovoy, S. (2017). New sulphiding method for steel and cast iron parts. IOP Conference Series: Materials Science and Engineering, 233, 012049. doi: https://doi.org/10.1088/1757-899x/233/1/012049
- Tarelnyk, V., Martsynkovskyy, V., Gaponova, O., Konoplianchenko, I., Belous, A., Gerasimenko, V., Zakharov, M. (2017). New method for strengthening surfaces of heat treated steel parts. IOP Conference Series: Materials Science and Engineering, 233, 012048. doi: https://doi.org/10.1088/1757-899x/233/1/012048
- Tarel’nik, V. B., Martsinkovskii, V. S., Zhukov, A. N. (2017). Increase in the Reliability and Durability of Metal Impulse End Seals. Part 1. Chemical and Petroleum Engineering, 53 (1-2), 114–120. doi: https://doi.org/10.1007/s10556-017-0305-y
- Pylypaka, S. F., Klendii, M. B., Trokhaniak, V. I., Kresan, T. A., Hryshchenko, I. Y., Pastushenko, A. S. (2021). External rolling of a polygon on closed curvilinear profile. Acta Polytechnica, 61 (1), 270–278. doi: https://doi.org/10.14311/ap.2021.61.0270
- Lyashkov, A. A., Panchuk, K. L., Khasanova, I. A. (2018). Automated Geometric and Computer-aided Non-Circular Gear Formation Modeling. Journal of Physics: Conference Series, 1050, 012049. doi: https://doi.org/10.1088/1742-6596/1050/1/012049
- Lyashkov, A. A., Reinhard, A. J., Murashev, G. E. (2019). Geometric And Computer Modeling of Forming the Gear Wheels with Elliptical Centroid. Journal of Physics: Conference Series, 1260 (11), 112018. doi: https://doi.org/10.1088/1742-6596/1260/11/112018
- Lin, C., Wu, X. (2018). Calculation and Characteristic Analysis of Tooth Width of Eccentric Helical Curve-Face Gear. Iranian Journal of Science and Technology, Transactions of Mechanical Engineering, 43 (4), 781–797. doi: https://doi.org/10.1007/s40997-018-0239-9
- Liu, J.-G., Tong, Z.-P., Yu, G.-H., Zhao, X., Zhou, H.-L. (2022). Design and Application of Non-Circular Gear with Cusp Pitch Curve. Machines, 10 (11), 985. doi: https://doi.org/10.3390/machines10110985
- Bogdan-Roth, M., Romanet, M., Ripeanu, R. G. (2019). Device for machining non-circular gears. Proceedings on Engineering Sciences, 1 (1), 449–453. doi: https://doi.org/10.24874/pes01.01.059
- Kalchenko, V., Kalchenko, V., Kolohoida, A., Yeroshenko, A., Kalchenko, D. (2022). Building a model of dressing the working surfaces of wheels during the two-side grinding of round end faces at CNC machines. Eastern-European Journal of Enterprise Technologies, 1 (1 (115)), 86–93. doi: https://doi.org/10.15587/1729-4061.2022.252642
- Krawiec, P., Czarnecka-Komorowska, D., Warguła, Ł., Wojciechowski, S. (2021). Geometric Specification of Non-Circular Pulleys Made with Various Additive Manufacturing Techniques. Materials, 14 (7), 1682. doi: https://doi.org/10.3390/ma14071682
##submission.downloads##
Опубліковано
Як цитувати
Номер
Розділ
Ліцензія
Авторське право (c) 2023 Tetiana Kresan, Ali Kadhim Ahmed, Serhii Pylypaka, Tatiana Volina, Svіtlana Semirnenko, Viktor Trokhaniak, Irina Zakharova

Ця робота ліцензується відповідно до Creative Commons Attribution 4.0 International License.
Закріплення та умови передачі авторських прав (ідентифікація авторства) здійснюється у Ліцензійному договорі. Зокрема, автори залишають за собою право на авторство свого рукопису та передають журналу право першої публікації цієї роботи на умовах ліцензії Creative Commons CC BY. При цьому вони мають право укладати самостійно додаткові угоди, що стосуються неексклюзивного поширення роботи у тому вигляді, в якому вона була опублікована цим журналом, але за умови збереження посилання на першу публікацію статті в цьому журналі.
Ліцензійний договір – це документ, в якому автор гарантує, що володіє усіма авторськими правами на твір (рукопис, статтю, тощо).
Автори, підписуючи Ліцензійний договір з ПП «ТЕХНОЛОГІЧНИЙ ЦЕНТР», мають усі права на подальше використання свого твору за умови посилання на наше видання, в якому твір опублікований. Відповідно до умов Ліцензійного договору, Видавець ПП «ТЕХНОЛОГІЧНИЙ ЦЕНТР» не забирає ваші авторські права та отримує від авторів дозвіл на використання та розповсюдження публікації через світові наукові ресурси (власні електронні ресурси, наукометричні бази даних, репозитарії, бібліотеки тощо).
За відсутності підписаного Ліцензійного договору або за відсутністю вказаних в цьому договорі ідентифікаторів, що дають змогу ідентифікувати особу автора, редакція не має права працювати з рукописом.
Важливо пам’ятати, що існує і інший тип угоди між авторами та видавцями – коли авторські права передаються від авторів до видавця. В такому разі автори втрачають права власності на свій твір та не можуть його використовувати в будь-який спосіб.









