Unbalanced credit fraud modeling based on bagging and bayesian optimization
DOI:
https://doi.org/10.15587/1729-4061.2023.279936Keywords:
unbalanced data, Bayesian optimization, random forest, majority and minority classAbstract
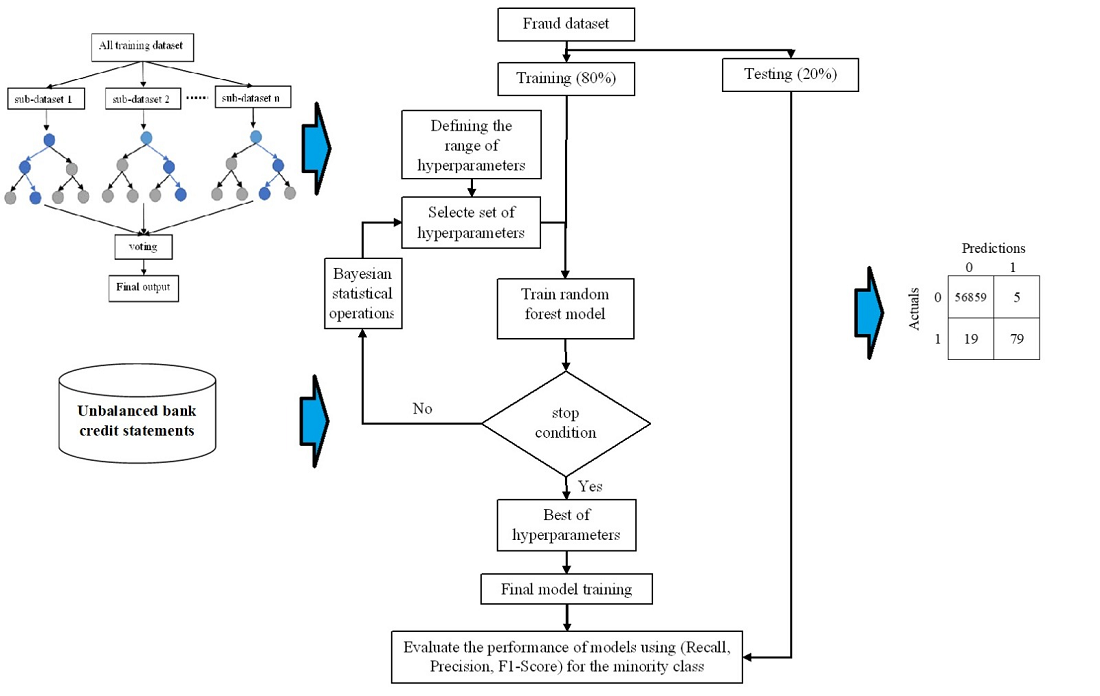
Credit fraud modeling is a crucial area of research that is highly relevant to the credit loan industry. Effective risk management is a key factor in providing quality credit services and directly impacts the profitability and bad debt ratio of leading organizations in this sector. However, when the distribution of credit fraud data is highly unbalanced, it can lead to noise errors caused by information distortion, periodic statistical errors, and model biases during training. This can cause unfair results for the minority class (target class) and increase the risk of overfitting. While traditional data balancing methods can reduce bias in models towards the majority class in relatively unbalanced data, they may not be effective in highly unbalanced scenarios. To address this challenge, this paper proposes using Bagging algorithms such as Random Forest and Bagging to model highly unbalanced credit fraud data. Bayesian optimization is utilized to find hyperparameters and determine the accuracy of the minority class as an optimization function for the model, which is tested with real European credit card fraud data. The results of the proposed packing algorithms are compared with traditional data balancing methods such as Balanced Bagging and Balanced Random Forest. The study found that traditional data balancing methods may not be compatible with excessively unbalanced data, whereas Bagging algorithms show promise as a solution for modeling such data. The proposed method for finding hyperparameters effectively deals with highly unbalanced data. It achieved precision, recall, and F1-score for the minority category of 0.94, 0.81, and 0.87, respectively. The study emphasizes the importance of addressing the challenges associated with unbalanced credit fraud data to improve the accuracy and fairness of credit fraud models
Supporting Agency
- The authors acknowledge University of Al-Hamdaniya for making laboratories and experimental materials available for this research project.
References
- Patil, Dr. A. (2018). Digital Transformation in Financial Services and Challenges and Opportunities. International Journal of Trend in Scientific Research and Development, Special Issue (Special Issue-ICDEBI2018), 10–12. doi: https://doi.org/10.31142/ijtsrd18661
- McNulty, D., Milne, A. (2021). Bigger Fish to Fry: FinTech and the Digital Transformation of Financial Services. Disruptive Technology in Banking and Finance, 263–281. doi: https://doi.org/10.1007/978-3-030-81835-7_10
- Lokanan, M. E., Sharma, K. (2022). Fraud prediction using machine learning: The case of investment advisors in Canada. Machine Learning with Applications, 8, 100269. doi: https://doi.org/10.1016/j.mlwa.2022.100269
- Roberts, P. (2022). Risk Management Systems. Simplifying Risk Management, 43–66. doi: https://doi.org/10.4324/9781003225157-3
- Meng, C., Zhou, L., Liu, B. (2020). A Case Study in Credit Fraud Detection With SMOTE and XGBoost. Journal of Physics: Conference Series, 1601 (5), 052016. doi: https://doi.org/10.1088/1742-6596/1601/5/052016
- Lin, T.-H., Jiang, J.-R. (2021). Credit Card Fraud Detection with Autoencoder and Probabilistic Random Forest. Mathematics, 9 (21), 2683. doi: https://doi.org/10.3390/math9212683
- Shamsudin, H., Yusof, U. K., Jayalakshmi, A., Akmal Khalid, M. N. (2020). Combining oversampling and undersampling techniques for imbalanced classification: A comparative study using credit card fraudulent transaction dataset. 2020 IEEE 16th International Conference on Control & Automation (ICCA). doi: https://doi.org/10.1109/icca51439.2020.9264517
- Ahammad, J., Hossain, N., Alam, M. S. (2020). Credit Card Fraud Detection using Data Pre-processing on Imbalanced Data - both Oversampling and Undersampling. Proceedings of the International Conference on Computing Advancements. doi: https://doi.org/10.1145/3377049.3377113
- Praveen Mahesh, K., Ashar Afrouz, S., Shaju Areeckal, A. (2022). Detection of fraudulent credit card transactions: A comparative analysis of data sampling and classification techniques. Journal of Physics: Conference Series, 2161 (1), 012072. doi: https://doi.org/10.1088/1742-6596/2161/1/012072
- Wang, S., Dai, Y., Shen, J., Xuan, J. (2021). Research on expansion and classification of imbalanced data based on SMOTE algorithm. Scientific Reports, 11 (1). doi: https://doi.org/10.1038/s41598-021-03430-5
- Klikowski, J Woźniak, M. (2022). Deterministic Sampling Classifier with weighted Bagging for drifted imbalanced data stream classification. Applied Soft Computing, 122, 108855. doi: https://doi.org/10.1016/j.asoc.2022.108855
- Kim, M., Hwang, K.-B. (2022). An empirical evaluation of sampling methods for the classification of imbalanced data. PLOS ONE, 17 (7), e0271260. doi: https://doi.org/10.1371/journal.pone.0271260
- Liu, Z., Cao, W., Gao, Z., Bian, J., Chen, H., Chang, Y., Liu, T.-Y. (2020). Self-paced Ensemble for Highly Imbalanced Massive Data Classification. 2020 IEEE 36th International Conference on Data Engineering (ICDE). doi: https://doi.org/10.1109/icde48307.2020.00078
- Park, S., Lee, H.-W., Im, J. (2022). Resampling-Based Relabeling & Raking Algorithm to One-Class Classification. doi: https://doi.org/10.36227/techrxiv.17712122.v2
- Juez-Gil, M., Arnaiz-González, Á., Rodríguez, J. J., García-Osorio, C. (2021). Experimental evaluation of ensemble classifiers for imbalance in Big Data. Applied Soft Computing, 108, 107447. doi: https://doi.org/10.1016/j.asoc.2021.107447
- Wang, Q., Luo, Z., Huang, J., Feng, Y., Liu, Z. (2017). A Novel Ensemble Method for Imbalanced Data Learning: Bagging of Extrapolation-SMOTE SVM. Computational Intelligence and Neuroscience, 2017, 1–11. doi: https://doi.org/10.1155/2017/1827016
- Singh, G., Chu, L., Wang, L., Pei, J., Tian, Q., Zhang, Y. (2022). Mining Minority-Class Examples with Uncertainty Estimates. Lecture Notes in Computer Science, 258–271. doi: https://doi.org/10.1007/978-3-030-98358-1_21
- Rayhan, F., Ahmed, S., Mahbub, A., Jani, Md. R., Shatabda, S., Farid, D. Md., Rahman, C. M. (2017). MEBoost: Mixing estimators with boosting for imbalanced data classification. 2017 11th International Conference on Software, Knowledge, Information Management and Applications (SKIMA). doi: https://doi.org/10.1109/skima.2017.8294128
- Meng, Q. (2022). Credit Card Fraud Detection Using Feature Fusion-based Machine Learning Model. Highlights in Science, Engineering and Technology, 23, 111–116. doi: https://doi.org/10.54097/hset.v23i.3208
- Zhou, Z.-H. (2020). Ensemble Learning: Foundations and Algorithms. Beijing: Electronic Industry Press.
- Chen, Z., Duan, J., Kang, L., Qiu, G. (2021). A hybrid data-level ensemble to enable learning from highly imbalanced dataset. Information Sciences, 554, 157–176. doi: https://doi.org/10.1016/j.ins.2020.12.023
- Bader-El-Den, M., Teitei, E., Perry, T. (2019). Biased Random Forest For Dealing With the Class Imbalance Problem. IEEE Transactions on Neural Networks and Learning Systems, 30 (7), 2163–2172. doi: https://doi.org/10.1109/tnnls.2018.2878400
- Borah, P., Gupta, D. (2021). Robust twin bounded support vector machines for outliers and imbalanced data. Applied Intelligence, 51 (8), 5314–5343. doi: https://doi.org/10.1007/s10489-020-01847-5
- Gupta, D., Richhariya, B. (2018). Entropy based fuzzy least squares twin support vector machine for class imbalance learning. Applied Intelligence, 48 (11), 4212–4231. doi: https://doi.org/10.1007/s10489-018-1204-4
- Husejinovic, A. (2020). Credit card fraud detection using naive Bayesian and C4.5 decision tree classifiers. Periodicals of Engineering and Natural Sciences, 8 (1), 1–5.
- Kalid, S. N., Ng, K.-H., Tong, G.-K., Khor, K.-C. (2020). A Multiple Classifiers System for Anomaly Detection in Credit Card Data With Unbalanced and Overlapped Classes. IEEE Access, 8, 28210–28221. doi: https://doi.org/10.1109/access.2020.2972009
- Lee, T.-H., Ullah, A., Wang, R. (2019). Bootstrap Aggregating and Random Forest. Advanced Studies in Theoretical and Applied Econometrics, 389–429. doi: https://doi.org/10.1007/978-3-030-31150-6_13
- Denuit, M., Hainaut, D., Trufin, J. (2020). Bagging Trees and Random Forests. Effective Statistical Learning Methods for Actuaries II, 107–130. doi: https://doi.org/10.1007/978-3-030-57556-4_4
- Genuer, R., Poggi, J.-M. (2020). Random Forests. Random Forests with R, 33–55. doi: https://doi.org/10.1007/978-3-030-56485-8_3
- Syam, N., Kaul, R. (2021). Random Forest, Bagging, and Boosting of Decision Trees. Machine Learning and Artificial Intelligence in Marketing and Sales, 139–182. doi: https://doi.org/10.1108/978-1-80043-880-420211006
- Breiman, L. (2001). Random Forests. Machine Learning, 45, 5–32. doi: https://doi.org/10.1023/a:1010933404324
- Hatwell, J., Gaber, M. M., Azad, R. M. A. (2020). CHIRPS: Explaining random forest classification. Artificial Intelligence Review, 53 (8), 5747–5788. doi: https://doi.org/10.1007/s10462-020-09833-6
- Lin, W., Gao, J., Wang, B., Hong, Q. (2021). An Improved Random Forest Classifier for Imbalanced Learning. 2021 IEEE International Conference on Artificial Intelligence and Computer Applications (ICAICA). doi: https://doi.org/10.1109/icaica52286.2021.9497933
- Sudha, C., Akila, D. (2021). Credit Card Fraud Detection System based on Operational & Transaction features using SVM and Random Forest Classifiers. 2021 2nd International Conference on Computation, Automation and Knowledge Management (ICCAKM). doi: https://doi.org/10.1109/iccakm50778.2021.9357709
- Aung, M. H., Seluka, P. T., Fuata, J. T. R., Tikoisuva, M. J., Cabealawa, M. S., Nand, R. (2020). Random Forest Classifier for Detecting Credit Card Fraud based on Performance Metrics. 2020 IEEE Asia-Pacific Conference on Computer Science and Data Engineering (CSDE). doi: https://doi.org/10.1109/csde50874.2020.9411563
- Credit Card Fraud Detection. Available at: https://www.kaggle.com/datasets/mlg-ulb/creditcardfraud
- Carrington, A. M., Manuel, D. G., Fieguth, P. W., Ramsay, T., Osmani, V., Wernly, B. et al. (2023). Deep ROC Analysis and AUC as Balanced Average Accuracy, for Improved Classifier Selection, Audit and Explanation. IEEE Transactions on Pattern Analysis and Machine Intelligence, 45 (1), 329–341. doi: https://doi.org/10.1109/tpami.2022.3145392
- Kamble, S., Desai, A., Vartak, P. (2014). Evaluation and Performance Analysis of Machine Learning Algorithms. International Journal of Engineering Sciences & Research Technology, 3 (5), 789–794.
- Glisic, S. G., Lorenzo, B. (2022). Machine Learning Algorithms. Artificial Intelligence and Quantum Computing for Advanced Wireless Networks, 17–54. doi: https://doi.org/10.1002/9781119790327.ch2
- Piegorsch, W. W. (2020). Confusion Matrix. Wiley StatsRef: Statistics Reference Online, 1–4. doi: https://doi.org/10.1002/9781118445112.stat08244
Downloads
Published
How to Cite
Issue
Section
License
Copyright (c) 2023 Mohammed Alaaalden Kashmoola, Samah Fakhri Aziz, Hasan Mudhafar Qays, Naors Y. Anad Alsaleem

This work is licensed under a Creative Commons Attribution 4.0 International License.
The consolidation and conditions for the transfer of copyright (identification of authorship) is carried out in the License Agreement. In particular, the authors reserve the right to the authorship of their manuscript and transfer the first publication of this work to the journal under the terms of the Creative Commons CC BY license. At the same time, they have the right to conclude on their own additional agreements concerning the non-exclusive distribution of the work in the form in which it was published by this journal, but provided that the link to the first publication of the article in this journal is preserved.
A license agreement is a document in which the author warrants that he/she owns all copyright for the work (manuscript, article, etc.).
The authors, signing the License Agreement with TECHNOLOGY CENTER PC, have all rights to the further use of their work, provided that they link to our edition in which the work was published.
According to the terms of the License Agreement, the Publisher TECHNOLOGY CENTER PC does not take away your copyrights and receives permission from the authors to use and dissemination of the publication through the world's scientific resources (own electronic resources, scientometric databases, repositories, libraries, etc.).
In the absence of a signed License Agreement or in the absence of this agreement of identifiers allowing to identify the identity of the author, the editors have no right to work with the manuscript.
It is important to remember that there is another type of agreement between authors and publishers – when copyright is transferred from the authors to the publisher. In this case, the authors lose ownership of their work and may not use it in any way.








